广西河池市2020年中考数学试卷
试卷更新日期:2020-08-24 类型:中考真卷
一、选择题(共12小题).
-
1. 如果收入10元记作+10元,那么支出10元记作( )A、+20 元 B、+10元 C、-10元 D、-20元2. 如图,直线a,b被直线c所截,则∠1与∠2的位置关系是( )
 A、同位角 B、内错角 C、同旁内角 D、邻补角3. 若 有意义,则x的取值范围是( )A、x>0 B、x≥0 C、x>2 D、x≥24. 下列运算,正确的是( )A、 B、 C、2a-a=1 D、a2+a=3a5. 下列立体图形中,主视图为矩形的是( )A、
A、同位角 B、内错角 C、同旁内角 D、邻补角3. 若 有意义,则x的取值范围是( )A、x>0 B、x≥0 C、x>2 D、x≥24. 下列运算,正确的是( )A、 B、 C、2a-a=1 D、a2+a=3a5. 下列立体图形中,主视图为矩形的是( )A、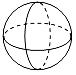 B、
B、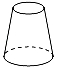 C、
C、 D、
D、 6. 不等式组 的解集在数轴上表示正确的是( )A、
6. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、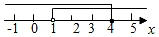 7. 在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是( )A、 B、 C、 D、8. 某学习小组7名同学的《数据的分析》一章的测验成绩如下(单位:分)85,90,89,85,98,88,80,则该组数据的众数、中位数分别是( )A、85,85 B、85,88 C、88,85 D、88,889. 观察下列作图痕迹,所作CD为△ABC的边AB上的中线是( )A、
7. 在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是( )A、 B、 C、 D、8. 某学习小组7名同学的《数据的分析》一章的测验成绩如下(单位:分)85,90,89,85,98,88,80,则该组数据的众数、中位数分别是( )A、85,85 B、85,88 C、88,85 D、88,889. 观察下列作图痕迹,所作CD为△ABC的边AB上的中线是( )A、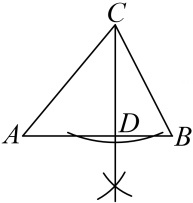 B、
B、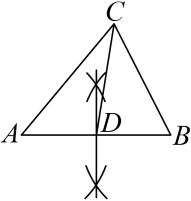 C、
C、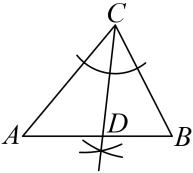 D、
D、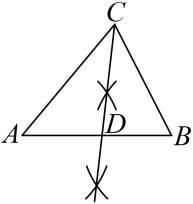 10. 某年级举办篮球友谊赛,参赛的每两个队之间都要比赛一场,共要比赛36场,则参加此次比赛的球队数是( )A、6 B、7 C、8 D、911. 如图,在 中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4.则CE的长是( )
10. 某年级举办篮球友谊赛,参赛的每两个队之间都要比赛一场,共要比赛36场,则参加此次比赛的球队数是( )A、6 B、7 C、8 D、911. 如图,在 中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4.则CE的长是( ) A、5 B、6 C、4 D、512. 如图,AB是 O的直径,CD是弦,AE⊥CD于点E,BF⊥CD于点F.若BF=FE=2,FC=1,则AC的长是( )
A、5 B、6 C、4 D、512. 如图,AB是 O的直径,CD是弦,AE⊥CD于点E,BF⊥CD于点F.若BF=FE=2,FC=1,则AC的长是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(共6小题).
-
13. 计算:3-(-2)=.14. 方程 的解是x-.15. 如图,菱形ABCD的周长为16,AC,BD交于点O,点E在BC上,OE∥AB,则OE的长是.
 16. 不透明的袋子中装有红、蓝小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到相同颜色的小球的概率是.17. 如图,AB是 的直径,点C,D,E都在 上,∠1=55°,则∠2=°
16. 不透明的袋子中装有红、蓝小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到相同颜色的小球的概率是.17. 如图,AB是 的直径,点C,D,E都在 上,∠1=55°,则∠2=°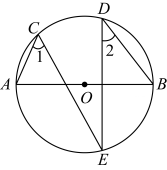 18. 如图,在Rt△ABC中,∠B=90°,∠A=30°,AC=8,点D在AB上,且 ,点E在BC上运动.将△BDE沿DE折叠,点B落在点 处,则点 到AC的最短距离是.
18. 如图,在Rt△ABC中,∠B=90°,∠A=30°,AC=8,点D在AB上,且 ,点E在BC上运动.将△BDE沿DE折叠,点B落在点 处,则点 到AC的最短距离是.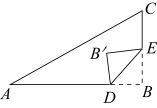
三、解答题(本大题共8小题,共66分.)
-
19. 计算: .20. 先化简,再计算: ,其中a=2.21. 如图,在平面直角坐标系xOy中,A(-1,2).
 (1)、将点A向右平移3个单位长度,再向上平移1个单位长度,得到点B,则点B的坐标是.(2)、点C与点A关于原点O对称,则点C的坐标是.(3)、反比例函数的图象经过点B,则它的解析式是.(4)、一次函数的图象经过A,C两点,则它的解析式是.22. 如图
(1)、将点A向右平移3个单位长度,再向上平移1个单位长度,得到点B,则点B的坐标是.(2)、点C与点A关于原点O对称,则点C的坐标是.(3)、反比例函数的图象经过点B,则它的解析式是.(4)、一次函数的图象经过A,C两点,则它的解析式是.22. 如图 (1)、如图(1),已知CE与AB交于点E,AC=BC,∠1=∠2.求证: .(2)、如图(2),已知CD的延长线与AB交于点E,AD=BC,∠3=∠4.探究AE与BE的数量关系,并说明理由.23. 某校举行了主题为“防溺水,保安全”的知识竞赛活动.赛后随机抽取了50名参赛学生的成绩进行相关统计,整理得尚未完整的频数分布表和扇形统计图.现累计了40名参赛学生的成绩,余下10名参赛学生的成绩尚未累计,这10名学生成绩如下(单位:分)75,63,76,87,69,78,82,75,63,71.
(1)、如图(1),已知CE与AB交于点E,AC=BC,∠1=∠2.求证: .(2)、如图(2),已知CD的延长线与AB交于点E,AD=BC,∠3=∠4.探究AE与BE的数量关系,并说明理由.23. 某校举行了主题为“防溺水,保安全”的知识竞赛活动.赛后随机抽取了50名参赛学生的成绩进行相关统计,整理得尚未完整的频数分布表和扇形统计图.现累计了40名参赛学生的成绩,余下10名参赛学生的成绩尚未累计,这10名学生成绩如下(单位:分)75,63,76,87,69,78,82,75,63,71.频数分布表
组别
分数段
划记
频数
A
60<x≤70
正
B
70<x≤80
正正
C
80<x≤90
正正正正
D
90<x≤100
正
 (1)、在频数分布表中补全各组划记和频数;(2)、求扇形统计图中B组所对应的圆心角的度数;(3)、该校有2000名学生参加此次知识竞赛,估计成绩在80<x≤100的学生有多少人?24. 某水果市场销售一种香蕉.甲店的香蕉价格为4元/kg;乙店的香蕉价格为5元/kg,若一次购买6kg以上,超过6kg部分的价格打7折.(1)、设购买香蕉xkg,付款金额y元,分别就两店的付款金额写出y关于x的函数解析式;(2)、到哪家店购买香蕉更省钱?请说明理由.25. 如图,AB是 的直径,AB=6,OC⊥AB,OC=5,BC与 交于点D,点E是 的中点,EF∥BC,交OC的延长线于点F.
(1)、在频数分布表中补全各组划记和频数;(2)、求扇形统计图中B组所对应的圆心角的度数;(3)、该校有2000名学生参加此次知识竞赛,估计成绩在80<x≤100的学生有多少人?24. 某水果市场销售一种香蕉.甲店的香蕉价格为4元/kg;乙店的香蕉价格为5元/kg,若一次购买6kg以上,超过6kg部分的价格打7折.(1)、设购买香蕉xkg,付款金额y元,分别就两店的付款金额写出y关于x的函数解析式;(2)、到哪家店购买香蕉更省钱?请说明理由.25. 如图,AB是 的直径,AB=6,OC⊥AB,OC=5,BC与 交于点D,点E是 的中点,EF∥BC,交OC的延长线于点F. (1)、求证:EF是 的切线;(2)、CG∥OD,交AB于点G,求CG的长.26. 在平面直角坐标系xOy中,抛物线与x轴交于(p,0),(q,0),则该抛物线的解析式可以表示为:
(1)、求证:EF是 的切线;(2)、CG∥OD,交AB于点G,求CG的长.26. 在平面直角坐标系xOy中,抛物线与x轴交于(p,0),(q,0),则该抛物线的解析式可以表示为:y=a(x-p)(x-q),
=ax2-a(p+q)x+apq.
 (1)、若a=1,抛物线与x轴交于(1,0),(5,0),直接写出该抛物线的解析式和顶点坐标;(2)、若a=-1,如图(1),A(-1,0),B(3,0),点M(m,0)在线段AB上,抛物线C1与x轴交于A,M,顶点为C;抛物线C2与x轴交于B,M,顶点为D.当A,C,D三点在同一条直线上时,求m的值;(3)、已知抛物线C3与x轴交于A(-1,0),B(3,0),线段EF的端点E(0,3),F(4,3).若抛物线C3与线段EF有公共点,结合图象,在图(2)中探究a的取值范围.
(1)、若a=1,抛物线与x轴交于(1,0),(5,0),直接写出该抛物线的解析式和顶点坐标;(2)、若a=-1,如图(1),A(-1,0),B(3,0),点M(m,0)在线段AB上,抛物线C1与x轴交于A,M,顶点为C;抛物线C2与x轴交于B,M,顶点为D.当A,C,D三点在同一条直线上时,求m的值;(3)、已知抛物线C3与x轴交于A(-1,0),B(3,0),线段EF的端点E(0,3),F(4,3).若抛物线C3与线段EF有公共点,结合图象,在图(2)中探究a的取值范围.