辽宁省铁岭、葫芦岛市2020年中考数学试卷
试卷更新日期:2020-08-24 类型:中考真卷
一、选择题
-
1. 的绝对值是( )A、3 B、-3 C、 D、2. 下图是由5个完全相同的小正方体组成的立体图形,它的俯视图是( )
 A、
A、 B、
B、 C、
C、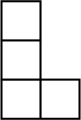 D、
D、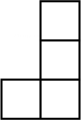 3. 下列运算正确的是( )A、 B、 C、 D、4. 一组数据1,4,3,1,7,5的众数是( )A、1 B、2 C、2.5 D、3.55. 一个不透明的口袋中有4个红球、2个白球,这些球除颜色外无其他差别,从袋子中随机摸出1个球,则摸到红球的概率是( )A、 B、 C、 D、6. 不等式组 的整数解的个数是( )A、2 B、3 C、4 D、57. 我市在落实国家“精准扶贫”政策的过程中,为某村修建一条长为400米的公路,由甲、乙两个工程队负责施工.甲工程队独立施工2天后,乙工程队加入两工程队联合施工3天后,还剩50米的工程.已知甲工程队每天比乙工程队多施工2米,求甲、乙工程队每天各施工多少米?设甲工程队每天施工 米,乙工程队每天施工 米,根据题意,所列方程组正确的是( )A、 B、 C、 D、8. 一个零件的形状如图所示, ,则 的度数是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 一组数据1,4,3,1,7,5的众数是( )A、1 B、2 C、2.5 D、3.55. 一个不透明的口袋中有4个红球、2个白球,这些球除颜色外无其他差别,从袋子中随机摸出1个球,则摸到红球的概率是( )A、 B、 C、 D、6. 不等式组 的整数解的个数是( )A、2 B、3 C、4 D、57. 我市在落实国家“精准扶贫”政策的过程中,为某村修建一条长为400米的公路,由甲、乙两个工程队负责施工.甲工程队独立施工2天后,乙工程队加入两工程队联合施工3天后,还剩50米的工程.已知甲工程队每天比乙工程队多施工2米,求甲、乙工程队每天各施工多少米?设甲工程队每天施工 米,乙工程队每天施工 米,根据题意,所列方程组正确的是( )A、 B、 C、 D、8. 一个零件的形状如图所示, ,则 的度数是( )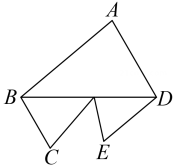 A、70° B、80° C、90° D、100°9. 如图,矩形 的顶点 在反比例函数 的图象上,点 和点 在 边上, ,连接 轴,则 的值为( )
A、70° B、80° C、90° D、100°9. 如图,矩形 的顶点 在反比例函数 的图象上,点 和点 在 边上, ,连接 轴,则 的值为( )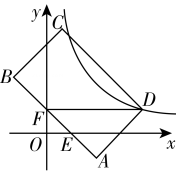 A、 B、3 C、4 D、10. 如图,二次函数 的图象的对称轴是直线 ,则以下四个结论中:① ,② ,③ ,④ .正确的个数是( )
A、 B、3 C、4 D、10. 如图,二次函数 的图象的对称轴是直线 ,则以下四个结论中:① ,② ,③ ,④ .正确的个数是( )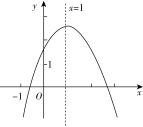 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 伴随“互联网+”时代的来临,预计到2025年,我国各类网络互助平台的实际参与人数将达到450000000人,将数据450000000科学记数法表示为.12. 分解因式: =.13. 甲、乙两人参加“环保知识”竞赛,经过6轮比赛,他们的平均成绩都是97分.如果甲、乙两人比赛成绩的方差分别为 ,则这6次比赛成绩比较稳定的是.(填“甲”或“乙”)14. 已知关于 的一元二次方程 有两个不相等的实数根,则实数 的取值范围是.15. 如图,在 中, ,以 为圆心,以适当的长为半径作弧,交 于点 ,交 于点 ,分别以 为圆心,以大于 的长为半径作弧,两弧在 的内部相交于点 ,作射线 ,交 于点 ,点 在 边上, ,连接 ,则 的周长为.
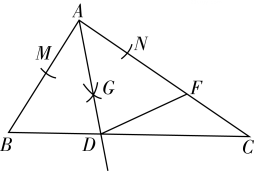 16. 如图,以 为边,在 的同侧分别作正五边形 和等边 ,连接 ,则 的度数是.
16. 如图,以 为边,在 的同侧分别作正五边形 和等边 ,连接 ,则 的度数是. 17. 一张菱形纸片 的边长为 ,高 等于边长的一半,将菱形纸片沿直线 折叠,使点 与点 重合,直线 交直线 于点 ,则 的长为 .18. 如图, ,正方形 ,正方形 ,正方形 ,正方形 ,…,的顶点 ,在射线 上,顶点 ,在射线 上,连接 交 于点 ,连接 交 于点 ,连接 交 于点 ,…,连接 交 于点 ,连接 交 于点 ,…,按照这个规律进行下去,设 与 的面积之和为 与 的面积之和为 与 的面积之和为 ,…,若 ,则 等于.(用含有正整数 的式子表示)
17. 一张菱形纸片 的边长为 ,高 等于边长的一半,将菱形纸片沿直线 折叠,使点 与点 重合,直线 交直线 于点 ,则 的长为 .18. 如图, ,正方形 ,正方形 ,正方形 ,正方形 ,…,的顶点 ,在射线 上,顶点 ,在射线 上,连接 交 于点 ,连接 交 于点 ,连接 交 于点 ,…,连接 交 于点 ,连接 交 于点 ,…,按照这个规律进行下去,设 与 的面积之和为 与 的面积之和为 与 的面积之和为 ,…,若 ,则 等于.(用含有正整数 的式子表示)
三、解答题
-
19. 先化简,再求值: ,其中 .20. 某校计划组建航模、摄影、乐器、舞蹈四个课外活动小组,要求每名同学必须参加,并且只能选择其中一个小组.为了解学生对四个课外活动小组的选择情况,学校从全体学生中随机抽取部分学生进行问卷调查,并把此次调查结果整理并绘制成如下两幅不完整的统计图.

根据图中提供的信息,解答下列问题:
(1)、本次被调查的学生有人;(2)、请补全条形统计图,并求出扇形统计图中“航模”所对应的圆心角的度数;(3)、通过了解,喜爱“航模”的学生中有2名男生和2名女生曾在市航模比赛中获奖,现从这4个人中随机选取2人参加省青少年航模比赛,请用列表或画树状图的方法求出所选的2人恰好是1名男生和1名女生的概率.21. 某中学为了创设“书香校园”,准备购买 两种书架,用于放置图书.在购买时发现, 种书架的单价比 种书架的单价多20元,用600元购买 种书架的个数与用480元购买 种书架的个数相同.(1)、求 两种书架的单价各是多少元?(2)、学校准备购买 两种书架共15个,且购买的总费用不超过1400元,求最多可以购买多少个 种书架?22. 如图,小明利用学到的数学知识测量大桥主架在水面以上的高度 ,在观测点 处测得大桥主架顶端 的仰角为30°,测得大桥主架与水面交汇点 的俯角为14°,观测点与大桥主架的水平距离 为60米,且 垂直于桥面.(点 在同一平面内)
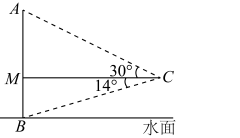
(参考数据 )
(1)、求大桥主架在桥面以上的高度AM;(结果保留根号)(2)、求大桥主架在水面以上的高度 .(结果精确到1米)23. 小红经营的网店以销售文具为主,其中一款笔记本进价为每本10元,该网店在试销售期间发现,每周销售数量 (本)与销售单价 (元)之间满足一次函数关系,三对对应值如下表:销售单价 (元)
12
14
16
每周的销售量 (本)
500
400
300
(1)、求 与 之间的函数关系式;(2)、通过与其他网店对比,小红将这款笔记本的单价定为 元( ,且 为整数),设每周销售该款笔记本所获利润为 元,当销售单价定为多少元时每周所获利润最大,最大利润是多少元?24. 如图,四边形 内接于 是直径, ,连接 ,过点 的直线与 的延长线相交于点 ,且 .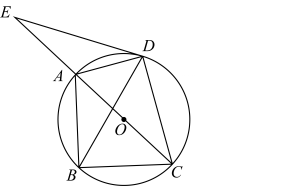 (1)、求证:直线 是 的切线;(2)、若 , ,求 的长.25. 在等腰 和等腰 中, , ,将 绕点 逆时针旋转,连接 ,点 为线段 的中点,连接 .
(1)、求证:直线 是 的切线;(2)、若 , ,求 的长.25. 在等腰 和等腰 中, , ,将 绕点 逆时针旋转,连接 ,点 为线段 的中点,连接 . (1)、如图1,当点 旋转到 边上时,请直接写出线段 与 的位置关系和数量关系;(2)、如图2,当点 旋转到 边上时,(1)中的结论是否成立?若成立,请写出证明过程,若不成立,请说明理由.(3)、若 ,在 绕点 逆时针旋转的过程中,当 时,请直接写出线段 的长.26. 如图,抛物线 与 轴相交于点 和点 ,与 轴相交于点 ,作直线 .
(1)、如图1,当点 旋转到 边上时,请直接写出线段 与 的位置关系和数量关系;(2)、如图2,当点 旋转到 边上时,(1)中的结论是否成立?若成立,请写出证明过程,若不成立,请说明理由.(3)、若 ,在 绕点 逆时针旋转的过程中,当 时,请直接写出线段 的长.26. 如图,抛物线 与 轴相交于点 和点 ,与 轴相交于点 ,作直线 .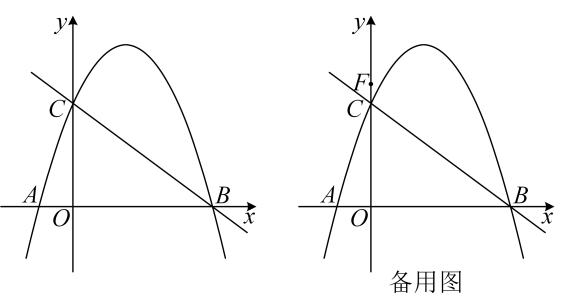 (1)、求抛物线的解析式;(2)、在直线 上方的抛物线上存在点 ,使 ,求点 的坐标;(3)、在(2)的条件下,点 的坐标为 ,点 在抛物线上,点 在直线 上,当以 为顶点的四边形是平行四边形时,请直接写出点 的坐标.
(1)、求抛物线的解析式;(2)、在直线 上方的抛物线上存在点 ,使 ,求点 的坐标;(3)、在(2)的条件下,点 的坐标为 ,点 在抛物线上,点 在直线 上,当以 为顶点的四边形是平行四边形时,请直接写出点 的坐标.