辽宁省阜新市2020年中考数学试卷
试卷更新日期:2020-08-24 类型:中考真卷
一、选择题
-
1. 在实数 ,-1,0,1中,最小的是( )A、 B、-1 C、0 D、12. 下列立体图形中,左视图与主视图不同的是( )A、
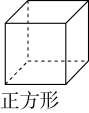 B、
B、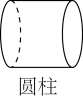 C、
C、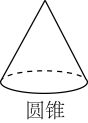 D、
D、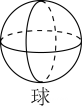 3. 如图,是小明绘制的他在一周内每天跑步圈数的折线统计图.下列结论正确的是( )
3. 如图,是小明绘制的他在一周内每天跑步圈数的折线统计图.下列结论正确的是( )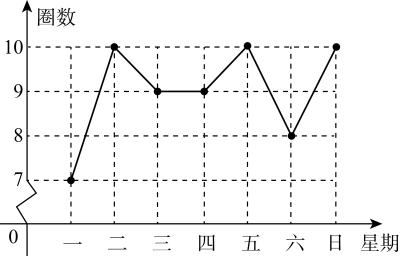 A、众数是9 B、中位数是8.5 C、平均数是9 D、方差是74. 如图, 为⊙ 的直径,C,D是圆周上的两点,若 ,则锐角 的度数为( )
A、众数是9 B、中位数是8.5 C、平均数是9 D、方差是74. 如图, 为⊙ 的直径,C,D是圆周上的两点,若 ,则锐角 的度数为( ) A、57° B、52° C、38° D、26°5. 掷一枚质地均匀的硬币5次,其中3次正面朝上,2次正面朝下,则再次掷出这枚硬币,正面朝下的概率是( )A、1 B、 C、 D、6. 不等式组 的解集,在数轴上表示正确的是( )A、
A、57° B、52° C、38° D、26°5. 掷一枚质地均匀的硬币5次,其中3次正面朝上,2次正面朝下,则再次掷出这枚硬币,正面朝下的概率是( )A、1 B、 C、 D、6. 不等式组 的解集,在数轴上表示正确的是( )A、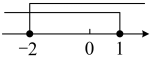 B、
B、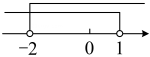 C、
C、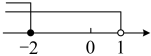 D、
D、 7. 若 与 都是反比例函数 图象上的点,则a的值是( )A、4 B、-4 C、2 D、-28. 在“建设美丽阜新”的行动中,需要铺设一段全长为 的污水排放管道.为了尽量减少施工时对城市交通所造成的影响,实际施工时每天的工效比原计划增加25%,结果提前30天完成这一任务.设实际每天铺 管道,根据题意,所列方程正确的是( )A、 B、 C、 D、9. 已知二次函数 ,则下列关于这个函数图象和性质的说法,正确的是( )A、图象的开口向上 B、图象的顶点坐标是 C、当 时,y随x的增大而增大 D、图象与x轴有唯一交点10. 如图,在平面直角坐标系中,将边长为1的正六边形 绕点O顺时针旋转i个45°,得到正六边形 ,则正六边形 的顶点 的坐标是( )
7. 若 与 都是反比例函数 图象上的点,则a的值是( )A、4 B、-4 C、2 D、-28. 在“建设美丽阜新”的行动中,需要铺设一段全长为 的污水排放管道.为了尽量减少施工时对城市交通所造成的影响,实际施工时每天的工效比原计划增加25%,结果提前30天完成这一任务.设实际每天铺 管道,根据题意,所列方程正确的是( )A、 B、 C、 D、9. 已知二次函数 ,则下列关于这个函数图象和性质的说法,正确的是( )A、图象的开口向上 B、图象的顶点坐标是 C、当 时,y随x的增大而增大 D、图象与x轴有唯一交点10. 如图,在平面直角坐标系中,将边长为1的正六边形 绕点O顺时针旋转i个45°,得到正六边形 ,则正六边形 的顶点 的坐标是( )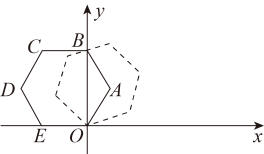 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
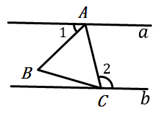
11. 计算: .12. 如图,直线a,b过等边三角形 顶点A和C,且 , ,则 的度数为.
 13. 如图,把 沿 边平移到 的位置,图中所示的三角形的面积 与四边形的面积 之比为4∶5,若 ,则此三角形移动的距离 是.
13. 如图,把 沿 边平移到 的位置,图中所示的三角形的面积 与四边形的面积 之比为4∶5,若 ,则此三角形移动的距离 是. 14. 如图,在 中, , .将 绕点B逆时针旋转60°,得到 ,则 边的中点D与其对应点 的距离是.
14. 如图,在 中, , .将 绕点B逆时针旋转60°,得到 ,则 边的中点D与其对应点 的距离是.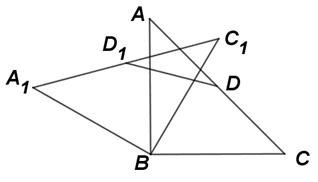 15. 如图,为了了解山坡上两棵树间的水平距离,数学活动小组的同学们测得该山坡的倾斜角 ,两树间的坡面距离 ,则这两棵树的水平距离约为m(结果精确到 ,参考数据: ).
15. 如图,为了了解山坡上两棵树间的水平距离,数学活动小组的同学们测得该山坡的倾斜角 ,两树间的坡面距离 ,则这两棵树的水平距离约为m(结果精确到 ,参考数据: ).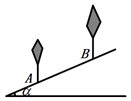 16. 甲、乙两人沿笔直公路匀速由A地到B地,甲先出发30分钟,到达B地后原路原速返回与乙在C地相遇.甲的速度比乙的速度快 ,甲、乙两人与A地的距离 和乙行驶的时间 之间的函数关系如图所示,则B,C两地的距离为 (结果精确到 ).
16. 甲、乙两人沿笔直公路匀速由A地到B地,甲先出发30分钟,到达B地后原路原速返回与乙在C地相遇.甲的速度比乙的速度快 ,甲、乙两人与A地的距离 和乙行驶的时间 之间的函数关系如图所示,则B,C两地的距离为 (结果精确到 ).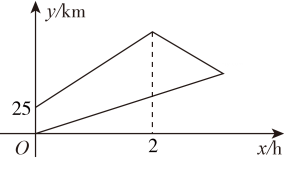
三、解答题
-
17. 先化简,再求值: ,其中 .18. 如图, 在平面直角坐标系中,顶点的坐标分别为 , , .
 (1)、画出与 关于y轴对称的 ;(2)、将 绕点 顺时针旋转90°得到 , 弧是点A所经过的路径,则旋转中心 的坐标为.(3)、求图中阴影部分的面积(结果保留 ).19. 在“尚科学,爱运动”主题活动中,某校在七年级学生中随机抽取部分同学就“一分钟跳绳”进行测试,并将测试成绩x(单位:次)进行整理后分成六个等级,分别用A,B,C,D,E,F表示,并绘制成如图所示的两幅不完整的统计图表.请根据图表中所给出的信息解答下列问题:
(1)、画出与 关于y轴对称的 ;(2)、将 绕点 顺时针旋转90°得到 , 弧是点A所经过的路径,则旋转中心 的坐标为.(3)、求图中阴影部分的面积(结果保留 ).19. 在“尚科学,爱运动”主题活动中,某校在七年级学生中随机抽取部分同学就“一分钟跳绳”进行测试,并将测试成绩x(单位:次)进行整理后分成六个等级,分别用A,B,C,D,E,F表示,并绘制成如图所示的两幅不完整的统计图表.请根据图表中所给出的信息解答下列问题:组别
成绩x(单位:次)
人数
A
4
B
15
C
18
D
12
E
m
F
5
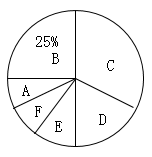 (1)、本次测试随机抽取的人数是人, ;(2)、求C等级所在扇形的圆心角的度数;(3)、若该校七年级学生共有300人,且规定不低于130次的成绩为优秀,请你估计该校七年级学生中有多少人能够达到优秀.20. 在抗击新冠肺炎疫情期间,玉龙社区购买酒精和消毒液两种消毒物资,供居民使用.第一次购买酒精和消毒液若干,酒精每瓶10元,消毒液每瓶5元,共花费了350元;第二次又购买了与第一次相同数量的酒精和消毒液,由于酒精和消毒液每瓶价格分别下降了30%和20%,只花费了260元.(1)、求每次购买的酒精和消毒液分别是多少瓶?(2)、若按照第二次购买的价格再一次购买,根据需要,购买的酒精数量是消毒液数量的2倍,现有购买资金200元,则最多能购买消毒液多少瓶?21. 如图,正方形 和正方形 (其中 ), 的延长线与直线 交于点H.
(1)、本次测试随机抽取的人数是人, ;(2)、求C等级所在扇形的圆心角的度数;(3)、若该校七年级学生共有300人,且规定不低于130次的成绩为优秀,请你估计该校七年级学生中有多少人能够达到优秀.20. 在抗击新冠肺炎疫情期间,玉龙社区购买酒精和消毒液两种消毒物资,供居民使用.第一次购买酒精和消毒液若干,酒精每瓶10元,消毒液每瓶5元,共花费了350元;第二次又购买了与第一次相同数量的酒精和消毒液,由于酒精和消毒液每瓶价格分别下降了30%和20%,只花费了260元.(1)、求每次购买的酒精和消毒液分别是多少瓶?(2)、若按照第二次购买的价格再一次购买,根据需要,购买的酒精数量是消毒液数量的2倍,现有购买资金200元,则最多能购买消毒液多少瓶?21. 如图,正方形 和正方形 (其中 ), 的延长线与直线 交于点H.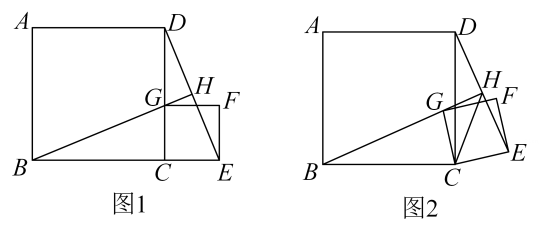 (1)、如图1,当点G在 上时,求证: , ;(2)、将正方形 绕点C旋转一周.
(1)、如图1,当点G在 上时,求证: , ;(2)、将正方形 绕点C旋转一周.①如图2,当点E在直线 右侧时,求证: ;
②当 时,若 , ,请直接写出线段 的长
22. 如图,二次函数 的图象交x轴于点 , ,交y轴于点C.点 是x轴上的一动点, 轴,交直线 于点M,交抛物线于点N. (1)、求这个二次函数的表达式;(2)、①若点P仅在线段 上运动,如图1.求线段 的最大值;
(1)、求这个二次函数的表达式;(2)、①若点P仅在线段 上运动,如图1.求线段 的最大值;②若点P在x轴上运动,则在y轴上是否存在点Q,使以M,N,C,Q为顶点的四边形为菱形.若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.