江苏省镇江市2020年中考数学试卷
试卷更新日期:2020-08-24 类型:中考真卷
一、选择题
-
1. 下列计算正确的是( )A、a3+a3=a6 B、(a3)2=a6 C、a6÷a2=a3 D、(ab)3=ab32. 如图,将棱长为6的正方体截去一个棱长为3的正方体后,得到一个新的几何体,这个几何体的主视图是( )
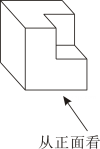 A、
A、 B、
B、 C、
C、 D、
D、 3. 一次函数y=kx+3(k≠0)的函数值y随x的增大而增大,它的图象不经过的象限是( )A、第一 B、第二 C、第三 D、第四4. 如图,AB是半圆的直径,C、D是半圆上的两点,∠ADC=106°,则∠CAB等于( )
3. 一次函数y=kx+3(k≠0)的函数值y随x的增大而增大,它的图象不经过的象限是( )A、第一 B、第二 C、第三 D、第四4. 如图,AB是半圆的直径,C、D是半圆上的两点,∠ADC=106°,则∠CAB等于( )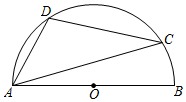 A、10° B、14° C、16° D、26°5. 点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上.则m﹣n的最大值等于( )A、 B、4 C、﹣ D、﹣6. 如图①,AB=5,射线AM∥BN,点C在射线BN上,将△ABC沿AC所在直线翻折,点B的对应点D落在射线BN上,点P,Q分别在射线AM、BN上,PQ∥AB.设AP=x,QD=y.若y关于x的函数图象(如图②)经过点E(9,2),则cosB的值等于( )
A、10° B、14° C、16° D、26°5. 点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上.则m﹣n的最大值等于( )A、 B、4 C、﹣ D、﹣6. 如图①,AB=5,射线AM∥BN,点C在射线BN上,将△ABC沿AC所在直线翻折,点B的对应点D落在射线BN上,点P,Q分别在射线AM、BN上,PQ∥AB.设AP=x,QD=y.若y关于x的函数图象(如图②)经过点E(9,2),则cosB的值等于( )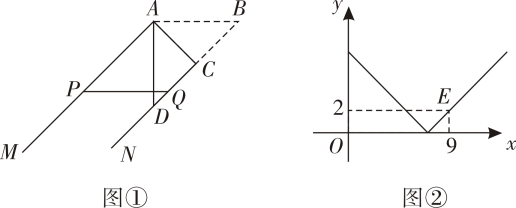 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
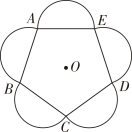
7. 倒数是.8. 使 有意义的x的取值范围是 .9. 分解因式:9x2-1= .10. 2020年我国将完成脱贫攻坚目标任务.从2012年底到2019年底,我国贫困人口减少了93480000人,用科学记数法把93480000表示为.11. 一元二次方程x2﹣2x=0的解是 .12. 一只不透明的袋子中装有5个红球和1个黄球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸出红球的概率等于.13. 圆锥底面圆半径为5,母线长为6,则圆锥侧面积等于.14. 点O是正五边形ABCDE的中心,分别以各边为直径向正五边形的外部作半圆,组成了一幅美丽的图案(如图).这个图案绕点O至少旋转°后能与原来的图案互相重合.
 15. 根据数值转换机的示意图,输出的值为.
15. 根据数值转换机的示意图,输出的值为. 16. 如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为°.
16. 如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为°.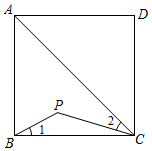 17. 在从小到大排列的五个数x,3,6,8,12中再加入一个数,若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等,则x的值为.18. 如图,在△ABC中,BC=3,将△ABC平移5个单位长度得到△A1B1C1 , 点P、Q分别是AB、A1C1的中点,PQ的最小值等于.
17. 在从小到大排列的五个数x,3,6,8,12中再加入一个数,若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等,则x的值为.18. 如图,在△ABC中,BC=3,将△ABC平移5个单位长度得到△A1B1C1 , 点P、Q分别是AB、A1C1的中点,PQ的最小值等于.
三、解答题
-
19.(1)、计算:4sin60°﹣ +( ﹣1)0;(2)、化简(x+1)÷(1+ ).20.(1)、解方程: = +1;(2)、解不等式组:21. 如图,AC是四边形ABCD的对角线,∠1=∠B,点E、F分别在AB、BC上,BE=CD,BF=CA,连接EF.
 (1)、求证:∠D=∠2;(2)、若EF∥AC,∠D=78°,求∠BAC的度数.22. 教育部发布的义务教育质量监测结果报告显示,我国八年级学生平均每天的睡眠时间达9小时及以上的比例为19.4%.某校数学社团成员采用简单随机抽样的方法,抽取了本校八年级50名学生,对他们一周内平均每天的睡眠时间t(单位:小时)进行了调查,将数据整理后绘制成下表:
(1)、求证:∠D=∠2;(2)、若EF∥AC,∠D=78°,求∠BAC的度数.22. 教育部发布的义务教育质量监测结果报告显示,我国八年级学生平均每天的睡眠时间达9小时及以上的比例为19.4%.某校数学社团成员采用简单随机抽样的方法,抽取了本校八年级50名学生,对他们一周内平均每天的睡眠时间t(单位:小时)进行了调查,将数据整理后绘制成下表:平均每天的睡眠时间分组
5≤t<6
6≤t<7
7≤t<8
8≤t<9
9小时及以上
频数
1
5
m
24
n
该样本中学生平均每天的睡眠时间达9小时及以上的比例高于全国的这项数据,达到了22%.
(1)、求表格中n的值;(2)、该校八年级共400名学生,估计其中平均每天的睡眠时间在7≤t<8这个范围内的人数是多少.23. 智慧的中国古代先民发明了抽象的符号来表达丰富的含义.例如,符号“ ”有刚毅的含义,符号“
”有刚毅的含义,符号“  ”有愉快的含义.符号中的“
”有愉快的含义.符号中的“  ”表示“阴”,“
”表示“阴”,“  ”表示“阳”,类似这样自上而下排成的三行符号还有其他的含义.所有这些三行符号中,每一行只有一个阴或一个阳,且出现阴、阳的可能性相同. (1)、所有这些三行符号共有种;(2)、若随机画一个这样的三行符号,求“画出含有一个阴和两个阳的三行符号”的概率.24. 如图,点E与树AB的根部点A、建筑物CD的底部点C在一条直线上,AC=10m.小明站在点E处观测树顶B的仰角为30°,他从点E出发沿EC方向前进6m到点G时,观测树顶B的仰角为45°,此时恰好看不到建筑物CD的顶部D(H、B、D三点在一条直线上).已知小明的眼睛离地面1.6m,求建筑物CD的高度(结果精确到0.1m).(参考数据: ≈1.41, ≈1.73.)
”表示“阳”,类似这样自上而下排成的三行符号还有其他的含义.所有这些三行符号中,每一行只有一个阴或一个阳,且出现阴、阳的可能性相同. (1)、所有这些三行符号共有种;(2)、若随机画一个这样的三行符号,求“画出含有一个阴和两个阳的三行符号”的概率.24. 如图,点E与树AB的根部点A、建筑物CD的底部点C在一条直线上,AC=10m.小明站在点E处观测树顶B的仰角为30°,他从点E出发沿EC方向前进6m到点G时,观测树顶B的仰角为45°,此时恰好看不到建筑物CD的顶部D(H、B、D三点在一条直线上).已知小明的眼睛离地面1.6m,求建筑物CD的高度(结果精确到0.1m).(参考数据: ≈1.41, ≈1.73.)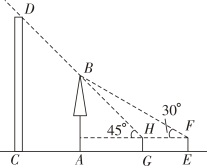 25. 如图,正比例函数y=kx(k≠0)的图象与反比例函数y=﹣ 的图象交于点A(n,2)和点B.
25. 如图,正比例函数y=kx(k≠0)的图象与反比例函数y=﹣ 的图象交于点A(n,2)和点B.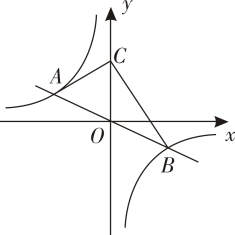 (1)、n= , k=;(2)、点C在y轴正半轴上.∠ACB=90°,求点C的坐标;(3)、点P(m,0)在x轴上,∠APB为锐角,直接写出m的取值范围.26. 如图,▱ABCD中,∠ABC的平分线BO交边AD于点O,OD=4,以点O为圆心,OD长为半径作⊙O,分别交边DA、DC于点M、N.点E在边BC上,OE交⊙O于点G,G为 的中点.
(1)、n= , k=;(2)、点C在y轴正半轴上.∠ACB=90°,求点C的坐标;(3)、点P(m,0)在x轴上,∠APB为锐角,直接写出m的取值范围.26. 如图,▱ABCD中,∠ABC的平分线BO交边AD于点O,OD=4,以点O为圆心,OD长为半径作⊙O,分别交边DA、DC于点M、N.点E在边BC上,OE交⊙O于点G,G为 的中点. (1)、求证:四边形ABEO为菱形;(2)、已知cos∠ABC= ,连接AE,当AE与⊙O相切时,求AB的长.27.(1)、(算一算)
(1)、求证:四边形ABEO为菱形;(2)、已知cos∠ABC= ,连接AE,当AE与⊙O相切时,求AB的长.27.(1)、(算一算)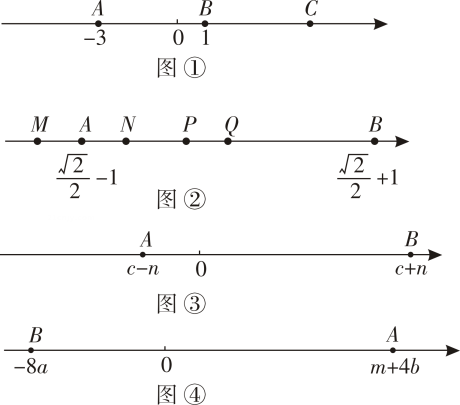
如图①,点A、B、C在数轴上,B为AC的中点,点A表示﹣3,点B表示1,则点C表示的数为 , AC长等于;
(2)、(找一找)如图②,点M、N、P、Q中的一点是数轴的原点,点A、B分别表示实数 ﹣1、 +1,Q是AB的中点,则点是这个数轴的原点;
(3)、(画一画)如图③,点A、B分别表示实数c﹣n、c+n,在这个数轴上作出表示实数n的点E(要求:尺规作图,不写作法,保留作图痕迹);
(4)、(用一用)学校设置了若干个测温通道,学生进校都应测量体温,已知每个测温通道每分钟可检测a个学生.凌老师提出了这样的问题:假设现在校门口有m个学生,每分钟又有b个学生到达校门口.如果开放3个通道,那么用4分钟可使校门口的学生全部进校;如果开放4个通道,那么用2分钟可使校门口的学生全部进校.在这些条件下,a、m、b会有怎样的数量关系呢?
爱思考的小华想到了数轴,如图④,他将4分钟内需要进校的人数m+4b记作+(m+4b),用点A表示;将2分钟内由4个开放通道检测后进校的人数,即校门口减少的人数8a记作﹣8a,用点B表示.
①用圆规在小华画的数轴上分别画出表示+(m+2b)、﹣12a的点F、G,并写出+(m+2b)的实际意义;
②写出a、m的数量关系.
28. 如图①,直线l经过点(4,0)且平行于y轴,二次函数y=ax2﹣2ax+c(a、c是常数,a<0)的图象经过点M(﹣1,1),交直线l于点N,图象的顶点为D,它的对称轴与x轴交于点C,直线DM、DN分别与x轴相交于A、B两点. (1)、当a=﹣1时,求点N的坐标及 的值;(2)、随着a的变化, 的值是否发生变化?请说明理由;(3)、如图②,E是x轴上位于点B右侧的点,BC=2BE,DE交抛物线于点F.若FB=FE,求此时的二次函数表达式.
(1)、当a=﹣1时,求点N的坐标及 的值;(2)、随着a的变化, 的值是否发生变化?请说明理由;(3)、如图②,E是x轴上位于点B右侧的点,BC=2BE,DE交抛物线于点F.若FB=FE,求此时的二次函数表达式.