陕西省榆林市定边县2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-08-24 类型:期末考试
一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题目要求的)
-
1. 使分式 有意义,x的取值是( )A、x≠﹣2 B、x≠2 C、x≠±2 D、x≠12. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
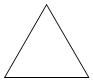 B、
B、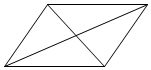 C、
C、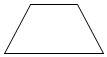 D、
D、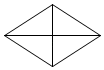 3. 如果a<b,那么下列结论不正确的是( )A、a+3<b+3 B、a﹣3<b﹣3 C、3a<3b D、﹣3a<﹣3b4. 下列从左到右的变形属于因式分解的是( )A、a(x+y)=ax+ay B、x2+2x+1=x(x+2)+1 C、x2﹣1=(x+1)(x﹣1) D、(x+2)(x﹣2)=x2﹣45. 若n边形的内角和等于外角和的3倍,则边数n为( )A、6 B、7 C、8 D、96. 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿BC方向平移2个单位后得到△DEF,连接DC,则DC的长为( )
3. 如果a<b,那么下列结论不正确的是( )A、a+3<b+3 B、a﹣3<b﹣3 C、3a<3b D、﹣3a<﹣3b4. 下列从左到右的变形属于因式分解的是( )A、a(x+y)=ax+ay B、x2+2x+1=x(x+2)+1 C、x2﹣1=(x+1)(x﹣1) D、(x+2)(x﹣2)=x2﹣45. 若n边形的内角和等于外角和的3倍,则边数n为( )A、6 B、7 C、8 D、96. 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿BC方向平移2个单位后得到△DEF,连接DC,则DC的长为( )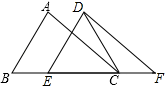 A、3 B、4 C、5 D、67. 如图,已知直线y1=ax+b与y2=mx+n相交于点A(2,﹣1),若y1>y2 , 则x的取值范围是( )
A、3 B、4 C、5 D、67. 如图,已知直线y1=ax+b与y2=mx+n相交于点A(2,﹣1),若y1>y2 , 则x的取值范围是( )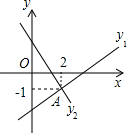 A、x<2 B、x>2 C、x<﹣1 D、x>﹣18. 如图,在▱ABCD中,DE平分∠ADC,AD=8,BE=3,则▱ABCD的周长是( )
A、x<2 B、x>2 C、x<﹣1 D、x>﹣18. 如图,在▱ABCD中,DE平分∠ADC,AD=8,BE=3,则▱ABCD的周长是( )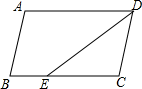 A、16 B、14 C、26 D、249. 小明要从甲地到乙地,两地相距1.8千米.已知他步行的平均速度为90米/分,跑步的平均速度为210米/分,若他要在不超过15分钟的时间内从甲地到达乙地,至少需要跑步多少分钟?设他需要跑步x分钟,则列出的不等式为( )A、210x+90(15﹣x)≥1800 B、90x+210(15﹣x)≤1800 C、210x+90(15﹣x)≥1.8 D、90x+210(15﹣x)≤1.810. 如图,在△ABE中,AE的垂直平分线MN交BE于点C,∠E=30°,且AB=CE,则∠BAE的度数是( )
A、16 B、14 C、26 D、249. 小明要从甲地到乙地,两地相距1.8千米.已知他步行的平均速度为90米/分,跑步的平均速度为210米/分,若他要在不超过15分钟的时间内从甲地到达乙地,至少需要跑步多少分钟?设他需要跑步x分钟,则列出的不等式为( )A、210x+90(15﹣x)≥1800 B、90x+210(15﹣x)≤1800 C、210x+90(15﹣x)≥1.8 D、90x+210(15﹣x)≤1.810. 如图,在△ABE中,AE的垂直平分线MN交BE于点C,∠E=30°,且AB=CE,则∠BAE的度数是( ) A、80° B、85° C、90° D、105°
A、80° B、85° C、90° D、105°二、填空题(共4小题,每小题3分,计12分)
-
11. 因式分解:2a2﹣4a=.12. 若解分式方程 有增根,则k=.13. 如图,在▱ABCD中,AB=4,BC=9,∠B=30°,则▱ABCD的面积是.
 14. 如图所示,在四边形ABCD中,AB=CD=4,M、N、P分别是AD、BC、BD的中点,∠ABD=20°,∠BDC=80°,则MN的长是.
14. 如图所示,在四边形ABCD中,AB=CD=4,M、N、P分别是AD、BC、BD的中点,∠ABD=20°,∠BDC=80°,则MN的长是.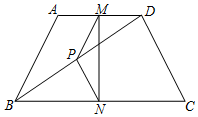
三、解答题(共11小题,计78分.解答应写出过程)
-
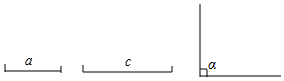
15. 解分式方程: .16. 解不等式组:17. 先化简,再求值: ,其中a=3.18. 如图,已知线段a,c(a<c),直角α,用尺规作图法求作Rt△ABC,使∠C=∠α,BC=a,AB=c.(保留作图痕迹,不写作法)
 19. 如图,在四边形ABCD中,∠B=∠D,∠1=∠2,求证:四边形ABCD是平行四边形.
19. 如图,在四边形ABCD中,∠B=∠D,∠1=∠2,求证:四边形ABCD是平行四边形.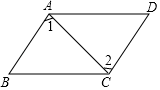 20. 已知:如图,在△ABC中,AB=AC,点D,E分别在边AC,AB上,且∠ABD=∠ACE.BD与CE相交于点O.
20. 已知:如图,在△ABC中,AB=AC,点D,E分别在边AC,AB上,且∠ABD=∠ACE.BD与CE相交于点O.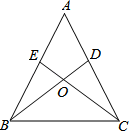
求证:
(1)、OB=OC;(2)、BE=CD.21. 如图,小红想测量离A处30m的大树的高度,她站在A处仰望树顶B,仰角为30°(即∠BDE=30°),已知小红身高1.52m.求大树的高度.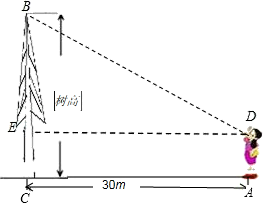 22. 在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
22. 在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
( 1 )将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
( 2 )将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2 , 并直接写出点B2、C2的坐标.
23. 某单位要制作一批宣传材料,甲公司提出:每份材料收费20元,另收3000元设计费;乙公司提出:每份材料收费30元,不收设计费.(1)、什么情况下选择甲公司比较合算?(2)、什么情况下选择乙公司比较合算?(3)、什么情况下两公司的费用相同?24. 新冠肺炎疫情防控期间,学校为做好预防消毒工作,开学初购进A,B两种消毒液,购买A种消毒液花费了2500元,购买B种消毒液花费了2000元,且购买A种消毒液数量是购买B种消毒液数量的2倍,已知购买一桶B种消毒液比购买一桶A种消毒液多花30元.(1)、求购买一桶A种、一桶B种消毒液各需多少元?(2)、为了践行“把人民群众生命安全和身体健康摆在第一位”的要求,加强学校防控工作,保障师生健康安全,学校准备再次购买一批防控物资.其中A,B两种消毒液准备购买共50桶.如果学校此次购买A、B两种消毒液的总费用不超过3250元,那么学校此次最多可购买多少桶B种消毒液?25. 如图,四边形ABCD中,∠ABC=∠ADC=45°,将△BCD绕点C顺时针旋转一定角度后,点B的对应点恰好与点A重合,得到△ACE.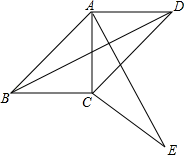 (1)、请求出旋转角的度数;(2)、请判断AE与BD的位置关系,并说明理由;(3)、若AD=2,CD=3,试求出四边形ABCD的对角线BD的长.
(1)、请求出旋转角的度数;(2)、请判断AE与BD的位置关系,并说明理由;(3)、若AD=2,CD=3,试求出四边形ABCD的对角线BD的长.