浙江省宁波市北仑区2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2020-08-24 类型：期末考试

进入出卷网下载

一、单选题

1. 世界上最小、最轻的昆虫是膜翅目缨小蜂科的一种卵蜂，其质量仅有0.000005克，用科学记数法表示0.000005，正确的是（）

A、 $5 \times 10^{- 6}$ B、 $5 \times 10^{- 5}$ C、 $5 \times 10^{6}$ D、 $5 \times 10^{5}$

查看试题解析
2. 下列运算中，正确的是（）

A、（3cd）³＝9c³d³ B、（﹣3a³）²＝﹣9a⁵ C、{（﹣a）³}⁴＝﹣a¹² D、（﹣a）•（a²）³＝﹣a⁷

查看试题解析
3. 下列多项式能用公式法分解因式的是（）

A、 $4 x^{2} + {(- y)}^{2}$ B、 $- 4 x^{2} - y^{2}$ C、 $x^{2} + 2 x y - y^{2}$ D、 $x + 1 + \frac{x^{2}}{4}$

查看试题解析
4. 若分式 $\frac{a^{2} - 16}{a^{2} - 4 a}$ 的值为0，则a的值为（）

A、4和﹣4 B、4 C、﹣4 D、4和0

查看试题解析
5. 若 $(x - 1) (x + 3) = x^{2} + m x + n$ ，那么 $m, n$ 的值分别是（）

A、m=1，n=3 B、m=4，n=5 C、m=2，n=-3 D、m=-2 ，n=3

查看试题解析
6. 我国古代数学名著《孙子算经》中记载了一道题，大意是：100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，问有多少匹大马、多少匹小马？若设大马有x匹，小马有y匹，那么可列方程组为（）

A、 ${\begin{array}{l} x + y = 100 \\ 3 x + 3 y = 100 \end{array}$ B、 ${\begin{array}{l} x + y = 100 \\ x + \frac{1}{3} y = 100 \end{array}$ C、 ${\begin{array}{l} x + y = 100 \\ 3 x + \frac{1}{3} y = 100 \end{array}$ D、 ${\begin{array}{l} x + y = 100 \\ 3 x + y = 100 \end{array}$

查看试题解析
7.
如图，下列说法错误的是（　　）

A、∠A与∠EDC是同位角 B、∠A与∠ABF是内错角 C、∠A与∠ADC是同旁内角 D、∠A与∠C是同旁内角

查看试题解析
8. 当a为何值时，方程组 ${\begin{array}{l} 3 x - 5 y = 2 a \\ 2 x + 7 y = a - 18 \end{array}$ 的解，x、y的值互为相反数（）

A、a＝﹣8 B、a＝8 C、a＝10 D、a＝﹣10

查看试题解析
9. 把一张对边互相平行的纸条按如图所示折叠，EF是折痕，若∠EFB＝34°，则下列结论不正确的是（）

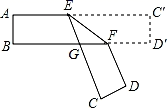A、 $∠ C^{'} E F ＝ 34 °$ B、∠AEC＝146° C、∠BGE＝68° D、∠BFD＝112°

查看试题解析
10. 任何一个正整数n都可以进行这样的分解：n＝s×t（s，t是正整数，且s≤t），如果p×q在n的所有分解中两因数之差的绝对值最小，我们就称p×q是n的最优分解，并规定：F（n）＝ $\frac{p}{q}$ .例如24可以分解成1×24，2×12，3×8，4×6这四种，这时就有F（24）＝ $\frac{4}{6}$ ＝ $\frac{2}{3}$ .给出下列关于F（n）的说法：①F（6）＝ $\frac{2}{3}$ ；②F（16）＝1；③F（n²﹣n）＝1﹣ $\frac{1}{n}$ ；④若n是一个完全平方数，F（n）＝1.其中说法正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. （﹣2）⁰×（ $\frac{1}{2}$ ）^﹣¹＝.

查看试题解析
12. 如图所示，直线a∥b，如果∠1＝45°，那么∠2的度数是.

查看试题解析
13. 已知3x﹣2y﹣3＝0，求2^3x÷2^2y＝.

查看试题解析
14. 若分式方程 $\frac{a}{x + 2}$ ＝4﹣ $\frac{2}{x + 2}$ 无解，则a的值为.

查看试题解析
15. 多项式 $\frac{1}{4} x^{2} + m x + 1$ 是完全平方式，则m＝.

查看试题解析
16. 若方程组 ${\begin{array}{l} 3 x + 4 y = 12.5 \\ 2 x + 5 y = 13 \end{array}$ 的解是 ${\begin{array}{l} x = 1.5 \\ y = 2 \end{array}$ ，请求出方程组 ${\begin{array}{l} 3 (m - 5) + 4 (n + 3) = 12.5 \\ 2 (m - 5) + 5 (n + 3) = 13 \end{array}$ 中m，n的值，m＝， n＝.

查看试题解析
17. 若|a﹣1|+（ab﹣2）²＝0，则 $\frac{1}{a b} + \frac{1}{(a + 1) (b + 1)}$ $+$ … $+$ $\frac{1}{(a + 10) (b + 10)}$ ＝.

查看试题解析
18. 如图，把四张大小相同的长方形卡片（如图①）按图2、图③两种方式放在一个底面为长方形（长比宽多5cm）的盒底上，底面未被卡片覆盖的部分用阴影表示，若记图②中阴影部分的周长为C₁ ，图3中阴影部分的周长为C₂ ，那么C₁比C₂大cm.

查看试题解析

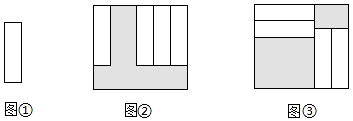
三、解答题

19.

(1)、计算：（3x²）³•（﹣2x⁴）÷（﹣9x⁷）；

(2)、因式分解：﹣2m³+24m²﹣72m.

查看试题解析
20. 先化简 $(1 - \frac{1}{x - 1}) \div \frac{x^{2} - 4 x + 4}{x^{2} - 1}$ ，然后从－2≤x≤2的范围内选取一个合适的整数作为x的值代入求值.

查看试题解析
21. 解方程或方程组：

(1)、 ${\begin{array}{l} 4 (x - y - 1) = 3 (1 - y) - 2 \\ \frac{x}{2} + \frac{y}{3} = 2 \end{array}$ ；

(2)、 $\frac{3}{x - 1} + \frac{4 x}{1 - x^{2}}$ ＝ $\frac{1}{x + 1}$ .

查看试题解析
22. 某社区积极响应正在开展的“文明城市创建工作”，组织甲、乙两个志愿工程队对社区的一些区域进行绿化改造.已知甲工程队每小时能完成的绿化面积是乙工程队每小时能完成的绿化面积的2倍，并且甲工程队完成300m²的绿化面积比乙工程队完成200m²的绿化面积少用2h.求乙工程队每小时能完成多少平方米的绿化面积？

查看试题解析
23. 对于二次三项式a²+6a+9，可以用公式法将它分解成（a+3）²的形式，但对于二次三项式a²+6a+8，就不能直接应用完全平方式了，我们可以在二次三项式中先加上一项9，使其成为完全平方式，再减去9这项，使整个式子的值保持不变，于是有：a²+6a+8＝a²+6a+9﹣9+8＝（a+3）²﹣1＝[（a+3）+1][（a+3）﹣1]＝（a+4）（a+2），请仿照上面的做法，将下列各式因式分解：

(1)、x²﹣6x﹣16；

(2)、x²+2ax﹣3a².

查看试题解析
24. 两个边长分别为a和b的正方形如图放置（图1），其未叠合部分（阴影）面积为S₁；若再在图1中大正方形的右下角摆放一个边长为b的小正方形（如图2），两个小正方形叠合部分（阴影）面积为S₂.

(1)、用含a，b的代数式分别表示S₁、S₂；

(2)、若a+b＝10，ab＝20，求S₁+S₂的值；

(3)、当S₁+S₂＝30时，求出图3中阴影部分的面积S₃.

查看试题解析
25. 阅读下列材料，然后解答后面的问题.
我们知道方程2x+3y＝12有无数组解，但在实际生活中我们往往只需求出其正整数解.

例：由2x+3y＝12得y＝ $\frac{12 - 2 x}{3}$ ＝4﹣ $\frac{2}{3}$ x（x，y为正整数）.

∴ ${\begin{array}{l} x > 0 \\ 12 - 2 x > 0 \end{array}$ 则有0＜x＜6，

又∵y＝4﹣ $\frac{2}{3}$ x为正整数，

∴ $\frac{2}{3}$ x为正整数.

由2与3互质，可知x为3的倍数，从而x＝3，代入y＝4﹣ $\frac{2}{3}$ x＝2.

∴2x+3y＝12的正整数解为 ${\begin{array}{l} x = 3 \\ y = 2 \end{array}$ .

问题：

(1)、请你写出方程3x+y＝7的一组正整数解：.

(2)、若 $\frac{9}{x - 2}$ 为自然数，则满足条件的x值有 .

A、2个 B、3个 C、4个 D、5个

(3)、为了开展“阳光体育”活动，某班计划购买甲、乙两种体育用品（每种体育用品至少购买1件），其中甲种体育用品每件20元，乙种体育用品每件30元，共用去180元，问有几种购买方案.

查看试题解析
26. “一带一路”让中国和世界更紧密，“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示，灯A射线从AM开始顺时针旋转至AN便立即回转，灯B射线从BP开始顺时针旋转至BQ便立即回转，两灯不停交叉照射巡视.若灯A转动的速度是每秒2度，灯B转动的速度是每秒1度.假定主道路是平行的，即PQ∥MN，且∠BAM：∠BAN=2：1.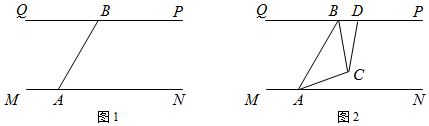

(1)、填空：∠BAN=°；

(2)、若灯B射线先转动30秒，灯A射线才开始转动，在灯B射线到达BQ之前，A灯转动几秒，两灯的光束互相平行？

(3)、如图2，若两灯同时转动，在灯A射线到达AN之前.若射出的光束交于点C，过C作∠ACD交PQ于点D，且∠ACD=120°，则在转动过程中，请探究∠BAC与∠BCD的数量关系是否发生变化？若不变，请求出其数量关系；若改变，请说明理由.

查看试题解析