浙江省温州市2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-08-24 类型:期末考试
一、单选题
-
1. 下列四个交通标志中,是中心对称图形的标志是( )A、
 B、
B、 C、
C、 D、
D、 2. 二次根式 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、3. 校田径队有9名同学,他们的100米跑步成绩各不相同,现要从中选4名参加运动会 米接力项目.若他们只知道自己的成绩,要判断自己是否入选,教练只需公布他们成绩的( )A、平均数 B、中位数 C、众数 D、方差4. 如图,四边形 是平行四边形, 是 延长线上的一点,若 ,则 的度数是( )
2. 二次根式 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、3. 校田径队有9名同学,他们的100米跑步成绩各不相同,现要从中选4名参加运动会 米接力项目.若他们只知道自己的成绩,要判断自己是否入选,教练只需公布他们成绩的( )A、平均数 B、中位数 C、众数 D、方差4. 如图,四边形 是平行四边形, 是 延长线上的一点,若 ,则 的度数是( )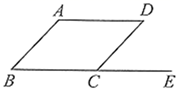 A、 B、 C、 D、5. 如图,商用手扶梯 的坡比为 ,已知扶梯的长 为12米,则小明乘坐扶梯从 处到 处上升的高度 为( )
A、 B、 C、 D、5. 如图,商用手扶梯 的坡比为 ,已知扶梯的长 为12米,则小明乘坐扶梯从 处到 处上升的高度 为( ) A、6米 B、 米 C、12米 D、 米6. 已知A(x1 , y1)、B(x2 , y2)均在反比例函数y= 的图象上,若0<x1<x2 , 则y1、y2的大小关系为( )A、y1<y2<0 B、y2<y1<0 C、0<y1<y2 D、0<y2<y17. 用反证法证明“在同一平面内,若 , ,则 ”时,应假设( )A、 B、 C、 , D、 与 相交8. 如图,在 中,点 , , 分别是边 , , 的中点,若 ,则四边形 的周长为( )
A、6米 B、 米 C、12米 D、 米6. 已知A(x1 , y1)、B(x2 , y2)均在反比例函数y= 的图象上,若0<x1<x2 , 则y1、y2的大小关系为( )A、y1<y2<0 B、y2<y1<0 C、0<y1<y2 D、0<y2<y17. 用反证法证明“在同一平面内,若 , ,则 ”时,应假设( )A、 B、 C、 , D、 与 相交8. 如图,在 中,点 , , 分别是边 , , 的中点,若 ,则四边形 的周长为( ) A、1 B、2 C、4 D、89. 如图,在一块长为 ,宽为 的矩形 空地内修建四条宽度相等,且与矩形各边垂直的道路.四条道路围成的中间部分恰好是一个正方形,且边长是道路宽的4倍,道路占地总面积为 .设道路宽为 ,则以下方程正确的是( )
A、1 B、2 C、4 D、89. 如图,在一块长为 ,宽为 的矩形 空地内修建四条宽度相等,且与矩形各边垂直的道路.四条道路围成的中间部分恰好是一个正方形,且边长是道路宽的4倍,道路占地总面积为 .设道路宽为 ,则以下方程正确的是( )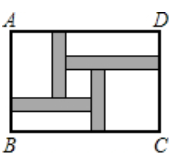 A、 B、 C、 D、10. 如图,已知点 是线段 的中点, 且 .延长 至点 ,使得 .以 , 为边作矩形 .连结并延长 ,交 的延长线于点 ,连结 , .《几何原本》中利用该图解释了代数式 的几何意义.则 的值为( )
A、 B、 C、 D、10. 如图,已知点 是线段 的中点, 且 .延长 至点 ,使得 .以 , 为边作矩形 .连结并延长 ,交 的延长线于点 ,连结 , .《几何原本》中利用该图解释了代数式 的几何意义.则 的值为( )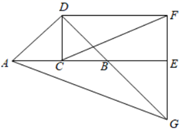 A、 B、2 C、 D、
A、 B、2 C、 D、二、填空题
-
11. 化简二次根式 的结果是.12. 甲、乙两位同学进行打字比赛,各自录入同一篇800字的文章,两人在比赛开始后前五分钟打字速度(单位:个/分钟)的折线统计图如图,则每分钟打字速度更稳定的是(填“甲”或“乙”)同学.
 13. 如果一个多边形的内角和是1800°,那么这个多边形的边数是 .14. 若关于x的一元二次方程 有两个相等的实数根,则c的值是.15. 如图,菱形 的对角线 , 相交于点 ,已知 ,菱形 的面积为24,则 的长为.
13. 如果一个多边形的内角和是1800°,那么这个多边形的边数是 .14. 若关于x的一元二次方程 有两个相等的实数根,则c的值是.15. 如图,菱形 的对角线 , 相交于点 ,已知 ,菱形 的面积为24,则 的长为. 16. 若关于 的一元二次方程 的解为 , ,则关于 的一元二次方程 的解为.17. 如图, , , 是反比例函数 在第一象限的图象上的点,它们的横坐标分别为2,4,6.过点 , , 分别作 轴, 轴的垂线段,构成多个矩形.若图中阴影部分的面积为12,则点 的坐标为.
16. 若关于 的一元二次方程 的解为 , ,则关于 的一元二次方程 的解为.17. 如图, , , 是反比例函数 在第一象限的图象上的点,它们的横坐标分别为2,4,6.过点 , , 分别作 轴, 轴的垂线段,构成多个矩形.若图中阴影部分的面积为12,则点 的坐标为.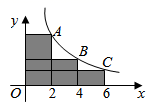 18. 图1是上下都安装“摩擦铰链”的平开窗,滑轨 固定在窗框,托悬臂 安装在窗扇. , , 分别是 , , 上固定的点,且 .当窗户开到最大时, ,且点 到 的距离为 ,此时主轴 与 的夹角 .如图2,窗户从开到最大到关闭( , , , 与 重合)的过程中,控制臂 , 带动 上的滑块 向点 滑动了 .则 的长为 .
18. 图1是上下都安装“摩擦铰链”的平开窗,滑轨 固定在窗框,托悬臂 安装在窗扇. , , 分别是 , , 上固定的点,且 .当窗户开到最大时, ,且点 到 的距离为 ,此时主轴 与 的夹角 .如图2,窗户从开到最大到关闭( , , , 与 重合)的过程中,控制臂 , 带动 上的滑块 向点 滑动了 .则 的长为 .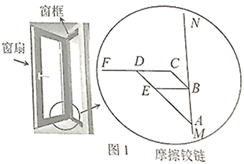

三、解答题
-
19.(1)、计算:(2)、解方程:20. 如图,16个形状大小完全相同的菱形组成网格 ,菱形的顶点称为格点.
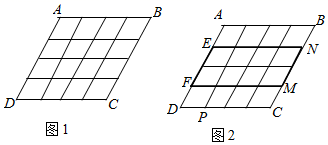 (1)、在图1中画出矩形 ,使得 , , , 分别落在 , , , 边(包含端点)的格点上;(2)、如图2,已知点 , , , , 均在格点上,请在网格中(包含边界)找一格点 ,连结 ,使得直线 平分 的面积.21. 2019年起温州开始实施垃圾分类,生活垃圾可分为“可回收物”、“有害垃圾”、“易腐垃圾”、“其他垃级”四大类.为合理安排垃圾车运输生活垃圾,工作人员从某街道500个垃圾投放点中随机抽取10个,对每日垃圾投放量进行调查.整理得到以下信息:
(1)、在图1中画出矩形 ,使得 , , , 分别落在 , , , 边(包含端点)的格点上;(2)、如图2,已知点 , , , , 均在格点上,请在网格中(包含边界)找一格点 ,连结 ,使得直线 平分 的面积.21. 2019年起温州开始实施垃圾分类,生活垃圾可分为“可回收物”、“有害垃圾”、“易腐垃圾”、“其他垃级”四大类.为合理安排垃圾车运输生活垃圾,工作人员从某街道500个垃圾投放点中随机抽取10个,对每日垃圾投放量进行调查.整理得到以下信息:(信息一)10个投放点“可回收物”每日投放量(单位: )数据如下:
170,188,181,170,179,182,170,190,170,200
(信息二)10个投放点各类垃圾每日投放量的平均数、中位数、众数(单位: )数据如下(部分空缺):
各类垃圾
平均数
中位数
众数
可回收物
▲
180
170
有害垃圾
10
15
13
易腐垃圾
260
280
281
其他垃圾
100
102
100
(1)、求10个投放点“可回收物”每日投放量的平均数;(2)、若每辆垃圾车可以运输5吨生活垃圾,请选择恰当统计量估计该街道每天需要安排多少辆垃圾车才能将500个垃圾投放点的全部生活垃圾运走.22. 如图,点 , 分别在反比例函数 , 在第一象限的图象上,点 是 轴正半轴上一点,连结 , , .已知四边形 是平行四边形,且 , 两点的纵坐标之比为 .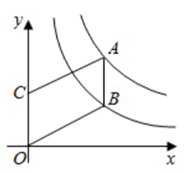 (1)、求 的值;(2)、当 是菱形时,求 的长.23. 疫情期间,某公司向厂家订购 , 两款洗手液共50箱,已知购买 款洗手液1箱进价为200元,在此基础上,所购买的 款洗手液数量每增加1箱,每箱进价降低2元.厂家为保障盈利,每次最多可订购30箱 款洗手液. 款洗手液的进价为每箱100元.设该公司购买 款洗手液 箱.(1)、根据信息填表:
(1)、求 的值;(2)、当 是菱形时,求 的长.23. 疫情期间,某公司向厂家订购 , 两款洗手液共50箱,已知购买 款洗手液1箱进价为200元,在此基础上,所购买的 款洗手液数量每增加1箱,每箱进价降低2元.厂家为保障盈利,每次最多可订购30箱 款洗手液. 款洗手液的进价为每箱100元.设该公司购买 款洗手液 箱.(1)、根据信息填表:型号
数量(箱)
进价(元/箱)
100
(2)、若订购这批洗手液的总进价为6240元,则该公司订购了多少箱 款洗手液?24. 如图,在矩形 中, ,点 是边 的中点.连结 , , 分别是射线 , 上的动点,且 .连结 , .过点 , 分别作 , 的平行线交于点 .
 (1)、当点 在线段 上(不包含端点)时;
(1)、当点 在线段 上(不包含端点)时;①求证:四边形 是正方形;
②若 将四边形 的面积分为 两部分,求 的长;
(2)、如图2,连结 ,若点 在对角线 上,求 的面积(直接写出答案).