浙江省宁波市北仑区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-08-24 类型:期末考试
一、单选题
-
1. 五边形的内角和是( )A、180° B、360° C、540° D、720°2. 下列计算正确的为( )A、 B、 C、 D、3. 下列各图中,不是中心对称图形的为( )A、
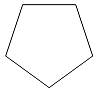 B、
B、 C、
C、 D、
D、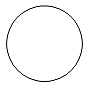 4. 用反证法证明“a≥b”时应先假设( )A、a≤b B、a>b C、a<b D、a≠b5. 在某次考试后,组办方对应聘者进行了“听、说、读、写”四项技能测试,若人才要求是具有强的“听”力.较强的“说”与“写”能力及基本的“读”能力,根据这个要求,“听、说、读、写”四项技能测试比较合适的权重设计为( )A、3:3:2:2 B、5:2:1:2 C、1:2:2:5 D、2:3:3:26. 一元二次方程x2﹣3 x+6=0的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根7. 在平面直角坐标系中,菱形ABCD的顶点的坐标A,B,C分别为(﹣2,0),(0,1),(2,0),则顶点D的坐标为( )A、(0,﹣1) B、(﹣2,1) C、(2,1) D、(0,﹣2)8. 为了美化校园环境,某区第一季度用于绿化的投资为18万元,前三个季度用于绿化的总投资为90万元,设前三个季度用于绿化投资的平均增长率为x.那么x满足的方程为( )A、18 (1+2x)=90 B、18 (1+x) 2=90 C、18+18 (1+x)+18 (1+2x)=90 D、18+18 (1+x)+18 (1+x) 2=909. 如图,四边形ABCD中.AC⊥BC,AD∥BC,BD为∠ABC的平分线,BC=3,AC=4.E,F分别是BD,AC的中点,则EF的长为( )
4. 用反证法证明“a≥b”时应先假设( )A、a≤b B、a>b C、a<b D、a≠b5. 在某次考试后,组办方对应聘者进行了“听、说、读、写”四项技能测试,若人才要求是具有强的“听”力.较强的“说”与“写”能力及基本的“读”能力,根据这个要求,“听、说、读、写”四项技能测试比较合适的权重设计为( )A、3:3:2:2 B、5:2:1:2 C、1:2:2:5 D、2:3:3:26. 一元二次方程x2﹣3 x+6=0的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根7. 在平面直角坐标系中,菱形ABCD的顶点的坐标A,B,C分别为(﹣2,0),(0,1),(2,0),则顶点D的坐标为( )A、(0,﹣1) B、(﹣2,1) C、(2,1) D、(0,﹣2)8. 为了美化校园环境,某区第一季度用于绿化的投资为18万元,前三个季度用于绿化的总投资为90万元,设前三个季度用于绿化投资的平均增长率为x.那么x满足的方程为( )A、18 (1+2x)=90 B、18 (1+x) 2=90 C、18+18 (1+x)+18 (1+2x)=90 D、18+18 (1+x)+18 (1+x) 2=909. 如图,四边形ABCD中.AC⊥BC,AD∥BC,BD为∠ABC的平分线,BC=3,AC=4.E,F分别是BD,AC的中点,则EF的长为( ) A、1 B、1.5 C、2 D、2.510. 定义新运算:a※b= ,则函数y=4※x的图象可能为( )A、
A、1 B、1.5 C、2 D、2.510. 定义新运算:a※b= ,则函数y=4※x的图象可能为( )A、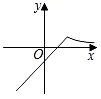 B、
B、 C、
C、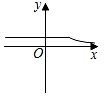 D、
D、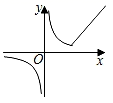
二、填空题
-
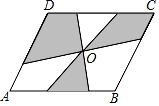
11. 二次根式 中字母 的取值范围是12. 已知一组数据为:3,x,6,5,4,若这组数据的众数是4,则x的值为.13. 若x=4是二次方程x2+ax﹣4b=0的解,则代数式a﹣b的值为.14. 在平面直角坐标系中,正比例函数y=3x与反比例函数y= 的图象交于点A(a,﹣6),则k=.15. 如图,菱形ABCD中,O是两条对角线的交点,过点O的三条直线将菱形分成阴影部分和空白部分,当菱形的边长为10,一条对角线为12时,则阴影部分的面积为.
 16. 如图,平行四边形ABCD中,点O是对角线AC的中点,点M为BC上一点,连接AM,且AB=AM,点E为BM中点,AF⊥AB,连接EF,延长FO交AB于点N,∠ACB=45°,AN=1,AF=3,则EF=.
16. 如图,平行四边形ABCD中,点O是对角线AC的中点,点M为BC上一点,连接AM,且AB=AM,点E为BM中点,AF⊥AB,连接EF,延长FO交AB于点N,∠ACB=45°,AN=1,AF=3,则EF=.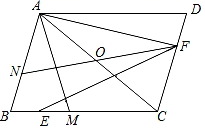
三、解答题
-
17. 计算:(1)、 ;(2)、 .18. 解方程:(1)、(x﹣4)2﹣3=0;(2)、4(x﹣3)=2x(x﹣3).19. 某射击队伍正在进行射击训练,现有两位选手的5次射击成绩如下所示:
甲:7环,8环,9环,8环,10环
乙:6环,9环,10环,8环,10环
(1)、分别求甲、乙两位选手的射击成绩的中位数和众数;(2)、经过计算甲的方差为1.04环2 , 乙的方差为2.24环2.所以选手更加稳定.20. 如图,已知点A(2,m)是反比例函数y= 的图象上一点,过点A作x轴的垂线,垂足为B,连结OA,△ABO的面积为6.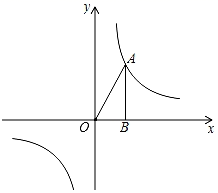 (1)、求k和m的值;(2)、直线y=2x+a(a≤0)与直线AB交于点C与反比例函数图象交于点E,F;
(1)、求k和m的值;(2)、直线y=2x+a(a≤0)与直线AB交于点C与反比例函数图象交于点E,F;①若a=0,已知E(p,q),则F的坐标为▲(用含p,q的坐标表示);
②若a=﹣2.求AC的长.
21. 已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE = AF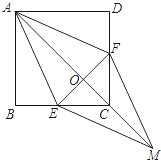 (1)、求证:BE = DF;(2)、连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.22. 疫情结束后,某广场推出促销活动,已知商品每件的进货价为30元,经市场调研发现,当该商品的销售单价为40元时,每天可销售280件;当销售单价每增加1元,每天的销售数量将减少10件.(销售利润=销售总额﹣进货成本).(1)、若该商品的的件单价为43元时,则当天的售商品是件,当天销售利润是元;(2)、当该商品的销售单价为多少元时,该商品的当天销售利润是3450元.23. 小王为探究函数y= (x>3)的图象经历了如下过程.
(1)、求证:BE = DF;(2)、连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.22. 疫情结束后,某广场推出促销活动,已知商品每件的进货价为30元,经市场调研发现,当该商品的销售单价为40元时,每天可销售280件;当销售单价每增加1元,每天的销售数量将减少10件.(销售利润=销售总额﹣进货成本).(1)、若该商品的的件单价为43元时,则当天的售商品是件,当天销售利润是元;(2)、当该商品的销售单价为多少元时,该商品的当天销售利润是3450元.23. 小王为探究函数y= (x>3)的图象经历了如下过程. (1)、列表,根据表中x的取值,求出对应的y值,将空白处填写完整;
(1)、列表,根据表中x的取值,求出对应的y值,将空白处填写完整;x
…
3.5
4
4.5
5
5.5
6
…
y
…
3
2
1
…
(2)、以表中各组对应值为点的坐标,在平面直角坐标系中描点并画出函数图象;(3)、结合由y= (x>0)图象到y= 图象的变化,猜想由y= 的图象经过向的平移变化可以得到y= (x≠﹣3)图象.y= (x≠﹣3)的对称轴是.24.(1)、如图1,四边形ACDE中,△ABC与△BDE均为直角三角形,且AB⊥BE,∠BEA=45°,求证:△ABC≌△BED.
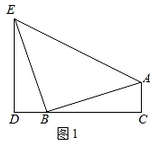 (2)、如图2,点A(1,2),连结OA,将射线OA绕点O按逆时针方方向旋转45°.得到射线OB,AC⊥OA交OB于点C,分别过点A,点C作x轴,AD的垂线,垂足分别为D,E,由(1)得(填写两个三角形全等),所以CE= , AE= , C的坐标为 , 则直线OB的解析式为.
(2)、如图2,点A(1,2),连结OA,将射线OA绕点O按逆时针方方向旋转45°.得到射线OB,AC⊥OA交OB于点C,分别过点A,点C作x轴,AD的垂线,垂足分别为D,E,由(1)得(填写两个三角形全等),所以CE= , AE= , C的坐标为 , 则直线OB的解析式为.
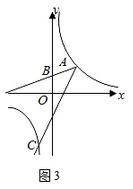
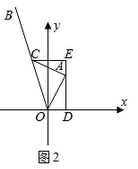 (3)、如图3,点A(3,3)在反比例函数y= 的图象上,B(0,2)作射线AB,将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象的另一支于点C,求点C的坐标.
(3)、如图3,点A(3,3)在反比例函数y= 的图象上,B(0,2)作射线AB,将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象的另一支于点C,求点C的坐标.
 25. 如图1,在平面直角坐标系xOy中,直线AB:y=kx+b(b≠0)分别与y轴,x轴交于A,B两点,点E,点G分别为AB,OE中点,点A,B关于点G的对称点分别为C,D,则称四边形ABCD为直线AB的伴随四边形,直线CD为直线AB的伴随直线.
25. 如图1,在平面直角坐标系xOy中,直线AB:y=kx+b(b≠0)分别与y轴,x轴交于A,B两点,点E,点G分别为AB,OE中点,点A,B关于点G的对称点分别为C,D,则称四边形ABCD为直线AB的伴随四边形,直线CD为直线AB的伴随直线.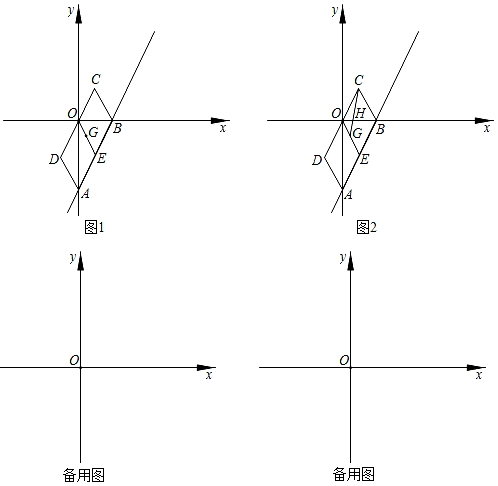 (1)、若伴随四边形为矩形,则k=;(2)、已知伴随直线为y=﹣4x,四边形ABCD的面积为25,求直线AB的解析式;(3)、如图2,连结CG,与x轴交于点H,若△BHC为等腰三角形且k>0,求k的值.
(1)、若伴随四边形为矩形,则k=;(2)、已知伴随直线为y=﹣4x,四边形ABCD的面积为25,求直线AB的解析式;(3)、如图2,连结CG,与x轴交于点H,若△BHC为等腰三角形且k>0,求k的值.