重庆市渝中区2019-2020学年七年级下学期数学期末考试试卷
试卷更新日期:2020-08-24 类型:期末考试
一、选择题
-
1. 下列实数中,无理数为( )A、-1 B、0 C、 D、2. 如图, ∠1与∠2的关系是( )
 A、对顶角 B、同位角 C、内错角 D、同旁内角3. 下列计算正确的是( )A、 B、 C、 D、4. 下列各组数中,是方程 的解的为( )A、 B、 C、 D、5. 下列图形中,不能由“基本图案”(小四边形)经过平移得到的图形为( )A、
A、对顶角 B、同位角 C、内错角 D、同旁内角3. 下列计算正确的是( )A、 B、 C、 D、4. 下列各组数中,是方程 的解的为( )A、 B、 C、 D、5. 下列图形中,不能由“基本图案”(小四边形)经过平移得到的图形为( )A、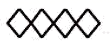 B、
B、 C、
C、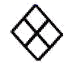 D、
D、 6. 若a>b,则下列不等式成立的是( )A、 B、 C、 D、7. 某校为了解疫情期向3000名学生网上学习的效果,随机抽取了300名学生网上学习效果的检测情况进行统计分析.其中样本容量为( )A、3000名学生网上学习的效果 B、3000 C、抽取的300名学生网上学习的效果 D、3008. 估计 的值在( )A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间9. 如图,有四个条件:① ;② ;③ ;④ .其中能判定 的条件有( )
6. 若a>b,则下列不等式成立的是( )A、 B、 C、 D、7. 某校为了解疫情期向3000名学生网上学习的效果,随机抽取了300名学生网上学习效果的检测情况进行统计分析.其中样本容量为( )A、3000名学生网上学习的效果 B、3000 C、抽取的300名学生网上学习的效果 D、3008. 估计 的值在( )A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间9. 如图,有四个条件:① ;② ;③ ;④ .其中能判定 的条件有( )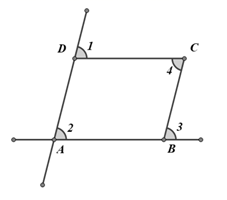 A、1个 B、2个 C、3个 D、4个10. 无论x取何值,点P (x+2, x-1)都不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限11. 我国古代数学名著《九章算术》中记载有这样一道题:“今有二马、一牛价过一万,如半马之价;一马二牛价不满一万,如半牛之价.1问牛、马价各几何?”其大意是:今有2匹马、1头牛的总价超过10000钱,其超出的钱数相当于 匹马的价格;1匹马、2头牛的总价不足1000钱,所差的钱数相当于 头牛的价格.问每头牛、每匹马的价格各是多少?若设每头牛的价格为x钱,每匹马的价格为y钱,则根据题意列方程组正确的为 ( )A、 B、 C、 D、12. 在平面直角坐标系中,对任意两点 、 .规定运算如下:① ;② ;③当 且 时,称A=B.则下面命题是假命题的为( )A、若A(-1, 2), B(2, 1), 则A B=(1, 3), A B=0 B、若三点 、 、 满足 则A=C C、若三点 、 、 满足 则A=C D、三点 、 、 ,恒有 成立
A、1个 B、2个 C、3个 D、4个10. 无论x取何值,点P (x+2, x-1)都不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限11. 我国古代数学名著《九章算术》中记载有这样一道题:“今有二马、一牛价过一万,如半马之价;一马二牛价不满一万,如半牛之价.1问牛、马价各几何?”其大意是:今有2匹马、1头牛的总价超过10000钱,其超出的钱数相当于 匹马的价格;1匹马、2头牛的总价不足1000钱,所差的钱数相当于 头牛的价格.问每头牛、每匹马的价格各是多少?若设每头牛的价格为x钱,每匹马的价格为y钱,则根据题意列方程组正确的为 ( )A、 B、 C、 D、12. 在平面直角坐标系中,对任意两点 、 .规定运算如下:① ;② ;③当 且 时,称A=B.则下面命题是假命题的为( )A、若A(-1, 2), B(2, 1), 则A B=(1, 3), A B=0 B、若三点 、 、 满足 则A=C C、若三点 、 、 满足 则A=C D、三点 、 、 ,恒有 成立二、填空题
-
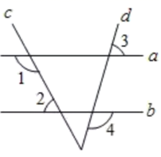
13. 的立方根是 .14. “a的一半与1的差不大于5”用不等式表示为.15. 如图, 已知 , ,则 .
 16. 在平面直角坐标系中,已知线段MN//x轴,且MN=3,若点M的坐标为(-2,1),则点N的坐标为.17. 已知a-2b的平方根是 ,a+3b的立方根是-1,则a+b=.18. 在一个盒子中装有若干乒乓球,小明为了探究盒子中所装乒乓球的数量,他先从盒子中取出一些乒乓球,记录了所取乒乓球的数量为m个,并在这些乒乓球上做了记号“*”,然后将它们放回盒子中,充分摇匀;接下来,他又从这个盒子中再次取出一些乒乓球,记录了所取乒乓球的数量为n个,其中带有记号“*”的乒乓球有p个,小明根据实验所得的数据m、n、p,可估计出盒子中乒乓球的数量有个.
16. 在平面直角坐标系中,已知线段MN//x轴,且MN=3,若点M的坐标为(-2,1),则点N的坐标为.17. 已知a-2b的平方根是 ,a+3b的立方根是-1,则a+b=.18. 在一个盒子中装有若干乒乓球,小明为了探究盒子中所装乒乓球的数量,他先从盒子中取出一些乒乓球,记录了所取乒乓球的数量为m个,并在这些乒乓球上做了记号“*”,然后将它们放回盒子中,充分摇匀;接下来,他又从这个盒子中再次取出一些乒乓球,记录了所取乒乓球的数量为n个,其中带有记号“*”的乒乓球有p个,小明根据实验所得的数据m、n、p,可估计出盒子中乒乓球的数量有个.三、解答题
-
19. 计算:(1)、 ;(2)、20. 解下列方程组:(1)、(2)、21. 园林部门为了对市内某旅游景区内的古树名木进行系统养护,建立了相关的地理信息系统,其中重要的一项工作就是要确定这些古树的位置.已知该旅游区有树龄百年以上的古松树4棵 ,古槐树6棵 .为了加强对这些古树的保护,园林部门根据该旅游景区地图,将4棵古松树的位置用坐标表示为S1(2,8),S2(4, 9),S3(10, 5),S4(11,10).
 (1)、根据S1的坐标为(2, 8),请在图中补充画出平面直角坐标系;(2)、在所建立的平面直角坐标系中,写出6棵古槐树的坐标;(3)、已知H5在S1 , 的南偏东41°,且相距5.4米处,试用方位角和距离描述S1;相对于H5的位置?22. 如图,已知AB//CD,直线EF与AB、CD相交于H、F两点,FG平分∠EFD.
(1)、根据S1的坐标为(2, 8),请在图中补充画出平面直角坐标系;(2)、在所建立的平面直角坐标系中,写出6棵古槐树的坐标;(3)、已知H5在S1 , 的南偏东41°,且相距5.4米处,试用方位角和距离描述S1;相对于H5的位置?22. 如图,已知AB//CD,直线EF与AB、CD相交于H、F两点,FG平分∠EFD.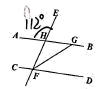 (1)、若∠AHE=112°,求∠EFG和∠FGB的度数;(2)、若∠AHE=n°,请直接写出∠EFG和∠FGB的度数.23. 在抗击新冠疫情期间,市教委组织开展了“停课不停学”的活动.为了解此项活动的开展情况,市教委督导部门准备采用以下调查方式中的一种进行调查:
(1)、若∠AHE=112°,求∠EFG和∠FGB的度数;(2)、若∠AHE=n°,请直接写出∠EFG和∠FGB的度数.23. 在抗击新冠疫情期间,市教委组织开展了“停课不停学”的活动.为了解此项活动的开展情况,市教委督导部门准备采用以下调查方式中的一种进行调查:A.从某所普通中学校随机选取200名学生作为调查对象进行调查;
B.从市内某区的不同学校中随机选取200名学生作为调查对象进行调查;
C.从市教育部门学生学籍档案中随机抽取200名学生作为调查对象进行调查.
 (1)、在上述调查方式中,你认为比较合理的一个是(填番号).(2)、如图,是按照一种比较合理的调查方式所得到的数据制成的频数分布直方图,在这个调查中,所抽取200名学生每天“停课不停学”的学习时间在1~2小时之间的人数m=.(3)、已知全市共有100万学生,请你利用(2)问中的调查结果,估计全市每天“停课不停学”的学习时间在1~2小时及以上的人数有多少?(4)、你认为这个调查活动的设计有没有不合理的地方?谈谈你的理由.24. 已知不等式组 有且只有两个整数解,求实数a的取值范围,并用数轴把它表示出来.25. 如图①,已知AB//CD, AC//EF
(1)、在上述调查方式中,你认为比较合理的一个是(填番号).(2)、如图,是按照一种比较合理的调查方式所得到的数据制成的频数分布直方图,在这个调查中,所抽取200名学生每天“停课不停学”的学习时间在1~2小时之间的人数m=.(3)、已知全市共有100万学生,请你利用(2)问中的调查结果,估计全市每天“停课不停学”的学习时间在1~2小时及以上的人数有多少?(4)、你认为这个调查活动的设计有没有不合理的地方?谈谈你的理由.24. 已知不等式组 有且只有两个整数解,求实数a的取值范围,并用数轴把它表示出来.25. 如图①,已知AB//CD, AC//EF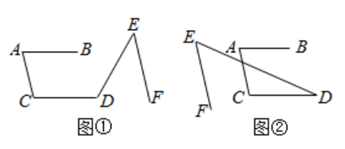 (1)、若∠A=75°, ∠E=45°,求∠C和∠CDE的度数;(2)、探究:∠A、∠CDE与∠E之间有怎样的等量关系?并说明理由.(3)、若将图①变为图②,题设的条件不变,此时∠A、∠CDE 与∠E之间又有怎样的等量关系,请直接写出你探究的结论.26. 武汉新冠肺炎疫情发生后,全国人民众志成诚抗疫救灾.某公司筹集了抗疫物资120吨打算运往武汉疫区,现有甲、乙、两三种车型供运输选择,每辆车的运载能力和运费如下表所示: (假设每辆车均满载)
(1)、若∠A=75°, ∠E=45°,求∠C和∠CDE的度数;(2)、探究:∠A、∠CDE与∠E之间有怎样的等量关系?并说明理由.(3)、若将图①变为图②,题设的条件不变,此时∠A、∠CDE 与∠E之间又有怎样的等量关系,请直接写出你探究的结论.26. 武汉新冠肺炎疫情发生后,全国人民众志成诚抗疫救灾.某公司筹集了抗疫物资120吨打算运往武汉疫区,现有甲、乙、两三种车型供运输选择,每辆车的运载能力和运费如下表所示: (假设每辆车均满载)车型
甲
乙
丙
运载量(吨/辆)
5
8
10
运费(元/辆)
450
600
700
(1)、全部物资一次性运送可用甲型车8辆,乙型车5辆,丙型车辆.(2)、若全部物资仅用甲、乙两种车型一次性运完,需运费9600元,求甲、乙两种车型各需多少辆?(3)、若该公司打算用甲、乙、丙三种车型同时参与运送,已知车辆总数为14辆,且一次性运完所有物资,你能分别求出三种车型的辆数吗?此时的总运费为多少元?