重庆市四区2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2020-08-24 类型：期末考试

进入出卷网下载

一、选择题

1. 若关于x的方程3(x＋k)＝x＋6的解是非负数，则k的取值范围是（）

A、k≥2 B、k＞2 C、k≤2 D、k＜2

查看试题解析
2. 已知 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ 是方程组 ${\begin{array}{l} a x + b y = 5 \\ b x + a y = 1 \end{array}$ 的解，则 $3 - a - b$ 的值是（）

A、–1 B、1 C、2 D、3

查看试题解析
3. 如果点P（3﹣m，1）在第二象限，那么关于x的不等式（2﹣m）x+2＞m的解集是（　　）

A、x＞﹣1 B、x＜﹣1 C、x＞1 D、x＜1

查看试题解析
4. 在平行四边形 $A B C D$ 中， $∠ B = 30^{\circ}$ ， $C D = 2 \sqrt{3}$ ， $B C = 2$ ，则平行四边形 $A B C D$ 的面积等于（）

A、 $2 \sqrt{3}$ B、4 C、 $4 \sqrt{3}$ D、6

查看试题解析
5. 如图所示，光线L照射到平面镜I上，然后在平面镜Ⅰ、Ⅱ之间来回反射，已知∠α=55°，∠γ=75°，则∠β为（）

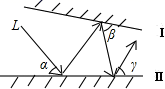A、50° B、55° C、60° D、65°

查看试题解析
6. 已知关于x的方程（5a+14b）x+6＝0无解，则ab是（）

A、正数 B、非负数 C、负数 D、非正数

查看试题解析
7. 已知关于x，y的方程组 ${\begin{array}{l} 3 x - 5 y = 2 a \\ x - 2 y = a - 5 \end{array}$ ，则下列结论中正确的是（）
①当a＝5时，方程组的解是 ${\begin{array}{l} x = 10 \\ y = 20 \end{array}$ ；②当x，y的值互为相反数时，a＝20；③当 $2^{x} \cdot 2^{y} = 16$ 时，a＝18；④不存在一个实数a使得x=y.

A、①②④ B、②③④ C、②③ D、②④

查看试题解析
8. 某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到敬老院慰问老人.如果分给每位老人4盒牛奶，那么剩下28盒牛奶；如果分给每位老人5盒牛奶，那么最后一位老人分得的牛奶不足4盒，但至少1盒.则这个敬老院的老人最少有（ )

A、29人 B、30人 C、31人 D、32人

查看试题解析
9. 一个多边形截去一个角(不过顶点)后，所成的一个多边形的内角和是2520°，那么原多边形的边数是（）

A、13 B、15 C、17 D、19

查看试题解析
10. 如图，在5×5的正方形网格中已有5块被涂成阴影，则在未涂的空格中，任选一格涂成阴影，可使阴影部分为轴对称图形的概率是（）

A、 $\frac{1}{10}$ B、 $\frac{3}{20}$ C、 $\frac{1}{5}$ D、 $\frac{1}{4}$

查看试题解析
11. 如图，矩形ABCD中，AB＝2 $\sqrt{3}$ ，BC＝6，P为矩形内一点，连接PA，PB，PC，则PA+PB+PC的最小值是（）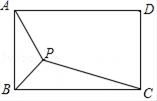

A、4 $\sqrt{3}$ +3 B、2 $\sqrt{21}$ C、2 $\sqrt{3}$ +6 D、4 $\sqrt{5}$

查看试题解析
12. 若关于x的一元一次不等式组 ${\begin{array}{l} x - \frac{1}{4} (4 a - 2) \leq \frac{1}{2} \\ \frac{3 x - 1}{2} < x + 2 \end{array}$ 的解集是x $\leq$ a，且关于y的分式方程 $\frac{2 y - a}{y - 1} - \frac{y - 4}{1 - y} = 1$ 有非负整数解，则符合条件的所有整数a的和为（）

A、0 B、1 C、4 D、6

查看试题解析

二、填空题

13. 若关于x的方程 $3 x - 5 = x + 2 m$ 的解为 $x = 2$ ，则m的值为．

查看试题解析
14. 《孙子算经》中记载了一道题，大意是：100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，问有多少匹大马、多少匹小马？设有x匹大马，y匹小马，根据题意可列方程组为．

查看试题解析
15. 如果不等式 $(2 a - 1) x > 1$ 的解集是 $x < \frac{1}{2 a - 1}$ ，那么a的取值范围是.

查看试题解析
16. 如图，在平面直角坐标系中，以点A（0，2）为圆心，2为半径的圆交y轴于点B.已知点C（2，0），点D为⊙A上的一动点，以CD为斜边，在CD左侧作等腰直角三角形CDE，连结BC，则△BCE面积的最小值为.

查看试题解析
17. 如图，在△ABC中，E是BC上的一点，EC=2BE，点D是AC的中点，设△ABC、△ADF、△BEF的面积分别S、S₁、S₂ ，且S=36，则S₁-S₂=.

查看试题解析
18. 如图，将直线y＝x向下平移b个单位长度后得到直线l ， l与反比例函数y＝ $\frac{5}{x}$ （x＞0）的图象相交于点A ，与x轴相交于点B ，则OA²﹣OB²的值为．

查看试题解析

三、解答题

19. 计算

(1)、计算： $\frac{3}{\sqrt{3}} - {(π - 3)}^{0} + {(- \frac{1}{2})}^{- 1} - \sqrt{27} + | \sqrt{3} - 2 |$

(2)、解方程组 ${\begin{array}{l} x - 2 y + 3 z = 0 \\ 3 x + 2 y + 5 z = 12 \\ 2 x - 4 y - z = - 7 \end{array}$

查看试题解析
20. 如图，∠B=42°，∠1=∠2+10°，∠ACD=64°，∠ACD的平分线与BA的延长线相交于点E.

(1)、请你判断BF与CD的位置关系，并说明理由；

(2)、求∠3的度数.

查看试题解析
21. 如图，已知 $△ A B C$ 和 $△ A E F$ 中， $∠ B = ∠ E$ ， $A B = A E$ ， $B C = E F$ ， $∠ E A B = 25^{\circ}$ ， $∠ F = 57^{\circ}$ ；

(1)、请说明 $∠ E A B = ∠ F A C$ 的理由；

(2)、 $△ A B C$ 可以经过图形的变换得到 $△ A E F$ ，请你描述这个变换；

(3)、求 $∠ A M B$ 的度数.

查看试题解析
22. 仙桃是遂宁市某地的特色时令水果．仙桃一上市，水果店的老板用2400元购进一批仙桃，很快售完；老板又用3700元购进第二批仙桃，所购件数是第一批的 $\frac{3}{2}$ 倍，但进价比第一批每件多了5元．

(1)、第一批仙桃每件进价是多少元？

(2)、老板以每件225元的价格销售第二批仙桃，售出80%后，为了尽快售完，剩下的决定打折促销．要使得第二批仙桃的销售利润不少于440元，剩余的仙桃每件售价至少打几折？（利润＝售价﹣进价）

查看试题解析
23. 小碚向某校食堂王经理建议食堂就餐情况，经调查发现就餐时，有520人排队吃饭就餐，就餐开始后仍有学生继续前来排队进食堂.设学生按固定的速度增加，食堂打饭窗口打饭菜的速度也是固定的.若每分钟该食堂新增排队学生数12人，每个打饭窗口1每分钟打饭菜10人.已知食堂的前a分钟只开放了两个打饭窗口；某一天食堂排队等候的学生数y（人）与打饭菜时间x（分钟）的关系如图所示.

(1)、求a的值；

(2)、求排队到第16分钟时，食堂排队等候打饭菜的学生人数；

(3)、若要在开始打饭菜后8分钟内让所有排队的学生都能进食堂后来到食堂窗口的学生随到随吃，那么小碚应该建议食堂王经理一开始就需要至少同时开放几个打饭窗口？

查看试题解析
24. 如图1，已知锐角△ABC中，CD、BE分别是AB、AC边上的高，M、N分别是线段BC、DE的中点.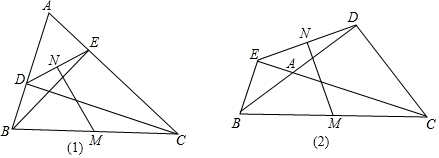

(1)、求证：MN⊥DE.

(2)、连结DM，ME，猜想∠A与∠DME之间的关系，并证明猜想.

(3)、当∠A变为钝角时，如图2，上述（1）（2）中的结论是否都成立，若结论成立，直接回答，不需证明；若结论不成立，说明理由.

查看试题解析
25. 阅读下列材料：
我们知道 $| x |$ 的几何意义是在数轴上数x对应的点与原点的距离；即 $| x | = | x - 0 |$ ；这个结论可以推广为 $| x_{1} - x_{2} |$ 表示在数轴上数 $x_{1}$ ， $x_{2}$ 对应点之间的距离.绝对值的几何意义在解题中有着广泛的应用：

例1：解方程 $| x | = 4$ .

容易得出，在数轴上与原点距离为4的点对应的数为±4，即该方程的 $x =$ ±4；

例2：解方程 $| x + 1 | + | x - 2 | = 5$ .

由绝对值的几何意义可知，该方程表示求在数轴上与-1和2的距离之和为5的点对应的x的值.在数轴上，-1和2的距离为3，满足方程的x对应的点在2的右边或在-1的左边.若x对应的

点在2的右边，如图可以看出 $x = 3$ ；同理，若x对应点在-1的左边，可得 $x = - 2$ .所以原方程的解是 $x = 3$ 或 $x = - 2$ .

例3：解不等式 $| x - 1 | > 3$ .

在数轴上找出 $| x - 1 | = 3$ 的解，即到1的距离为3的点对应的数为-2，4，如图，在-2的左边或在4的右边的 $x$ 值就满足 $| x - 1 | > 3$ ，所以 $| x - 1 | > 3$ 的解为 $x < - 2$ 或 $x > 4$ .

参考阅读材料，解答下列问题：

(1)、方程 $| x + 3 | = 5$ 的解为；

(2)、方程 $| x - 2017 | + | x + 1 | = 2020$ 的解为；

(3)、若 $| x + 4 | + | x - 3 | \geq 11$ ，求x的取值范围.

查看试题解析
26. 小华将一张矩形纸片（如图1）沿对角线CA剪开，得到两张三角形纸片（如图2），其中∠ACB=α，然后将这两张三角形纸片按如图3所示的位置摆放，△EFD纸片的直角顶点D落在△ACB纸片的斜边AC上，直角边DF落在AC所在的直线上.

(1)、若ED与BC相交于点G，取AG的中点M，连接MB、MD，当△EFD纸片沿CA方向平移时（如图3），请你观察、测量MB、MD的长度，猜想并写出MB与MD的数量关系，然后证明你的猜想；

(2)、在（1）的条件下，求出∠BMD的大小（用含α的式子表示），并说明当α=45°时，△BMD是什么三角形；

(3)、在图3的基础上，将△EFD纸片绕点C逆时针旋转一定的角度（旋转角度小于90°），此时△CGD变成△CHD，同样取AH的中点M，连接MB、MD（如图4），请继续探究MB与MD的数量关系和∠BMD的大小，直接写出你的猜想，不需要证明，并说明α为何值时，△BMD为等边三角形.

查看试题解析