浙江省嘉兴市2019-2020学年七年级下学期数学期末考试试卷
试卷更新日期:2020-08-24 类型:期末考试
一、选择题
-
1. 计算 的结果是( )A、 B、 C、 D、2. 如图,下列四个角中,与∠1构成一对同位角的是( )
 A、∠2 B、∠3 C、∠4 D、∠53. 下列调查中,适宜全面调查的是( )A、了解某班学生的视力情况 B、了解某批次汽车的抗撞击能力 C、了解春节联欢晚会的收视率 D、了解池塘中现有鱼的数量4. 新型冠状病毒属冠状病毒属,冠状病毒科,体积很小,最大直径不超过140纳米(即0.00000014米).数0.00000014用科记计数法表示为( )A、 B、 C、 D、5. 下列由左边到右边的变形中,属于因式分解的是( )A、 B、 C、 D、6. 下列某个方程与 组成方程组的解为 ,则这个方程是( )A、 B、 C、 D、7. 如图,在边长为1的小正力形组成的网格中,点A,B,C部在格点上,若将线段AB沿BC方向平移,使点B与点C重合,则线段AB扫过的面积为( )
A、∠2 B、∠3 C、∠4 D、∠53. 下列调查中,适宜全面调查的是( )A、了解某班学生的视力情况 B、了解某批次汽车的抗撞击能力 C、了解春节联欢晚会的收视率 D、了解池塘中现有鱼的数量4. 新型冠状病毒属冠状病毒属,冠状病毒科,体积很小,最大直径不超过140纳米(即0.00000014米).数0.00000014用科记计数法表示为( )A、 B、 C、 D、5. 下列由左边到右边的变形中,属于因式分解的是( )A、 B、 C、 D、6. 下列某个方程与 组成方程组的解为 ,则这个方程是( )A、 B、 C、 D、7. 如图,在边长为1的小正力形组成的网格中,点A,B,C部在格点上,若将线段AB沿BC方向平移,使点B与点C重合,则线段AB扫过的面积为( )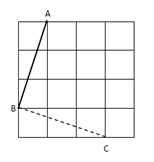 A、11 B、10 C、9 D、88. 已知, , ,则代数式 的值是( )A、5 B、-5 C、6 D、-69. 按如图所示的程序计算,若 ,则 的结果为( )
A、11 B、10 C、9 D、88. 已知, , ,则代数式 的值是( )A、5 B、-5 C、6 D、-69. 按如图所示的程序计算,若 ,则 的结果为( )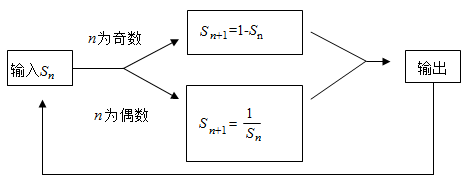 A、a B、 C、 D、
A、a B、 C、 D、二、填空题
-
10. 若分式 有意义,则x的取值范围为11. 计算 .12. 因式分解: =.13. 若关于x,y的方程 是一个二元一次方程,则m的值为.14. 公益活动中,小明根据本班同学的捐款情况绘制成如图所示的不完整统计图,期中捐10元的人数占全班总人数的40%,则本次捐款20元的人数为人.
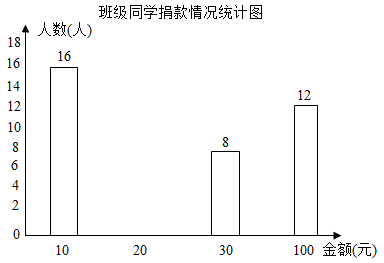 15. 如图,将一副三角板和一张对边平行的纸条按如图方式摆放,则∠α的度数是.
15. 如图,将一副三角板和一张对边平行的纸条按如图方式摆放,则∠α的度数是. 16. 已知 (y≠1),若用含x的代数式表示y,则y=.17. 设 , ,若 ,则 的值为.18. 若 , ,则 的值为.19. 如图,在长方形ABCD中,AB<BC,点P为长方形内部一点,过点P分别作PE⊥BC于点E、PF⊥CD于点F,分别以PF、CF为边作正方形PMNF,正方形GHCF,若两个正方形的面积之和为42,长方形PECF的面积为11,BE=DF=2,则长方形ABCD的面积为.
16. 已知 (y≠1),若用含x的代数式表示y,则y=.17. 设 , ,若 ,则 的值为.18. 若 , ,则 的值为.19. 如图,在长方形ABCD中,AB<BC,点P为长方形内部一点,过点P分别作PE⊥BC于点E、PF⊥CD于点F,分别以PF、CF为边作正方形PMNF,正方形GHCF,若两个正方形的面积之和为42,长方形PECF的面积为11,BE=DF=2,则长方形ABCD的面积为.
三、解答题
-
20. 计算:(1)、 +(2)、( )21.(1)、解方程组:(2)、因式分解:22. 小军解答:“化简 ” 的过程如图.试指出解答过程中错误步骤的序号,并写出正确的解答过程.
解:
= ………………………①
=2x-x+2 ………………………②
=x+2 ………………………③
23. 某校举办“数学计算能手大赛”.赛后将参赛学生的成绩按分数段分为五组,把大赛成绩 记为“优秀”,60 分记为“良好”, 分记为“一般”.绘制出以下不完整的统计图表:“数学计算能手大赛”成绩频数表
组别
成绩x(分,x为整数)
频数(人)
频率
一
2
0.04
二
10
0.2
三
14
b
四
a
0.32
五
8
0.16
“数学计算能手大赛”成绩扇形统计图

请根据上述信息,解答下列问题:
(1)、求出表中a,b的值;(2)、求本次大赛的优秀率;(3)、求扇形统计图中,“良好”部分所对应的圆心角 的度数.24. 已知:如图,∠1=∠C,∠E=∠B.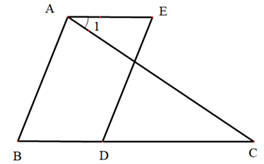 (1)、判断AB与DE的位置关系,并说明理由;(2)、若AB⊥AC于点A,∠1=36°,求∠BDE的度数.25. 某商场经销A,B两款商品,若买20件A商品和10件B商品用了360元;买30件A商品和5件B商品用了500元.(1)、求A、B两款商品的单价;(2)、若对A、B两款商品按相同折扣进行销售,某顾客发现用640元购买A商品的数量比用224元购买B商品的数量少20件,求对A、B两款商品进行了几折销售?(3)、若对A商品进行5折销售,B商品进行8折销售,某顾客同时购买A、B两种商品若干件,正好用完49.6元,问该顾客同时购买A、B两款商品各几件?
(1)、判断AB与DE的位置关系,并说明理由;(2)、若AB⊥AC于点A,∠1=36°,求∠BDE的度数.25. 某商场经销A,B两款商品,若买20件A商品和10件B商品用了360元;买30件A商品和5件B商品用了500元.(1)、求A、B两款商品的单价;(2)、若对A、B两款商品按相同折扣进行销售,某顾客发现用640元购买A商品的数量比用224元购买B商品的数量少20件,求对A、B两款商品进行了几折销售?(3)、若对A商品进行5折销售,B商品进行8折销售,某顾客同时购买A、B两种商品若干件,正好用完49.6元,问该顾客同时购买A、B两款商品各几件?