江苏省仪征市2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2020-08-24 类型：期末考试

进入出卷网下载

一、选择题

1. 下列计算正确的是（）

A、 $a^{2} + a^{4} = a^{6}$ B、 $2 a \cdot 4 a = 8 a$ C、 ${(a^{2})}^{3} = a^{6}$ D、 $a^{8} \div a^{2} = a^{4}$

查看试题解析
2. 甲型H1N1流感病毒的直径大约是0.000000081米，用科学记数法可表示为（）

A、8.1×10^﹣⁹米 B、8.1×10^﹣⁸米 C、81×10^﹣⁹米 D、0.81×10^﹣⁷米

查看试题解析
3. 如图，在△ABC中，BC＝5，∠A＝80°，∠B＝70°，把△ABC沿RS的方向平移到△DEF的位置，若CF＝4，则下列结论中错误的是（）

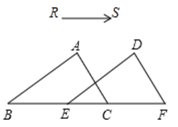A、BE＝4 B、∠F＝30° C、AB∥DE D、DF＝5

查看试题解析
4. 如图，将三角尺的直角顶点放在直尺的一边上，∠1＝30°，∠3＝20°，则∠2 的度数等于（）

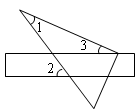A、50° B、30° C、20° D、15°

查看试题解析
5. 以下命题：（1）如果 a＜0， b＞0 ，那么 a + b＜0；（2）相等的角是对顶角；（3）同角的补角相等；（4）如果两条直线被第三条直线所截，那么同位角相等.其中真命题的个数是（）

A、0 B、1 C、2 D、3

查看试题解析
6. 如图，四边形ABCD中，∠A+∠B=200°，∠ADC、∠DCB的平分线相交于点O，则∠COD的度数是（）

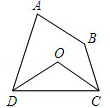A、80° B、90° C、100° D、110°

查看试题解析
7. 为了丰富学生课外小组活动，培养学生动手操作能力，王老师让学生把 6m 长的彩绳截成 2m 或 1m 的彩绳，用来做手工编织，在不造成浪费的前提下，你有几种不同的截法（）

A、2 种 B、3 种 C、4 种 D、5 种

查看试题解析
8. 已知 M = a² - a ， N = a -1（ a 为任意实数），则 M 、 N 的大小关系为（）

A、M＞ N B、M≥N C、M＜ N D、M≤ N

查看试题解析

二、填空题

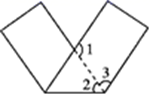
9. 计算：2a（-3b）=.

查看试题解析
10. 用不等式表示“x 与 5 的差不大于 1”：.

查看试题解析
11. 若一个多边形的每一个外角都等于40°，则这个多边形的边数是．

查看试题解析
12. 命题“等边三角形的三个内角相等”的逆命题是.

查看试题解析
13. 若 $a + b = \frac{1}{3}, a - b = - 3$ ，则 $a^{2} - b^{2}$ =.

查看试题解析
14. 计算： ${0.25}^{2019} \times 4^{2020}$ ＝.

查看试题解析
15. 已知（m-n）²=8，(m+n)²=2，则m²+n²=.

查看试题解析
16. 将一张长方形纸条折成如图所示的形状，若∠1=110°，则∠2=°.

查看试题解析
17. 若不等式组 ${\begin{array}{l} x > a \\ x \leq 2 \end{array}$ 无解，则 a 的取值范围是.

查看试题解析
18. 如图，在 $△$ ABC 中，AD、CE 是中线，若四边形 BDFE 的面积是 6，则 $△$ ABC 的面积为.

查看试题解析

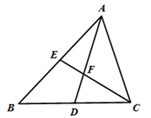
三、解答题

19. 计算：

(1)、 ${(- \frac{1}{2})}^{- 1} + {(- 2)}^{0} + | - 2 | - (- 3)$

(2)、 $(x + y) (x - y) - x (x + y) + 2 x y$

查看试题解析
20. 分解因式：

(1)、 $2 x^{2} - 4 x + 2$

(2)、 $a^{2} (x - y) + 9 b^{2} (y - x)$

查看试题解析
21. 解方程组或不等式组：

(1)、 ${\begin{array}{l} 2 x + y = 5 \\ x - 3 y = 6 \end{array}$

(2)、 ${\begin{matrix} x - 1 < 0 \\ 2 (x - 1) ⩽ 3 x \end{matrix}$

查看试题解析
22. 如图，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上.将△ABC向左平移2格，再向上平移4格.

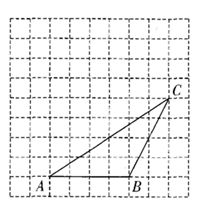(1)、请在图中画出平移后的△A′B′C′；

(2)、连接A A′、C C′，四边形AC C′A′的面积为；

(3)、在右图中能使S_△_ABC＝S_△_PBC的格点P的个数有个（点P异于点A）.

查看试题解析
23. 如图，CD是△ABC的角平分线，点E是AC边上的一点， $∠ E C D = ∠ E D C$ .

(1)、求证： $E D / / B C$ ；

(2)、 $∠ A = 30^{°}$ ， $∠ B D C = 65^{°}$ ，求∠DEC的度数.

查看试题解析
24. 若 $x + y = 2$ ，且 $(x + 3) (y + 3) = 12$ .

(1)、求xy的值；

(2)、求 $x^{2} + 3 x y + y^{2}$ 的值.

查看试题解析
25. 已知关于x、y的方程组 ${\begin{array}{l} x - y = - a - 1 \\ 2 x - y = - 3 a \end{array}$

(1)、求该方程组的解（用含a的代数式表示）；

(2)、若方程组的解满足 x＜0 ， y＞0 ，求 a 的取值范围.

查看试题解析
26. 某小区为了绿化环境，计划分两次购进 A、B 两种花草，第一次分别购进 A、B 两种花草40棵和30棵，共花费950元；第二次分别购进A、B两种花草30棵和20棵，共花费700元（两次购进的 A、B 两种花草价格均分别相同）.

(1)、A、B两种花草每棵的价格分别是多少元？

(2)、若购买A、B 两种花草共120棵（A、B 两种花草价格不变），且A种花草的数量不少于B种花草的数量的3倍，请你给出一种费用最省钱的方案，并求出该方案所需的费用.

查看试题解析
27. 阅读理解：已知 $m^{2} - 2 m n + 2 n^{2} - 8 n + 16 = 0$ ，求m 、n的值.
解：∵ $m^{2} - 2 mn + 2 n^{2} - 8 n + 16 = 0$

∴ $(m^{2} - 2 m n + n^{2}) + (n^{2} - 8 n + 16) = 0$

∴ ${(m - n)}^{2} + {(n - 4)}^{2} = 0$

∴ ${(m - n)}^{2} = 0 ， {(n - 4)}^{2} = 0$

∴ $n = 4 ， m = 4$ .

方法应用：

(1)、已知 $a^{2} + b^{2} - 10 a + 4 b + 29 = 0$ ，求a 、b 的值；

(2)、已知 $x + 4 y = 4$ .
①用含 y 的式子表示 x ：；

②若 $x y - z^{2} - 6 z = 10$ ，求 $y^{x + z}$ 的值.

查看试题解析
28. 已知 $△$ ABC，P 是平面内任意一点（A、B、C、P 中任意三点都不在同一直线上）.连接 PB、PC，设∠PBA＝s°，∠PCA＝t°，∠BPC＝x°，∠BAC＝y°.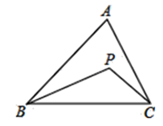

(1)、如图，当点 P 在 $△$ ABC 内时，
①若 y＝70，s＝10，t＝20，则 x＝；

②探究 s、t、x、y 之间的数量关系，并证明你得到的结论.

(2)、当点 P 在 $△$ ABC 外时，直接写出 s、t、x、y 之间所有可能的数量关系，并画出相应的图形.

查看试题解析