江苏省扬州市江都区2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2020-08-24 类型：期末考试

进入出卷网下载

一、选择题

1. 下列计算正确的是（）

A、 $a^{3} + a^{2} = a^{5}$ B、 $a^{3} \cdot a^{2} = a^{5}$ C、 ${(2 a^{2})}^{3} = 6 a^{6}$ D、 $a^{6} \div a^{2} = a^{3}$

查看试题解析
2. 如果a<b，下列各式中正确的是（）

A、ac²<bc² B、 $\frac{1}{a} > \frac{1}{b}$ C、 $\frac{a}{4} > \frac{b}{4}$ D、-3a>-3b

查看试题解析
3. 不等式组 ${\begin{array}{l} 2 x > - 4 \\ 3 x - 5 \leq 7 \end{array}$ 的解集在数轴上可以表示为（）

A、 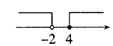B、 C、 D、

查看试题解析
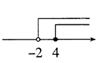4. 已知 ${\begin{matrix} x = 2 \\ y = - 1 \end{matrix}$ 是二元一次方程 $2 x + m y = 1$ 的一个解，则 $m$ 的值为（）

A、3 B、－5 C、－3 D、5

查看试题解析
5. 下列关于命题“若 $a^{2} > b^{2}$ ，则 $a > b$ ”的说法，正确的是（）

A、是真命题 B、是假命题，反例是“ $a = 1, b = 2$ ” C、是假命题，反例是“ $a = - 2, b = 1$ ” D、是假命题，反例是“ $a = - 1, b = - 2$ ”

查看试题解析
6. 若 $(x + 2 y) (2 x - m y - 1)$ 的结果中不含 $x y$ 项，则m的值为（）

A、4 B、-4 C、2 D、-2

查看试题解析
7. 如图，将长方形纸片ABCD进行折叠，如果∠BHG＝82°，那么∠BHE的度数为（）

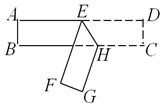A、49° B、50° C、51° D、59°

查看试题解析
8. 已知 $x = 4$ 是关于x的方程 $k x + b = 0 (k \neq 0 ， b > 0)$ 的解，则关于x的不等式 $k (x - 3) + 2 b > 0$ 的解集是（）

A、 $x > 11$ B、 $x < 11$ C、 $x > 7$ D、 $x < 7$

查看试题解析
9. 新型冠状病毒的形状一般为球形，直径大约为 $0.000000112 m$ ，将数据0.000000112用科学记数法表示为.

查看试题解析

二、填空题

10. 若 $a^{x} = 3, a^{y} = 2$ ，则 $a^{3 x - 2 y}$ 的值为.

查看试题解析
11. 若 $m - n = 3 ， m n = - 1$ ，则 ${(m + n)}^{2}$ ＝.

查看试题解析
12. 直角三角形两锐角互余的逆命题是.

查看试题解析
13. 内角和等于外角和2倍的多边形是边形.

查看试题解析
14. 将一副三角板如图放置，则图中的∠1＝°.

查看试题解析
15. △ABC的两条边的长度分别为3和5，若第三条边为偶数，则△ABC的周长为.

查看试题解析
16. 程大位，明代商人，珠算发明家，被称为珠算之父、卷尺之父. 少年时，读书极为广博，对数学颇感兴趣，60岁时完成其杰作《直指算法统宗》（简称《算法统宗》）. 在《算法统宗》里记载了一道趣题：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完.试问大、小和尚各多少人？如果设大和尚有x人，小和尚有y人，那么根据题意可列方程组为.

查看试题解析
17. 已知关于x，y的方程组 ${\begin{array}{l} x - 2 y = m \\ 2 x + 3 y = 2 m + 4 \end{array}$ 的解满足不等式组 ${\begin{array}{l} 3 x + y \leq 0 \\ x + 5 y > 0 \end{array}$ ，则满足条件的m的整数值为.

查看试题解析
18. 对于任意实数p、q，定义一种运算 $p ※ q = p - q + p q - 2$ ，等式的右边是通常的加减和乘法运算，例如： $4 ※ 5 = 4 - 5 + 4 \times 5 - 2 = 17$ .请根据上述定义解决问题：若关于 $x$ 的不等式组 ${\begin{array}{l} 2 ※ x < 4 ， \\ x ※ 3 \geq 2 m \end{array}$ 有5个整数解，则m的取值范围是.

查看试题解析

三、解答题

19. 计算：

(1)、 ${(- 1)}^{2} + {(- 2021)}^{0} + {(- \frac{1}{2})}^{- 2}$ ；

(2)、 ${(- 2 a^{2})}^{3} \cdot a^{2} + 4 a^{9} \div a$ .

查看试题解析
20. 因式分解：

(1)、 $6 x y - x^{2} - 9 y^{2}$ ；

(2)、 $a^{4} - 2 a {}^{2}b^{2} + b^{4}$ .

查看试题解析
21. 解方程组或不等式组：

(1)、 ${\begin{array}{l} 2 x + y = 4, \\ 3 x - 2 y = - 1 \end{array}$ ；

(2)、 ${\begin{array}{l} 5 x + 4 \geq 2 (x - 1), \\ \frac{2 x + 5}{3} - \frac{3 x - 2}{2} > 1 \end{array}$ .

查看试题解析
22. 如图，方格纸中每个小正方形的边长均为1，△ABC的三个顶点都在小正方形的顶点（小正方形的顶点叫格点）上.

(1)、利用格点在图中画出△ABC中AB边上的高CD；

(2)、①画出将△ABC先向右平移3格，再向下平移2格得到的△A₁B₁C₁；
②线段 $B B_{1}$ 与 $C C_{1}$ 的数量关系与位置关系是 ▲ ；

③在平移的过程中，线段AB扫过的部分所组成的封闭图形的面积为 ▲ .

查看试题解析
23. 先化简，再求值： ${(x - 3)}^{2} + 2 (x - 2) (x + 7) - (x + 2) (x - 2)$ ，其中 $x^{2} + 2 x - 4 = 0$ .

查看试题解析
24. 如图，已知AF分别与BD、CE交于点G、H，∠1＝50°，∠2＝130°.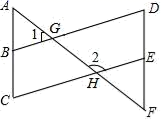

(1)、求证：BD∥CE；

(2)、若∠A＝∠F，探索∠C与∠D的数量关系，并证明你的结论.

查看试题解析
25. 若关于 $x, y$ 二元一次方程组 ${\begin{array}{l} x + y = 2 a + 1, \\ x - 2 y = - a - 5 \end{array}$ 的解 $x, y$ 的值大于0.

(1)、求a的取值范围；

(2)、若 $x, y$ 的值恰好是一个等腰三角形的腰和底边的长，且这个等腰三角形的周长为9，求 $a$ 的值.

查看试题解析
26.

(1)、用等号或不等号填空：比较 $4 x$ 与 $4 x^{2} + 2$ 的大小：
当 $x$ ＝ $1$ 时， $4 x$ $4 x^{2} + 2$ ；

当 $x = 0$ 时， $4 x$ $4 x^{2} + 2$ ；

当 $x$ ＝ $- 2$ 时， $4 x$ $4 x^{2} + 2$ ；

试猜想：无论x取何值， $4 x$ $4 x^{2} + 2$ ，请说明理由；

(2)、已知 $4 x^{2} + 2 y^{2} + 8 y + 16 = 4 x y$ ，求 $y^{x}$ 的值.

查看试题解析
27. 某制纸厂生产A型、B型两种不同规格的纸，需用甲、乙两种不同的原料.若甲原料成本为0.5元/m³ ，乙原料成本为1元/kg，其它相关数据如下表所示：

甲原料/m³

乙原料/kg

售价/元

每百张A型纸

1

2

4

每百张B型纸

1.2

3

5

(1)、若生产这两种纸需用甲原料108m³、乙原料240kg，则这两种规格的纸各多少百张？

(2)、若该厂生产A型纸a百张，则生产这种A型纸的利润是多少元（用含a 的代数式表示）？（利润＝售价－成本）

(3)、该厂发现，当制纸总量超过10000百张时，需额外支出8800元的设备维护费，现该厂接到一笔订单，要求生产A型纸的数量是B型纸数量的2倍，若该厂希望获得13200元的利润，则有哪几种生产方案？

查看试题解析
28. 如图1，△ABC中，∠ABC＝∠BAC，D是BC延长线上一动点，连接AD，AE平分∠CAD交CD于点E，过点E作EH⊥AB，垂足为点H.直线EH与直线AC相交于点F.设∠AEH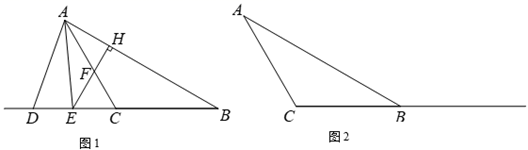＝ $α$ ，∠ADC＝ $β$ .

(1)、求证：∠EFC＝∠FEC；

(2)、①若∠B＝30°，∠CAD＝50°，则 $α$ ＝， $β$ ＝；
②试探究 $α$ 与 $β$ 的关系，并说明理由；

(3)、若将“D是BC延长线上一动点”改为“D是CB延长线上一动点”，其它条件不变，请在图2中补全图形，并直接写出 $α$ 与 $β$ 的关系.

查看试题解析

	甲原料/m³	乙原料/kg	售价/元
每百张A型纸	1	2	4
每百张B型纸	1.2	3	5