江苏省泰州市姜堰区2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2020-08-24 类型：期末考试

进入出卷网下载

一、选择题

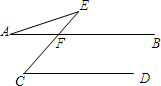
1. 下列说法正确的是（）

A、 $2 a \cdot 3 a = 6 a$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、 ${(- a^{3})}^{2} = a^{6}$ D、 $a^{6} \div a^{2} = a^{3}$

查看试题解析
2. 不等式 $2 x + 3 \geq 1$ 的解集是（）

A、 $x \leq - 1$ B、 $x \geq - 1$ C、 $x \leq - 2$ D、 $x \geq - 2$

查看试题解析
3. 如图，AB∥CD，CE交AB于点F.∠A＝20°，∠E＝30°，则∠C的度数为（　　）

A、50° B、55° C、60° D、65°

查看试题解析
4. 如图，从边长为a的大正方形中剪掉一个边长为b的小正方形，将图1中的阴影部分沿虚线剪开，拼成图2的长方形，根据图形的变化过程写出一个正确的等式是（）

A、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ B、 ${(a - b)}^{2} = a^{2} - b^{2}$ C、 ${(a - b)}^{2} = a^{2} - b^{2}$ D、 $a^{2} - b^{2} = (a + b) (a - b)$

查看试题解析
5. 下列四个命题中，真命题有（）
①两条直线被第三条直线所截，内错角相等；②如果 $∠ 1$ 和 $∠ 2$ 是对顶角，那么 $∠ 1 = ∠ 2$ ；③如果a<0、b<0，那么a+b<0；④平方等于4的数是2.

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 疫情期间，小明要用16元钱买A、B两种型号的口罩，两种型号的口罩必须都买，16元全部用完.若A型口罩每个3元，B型每个2元，则小明的购买方案有（）

A、2种 B、3种 C、4种 D、5种

查看试题解析

二、填空题

7. 计算： $2 a^{2} b \cdot 3 a b^{2}$ =.

查看试题解析
8. 将0.0012用科学记数法表示为.

查看试题解析
9. “x的3倍与2的差是正数”用不等式表示为.

查看试题解析
10. 已知 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ 是方程2x﹣y+k＝0的解，则k的值是.

查看试题解析
11. 一个三角形的两边分别是2和3，若它的第三边为奇数，则第三边为.

查看试题解析
12. 已知一个多边形的内角和是720°，则这个多边形是边形.

查看试题解析
13. 若 $(x + 3) (x - m) = x^{2} + x + n$ ，则 $m n =$ .

查看试题解析
14. 已知二元一次方程 $x + 2 y = - 5$ ，当 $x > - 1$ 时，y的取值范围是.

查看试题解析
15. 已知 $9^{m} \times 27^{n} = 81$ ，则 $6 - 4 m - 6 n$ 的值为.

查看试题解析
16. 如图，在△ABC中，∠ACB=60°，∠ABC= $α$ （20°< $α$ <120°），AE平分△ABC的外角∠BAD，CF将∠ACB分成1：2两部分.若AE、CF交于点G，则∠AGC的度数为（用含 $α$ 的代数式表示）.

查看试题解析

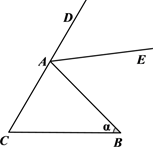
三、解答题

17. 计算：

(1)、 ${(-1)}^{2020} + {(π -3 .14)}^{0} + {(\frac{1}{2})}^{- 2}$ ；

(2)、 $a^{2} \cdot a^{4} + {(2 a^{3})}^{2}$ .

查看试题解析
18. 因式分解：

(1)、 $4 a^{2} - 9$ ；

(2)、 $2 x^{2} y - 8 x y + 8 y$ .

查看试题解析
19. 解下列方程组或不等式组：

(1)、 ${\begin{array}{l} 2 x - y = 1 \\ x + 3 y = 11 \end{array}$ ；

(2)、 ${\begin{array}{l} 1 - 2 x > 0 \\ \frac{x + 2}{2} - \frac{x}{3} \geq 1 \end{array}$ .

查看试题解析
20. 先化简，再求值： ${(x -2)}^{2} - 4 x (x - 1) + (2 x + 1) (2 x - 1)$ ，其中 $x = 2$ .

查看试题解析
21. 在等式 $y = a x + b$ 中，当 $x = 5$ 时， $y = 6$ ；当 $x = - 3$ 时， $y = - 10$ .

(1)、求a、b的值；

(2)、当 $x = 1$ 时，求y的值.

查看试题解析
22. 如图，在△ABC中，D为AC边上一点，∠A=∠ABD，∠C=∠CBD.

(1)、求∠ABC的度数；

(2)、若DE平分∠ADB交AB于点E，求证：DE∥BC.

查看试题解析
23. 如图

(1)、已知：如图，直线AB、CD、EF被直线BF所截， $∠ B + ∠ 1 = 180 °$ ， $∠ 2 = ∠ 3$ .求证： $∠ B + ∠ F = 180 °$ ；

(2)、你在（1）的证明过程中应用了哪两个互逆的真命题.

查看试题解析

24. 某物流公司安排A、B两种型号的卡车向灾区运送抗灾物资，装运情况如下：

装运批次	卡车数量		装运物资重量
装运批次	A种型号	B种型号	装运物资重量
第一批	2辆	4辆	56吨
第二批	4辆	6辆	96吨

(1)、求A、B两种型号的卡车平均每辆装运物资多少吨；

(2)、该公司计划安排A、B两种型号的卡车共15辆装运150吨抗灾物资，那么至少要安排多少辆A种型号的卡车.

查看试题解析

25. 阅读理解：
定义：若一元一次方程的解在一元一次不等式组解集范围内，则称该一元一次方程为该不等式组的“子方程”.例如： $2 x - 1 = 3$ 的解为 $x = 2$ ， ${\begin{array}{l} 2 x - 3 < 9 - x \\ 5 x + 5 \geq 2 x - 4 \end{array}$ 的解集为 $- 3 \leq x < 4$ ，不难发现 $x = 2$ 在 $- 3 \leq x < 4$ 的范围内，所以 $2 x - 1 = 3$ 是 ${\begin{array}{l} 2 x - 3 < 9 - x \\ 5 x + 5 \geq 2 x - 4 \end{array}$ 的“子方程”.

问题解决：

(1)、在方程① $3 x - 1 = 0$ ，② $\frac{2}{3} x - 1 = 0$ ，③ $2 x + 3 (x + 2) = 21$ 中，不等式组 ${\begin{array}{l} 2 x - 1 > x + 1 \\ 3 (x - 2) - x \leq 4 \end{array}$ 的“子方程”是；（填序号）

(2)、若关于x的方程 $2 x - k = 2$ 是不等式组 ${\begin{array}{l} 3 x - 6 > 4 - x \\ x - 1 \geq 4 x - 10 \end{array}$ 的“子方程”，求k的取值范围；

(3)、若方程 $2 x + 4 = 0$ ， $\frac{2 x - 1}{3} = - 1$ 都是关于x的不等式组 ${\begin{array}{l} (m - 2) x < m - 2 \\ x + 5 \geq m \end{array}$ 的“子方程”，直接写出m的取值范围.

查看试题解析
26. 用周长相等的正方形ABCD和长方形AEFG，按如图所示的方式叠放在一起（其中点E在AB上，点G在AD延长线上，EF和DC交于点H），正方形ABCD的边长为m，长方形AEFG长为x，宽为y（y<m<x）.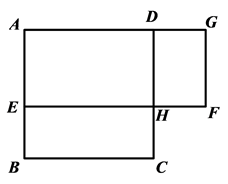

(1)、写出x、y 、m之间的等量关系；

(2)、求证：HC=HF；

(3)、若四边形DHFG为正方形，求x、y（用含有m的代数式表示）；

(4)、比较四边形BEHC与四边形DHFG面积的大小，并说明理由.

查看试题解析