江苏省南京市联合体2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2020-08-24 类型：期末考试

进入出卷网下载

一、选择题

1. 计算a⁶÷a²的结果是（）

A、a² B、a³ C、a⁴ D、a⁶

查看试题解析
2. 某红外线遥控器发出的红外线波长为0.00 000 09米，用科学记数法表示这个数是（）

A、 $9 \times 10^{- 7}$ B、 $9 \times 10^{- 8}$ C、 $0.9 \times 10^{- 7}$ D、 $0.9 \times 10^{- 8}$

查看试题解析
3. 已知a＞b，则下列不等关系中正确的是（）

A、ac＞bc B、a＋c＞b＋c C、a－1＞b＋1 D、ac²＞bc²

查看试题解析
4. 如图，直线a∥b，点B在直线b上，且AB⊥BC，∠1＝40°，那么∠2的度数是（）

A、35° B、45° C、50° D、65°

查看试题解析
5. 如图，已知CB∥DF，则下列结论成立的是（）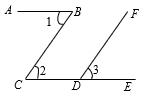

A、∠1＝∠2 B、∠2＝∠3 C、∠1＝∠3 D、∠1＋∠2＝180º

查看试题解析
6. 下列命题是真命题的是（）

A、如果a²=b² ，那么a=b B、如果两个角是同位角，那么这两个角相等 C、相等的两个角是对项角 D、在同一平面内，垂直于同一条直线的两条直线平行

查看试题解析
7. 《九章算术》中记载：“今有上禾三秉，益实六斗，当下禾十秉；下禾五秉，益实一斗，当上禾二秉. 问上、下禾实一秉各几何？”其大意是：今有上等稻子三捆，若打出来的谷子再加六斗，则相当于十捆下等稻子打出来的谷子；有下等稻子五捆，若打出来的谷子再加一斗，则相当于两捆上等稻子打岀来的谷子. 问上等、下等稻子每捆打多少斗谷子？设上等稻子每捆打x斗谷子，下等稻子每捆打y斗谷子，根据题意可列方程组为（）

A、 ${\begin{array}{l} 3 x + 6 = 10 x \\ 5 x + 1 = 2 y \end{array}$ B、 ${\begin{array}{l} 3 x - 6 = 10 y \\ 5 y - 1 = 2 x \end{array}$ C、 ${\begin{array}{l} 3 x + 6 = 10 y \\ 5 x + 1 = 2 x \end{array}$ D、 ${\begin{array}{l} 3 y - 6 = 10 x \\ 5 x - 1 = 2 y \end{array}$

查看试题解析
8. 关于x的不等式x－a≥1.若x＝1是不等式的解，x＝－1不是不等式的解，则a的范围为（）

A、－2≤a≤0 B、－2＜a＜0 C、－2≤a＜0 D、－2＜a≤0

查看试题解析

二、填空题

9. 计算：2⁰＝，（ $\frac{1}{2}$ ）^－³＝.

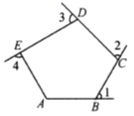
查看试题解析
10. 若三角形有两边长分别为2和5，第三边为a，则a的取值范围是.

查看试题解析
11. 写出命题“两直线平行,同旁内角互补.”的逆命题。

查看试题解析
12. 分解因式：a³－a=

查看试题解析
13. 已知 ${\begin{matrix} x = 1 \\ y = - 2 \end{matrix}$ 是方程2x﹣ay=3的一个解，则a的值是．

查看试题解析
14. 如图， $∠ 1$ 、 $∠ 2$ 、 $∠ 3$ 、 $∠ 4$ 是五边形 $A B C D E$ 的4个外角，若 $∠ A = 120 °$ ，则 $∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 =$ °．

查看试题解析
15. 已知2^a＝3，4^b＝5，则 $2^{a}^{+ 2 b}$ 的值是.

查看试题解析
16. 若a-b=3，ab=1，则a²+b²=.

查看试题解析
17. 已知不等式组 ${\begin{array}{l} x < 1 \\ x > n \end{array}$ 有3个整数解，则n的取值范围是.

查看试题解析
18. 如图，C是线段AB上一点，∠DAC＝∠D，∠EBC＝∠E，AO平分∠DAC，BO平分∠EBC.若∠DCE＝40°，则∠O＝°.

查看试题解析

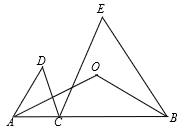
三、解答题

19. 计算

(1)、（－t）⁵÷（－t）³·（－t）²；

(2)、（2a－b）（a－2b）.

查看试题解析
20. 分解因式

(1)、 $m^{3} - 4 m^{2} + 4 m$ ；

(2)、 $a (a - 1) + a - 1$ .

查看试题解析
21. 先化简，再求值：（2a－b）²－（2a－3b）（2a＋3b），其中，a＝ $\frac{1}{2}$ ，b＝1.

查看试题解析
22. 解方程组 ${\begin{matrix} x + 3 y = - 1 \\ 3 x - 2 y = 8 \end{matrix}$ ．

查看试题解析
23.

(1)、解不等式 $\frac{3 x + 1}{2}$ － $\frac{5 x - 1}{4}$ ≤1，并把解集在数轴上表示出来.

(2)、解不等式组 ${\begin{array}{l} 3 - x > 0 \\ \frac{5 x + 1}{2} + 1 \geq x \end{array}$ 并写出它的所有整数解.

查看试题解析
24. 如图，在△ABC中，BE是AC边上的高，DE∥BC，∠ADE＝48°，∠C＝62°，求∠ABE的度数.

查看试题解析
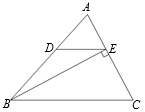25. 如图，已知AB∥CD，AE平分∠BAD，DF平分∠ADC，EF交AD于点O，求证∠E＝∠F.

查看试题解析
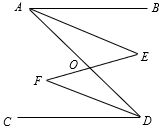26. 新冠肺炎疫情期间，某口罩厂为生产更多的口罩满足疫情防控需求，决定拨款456万元购进A，B两种型号的口罩机共30台.两种型号口罩机的单价和工作效率分别如下表：

单价/万元

工作效率/（只/h）

A种型号

16

4000

B种型号

14.8

3000

(1)、求购进A，B两种型号的口罩生产线各多少台.

(2)、现有200万只口罩的生产任务，计划安排新购进的口罩机共15台同时进行生产.若工厂的工人每天工作8h，则至少租用A种型号的口罩机多少台才能在5天内完成任务？

查看试题解析
27. （概念认识）
如图①，在∠ABC中，若∠ABD＝∠DBE＝∠EBC，则BD，BE叫做∠ABC的“三分线”.其中，BD是“邻AB三分线”，BE是“邻BC三分线”.

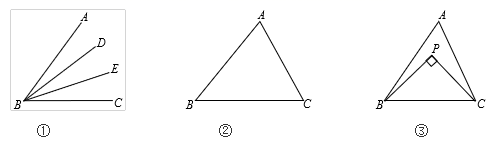(1)、（问题解决）如图②，在△ABC中，∠A＝70°，∠B＝45°，若∠B的三分线BD交AC于点D，则∠BDC＝°；

(2)、如图③，在△ABC中，BP、CP分别是∠ABC邻AB三分线和∠ACB邻AC三分线，且BP⊥CP，求∠A的度数；

(3)、（延伸推广）在△ABC中，∠ACD是△ABC的外角，∠B的三分线所在的直线与∠ACD的三分线所在的直线交于点P.若∠A＝m°，∠B＝n°，直接写出∠BPC的度数.（用含 m、n的代数式表示）

查看试题解析

	单价/万元	工作效率/（只/h）
A种型号	16	4000
B种型号	14.8	3000