江苏省溧阳市2019-2020学年七年级下学期数学期末考试试卷
试卷更新日期:2020-08-24 类型:期末考试
一、选择题
-
1. 下列各式从左到右的变形,因式分解正确的是( )A、 B、 C、 D、2. 如图,若l1∥l2 , l3∥l4 , 则图中与∠1互补的角有( )
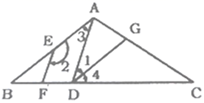
 A、1个 B、2个 C、3个 D、4个3. 不等式 的最大整数解是( )A、0 B、1 C、 D、24. 如图,在△ABC中,∠C=90°,点D在BC上,DE⊥AB,垂足为E,则△ABD的BD边上的高是( )
A、1个 B、2个 C、3个 D、4个3. 不等式 的最大整数解是( )A、0 B、1 C、 D、24. 如图,在△ABC中,∠C=90°,点D在BC上,DE⊥AB,垂足为E,则△ABD的BD边上的高是( )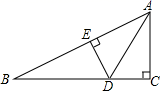 A、AD B、DE C、AC D、BC5. 如图,方格中的点A,B,C,D,E称为“格点”(格线的交点),以这5个格点中的3点为顶点画三角形,可以画等腰三角形和直角三角形的个数分别是( )
A、AD B、DE C、AC D、BC5. 如图,方格中的点A,B,C,D,E称为“格点”(格线的交点),以这5个格点中的3点为顶点画三角形,可以画等腰三角形和直角三角形的个数分别是( )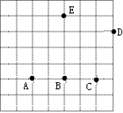 A、2和3 B、3和3 C、2和4 D、3和46. 下列四个命题:①两直线平行,内错角相等;②若a>0,则a+3>0;③两个角相等,它们一定是对顶角;④二元一次方程 的解为 其中为真命题的个数是( )A、1 B、2 C、3 D、47. 已知关于x、y的方程组 的解是 ,则a、b的值是( )A、 B、 C、 D、8. 如图,在△ABC中,∠CAB=65°,现将△ABC绕着点A逆时针旋转一定角度 ,并且使 ,那么旋转角的度数a为( )
A、2和3 B、3和3 C、2和4 D、3和46. 下列四个命题:①两直线平行,内错角相等;②若a>0,则a+3>0;③两个角相等,它们一定是对顶角;④二元一次方程 的解为 其中为真命题的个数是( )A、1 B、2 C、3 D、47. 已知关于x、y的方程组 的解是 ,则a、b的值是( )A、 B、 C、 D、8. 如图,在△ABC中,∠CAB=65°,现将△ABC绕着点A逆时针旋转一定角度 ,并且使 ,那么旋转角的度数a为( )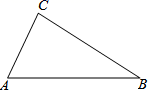 A、65° B、25° C、35° D、40°
A、65° B、25° C、35° D、40°二、填空题
-
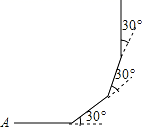
9. 六边形的内角和为°.10. =.11. 已知方程 ,请用含x的代数式表示y,y=.12. 一个长方体的高是10cm,它的底面是边长为4cm的正方形,如果底面正方形的边长增加acm,则它的体积增加了 .13. 水滴不断地滴在一块石头上,经过100年,石头上形成了一个深为6×10-2m的小洞,用科学记数法表示平均每月小洞增加的深度m.14. 如图,小亮从A点出发,沿直线前进15米后向左转30°,再沿直线前进15米,又向左转30°,…照这样走下去,他第一次回到出发地A点时,一共走了米.
 15. 已知 ,则 =.16. 如图,现将一块含有30°角的直角三角板的顶点放在平行线的一条直线上,与另一条直线的夹角为∠2,若∠1=2∠2,那么∠1=°.
15. 已知 ,则 =.16. 如图,现将一块含有30°角的直角三角板的顶点放在平行线的一条直线上,与另一条直线的夹角为∠2,若∠1=2∠2,那么∠1=°.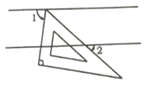 17. 如图,在直角三角形ABC中,点P、Q分别是AC、BC边上的两个动点,MP、NQ分别平分∠APQ和∠BQP,交AB于点M、N,MR、NR又分别平分∠BMP和∠ANQ,两条角平分线交于点R,则∠R=°.
17. 如图,在直角三角形ABC中,点P、Q分别是AC、BC边上的两个动点,MP、NQ分别平分∠APQ和∠BQP,交AB于点M、N,MR、NR又分别平分∠BMP和∠ANQ,两条角平分线交于点R,则∠R=°.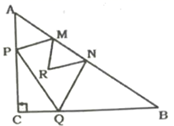 18. 一个三角形的3条边长分别为 , , ,它的周长不超过39cm,则x的取值范围.
18. 一个三角形的3条边长分别为 , , ,它的周长不超过39cm,则x的取值范围.三、解答题
-
19. 计算:(1)、(2)、(x-y+3)(x+y-3)(3)、(4)、20. 把下列代数式分解因式:(1)、(2)、21. 解下列方程组:(1)、(2)、22. 解下列不等式(组),并把解集在数轴上表示出来:(1)、(2)、23. 作图题:如图,在△ABC中,∠BAC是钝角.
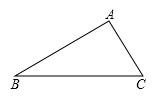 (1)、①画出边BC上的中线AD ;
(1)、①画出边BC上的中线AD ;②画出边BC上的高AH ;
(2)、在所画图形中,共有个三角形,其中面积一定相等的三角形是.24. 今年疫情期间,某生产医用产品企业,为了取得抗击疫情最后的胜利,决定购买甲、乙两种不同型号的生产机器加快防护服生产.据了解,甲、乙两种型号的机器单价分别3.1万元和4.6万元.(1)、若购买甲、乙两种型号的机器共50台,恰好支出200万元,求甲、乙两种型号的机器各购买了多少台?(2)、在(1)中条件下,如果甲种型号机器每天可以生产1500套防护服,乙种型号的机器每天可以生产2000套防护服,根据疫情需要,企业要求每天生产的防护服至少达到81000套,但是,厂里电力供应最多只允许45台机器同时运行,请问共有几种生产方案?并说明哪种方案生产防护服最多.