河南省新蔡县2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2020-08-24 类型：期末考试

进入出卷网下载

一、选择题

1. 在方程：3x－y＝2， $\frac{x}{2}$ ＋ $\frac{2}{x}$ ＝0， $\frac{x}{2}$ ＝1，3x²＝2x＋6中，一元一次方程的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 在下列条件中：①∠A+∠B=∠C，②∠A：∠B：∠C=1：2：3，③∠A=90°﹣∠B，④∠A=∠B=∠C中，能确定△ABC是直角三角形的条件有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 如图，在数轴上表示某不等式组中的两个不等式的解集，则该不等式组的解集为（）.

A、x＜4 B、x＜2 C、2＜x＜4 D、x＞2

查看试题解析
4. 三角形的两边长分别是4和7，则第三边长不可能是（）

A、4 B、6 C、10 D、12

查看试题解析
5. 已知关于x的不等式组 ${\begin{matrix} x \leq 2 \\ x > a \end{matrix}$ ，无解，则a的取值范围是（）

A、 $a$ ≤2 B、 $a$ ≥2 C、 $a$ ＜2 D、 $a$ ＞2

查看试题解析
6. 如图，将周长为10的△ABC沿BC方向平移1个单位得到△DEF，则四边形ABFD的周长为（　　）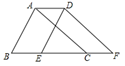

A、8 B、10 C、12 D、14

查看试题解析
7. 若a＜b＜0，则下列式子：①a＋1＜b＋2；② $\frac{a}{b} > 1$ ；③a＋b＜ab；④ $\frac{1}{a} < \frac{1}{b}$ 中，正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，△ABC以点C为旋转中心，旋转后得到△EDC，已知AB＝1.5，BC＝4，AC＝5，则DE＝（）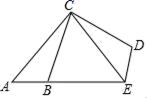

A、1.5 B、3 C、4 D、5

查看试题解析
9. 用正三角形和正六边形铺成一个平面，则在同一个顶点处，正三角形和正六边形的个数之比为（）

A、4:1 B、1:1 C、1:4 D、4:1或1:1

查看试题解析
10. 将一副三角板如图放置，使点A在DE上，BC∥DE，则∠AFC的度数是（　　）

A、45° B、50° C、60° D、75°

查看试题解析

二、填空题

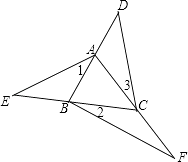
11. 将方程 $4 x + 2 y = 6$ 变形成用x的代数式表示y，则y=.

查看试题解析
12. 在实数范围内定义一种新运算“⊕”，其运算规则为：a⊕b=2a+3b.如：1⊕5=2×1+3×5=17.则不等式-x⊕4＜0的解集为

查看试题解析
13. 若关于x，y的二元一次方程组 ${\begin{array}{l} 2 x + y = 3 k - 1 \\ x + 2 y = - 2 \end{array}$ 的解满足 $x + y = 1$ ，则k的值是；

查看试题解析
14. 如图，D、E、F分别是△ABC三边延长线上的点，则∠D+∠E+∠F+∠1+∠2+∠3=度．

查看试题解析
15. 如图所示，△COD是△AOB绕点O顺时针方向旋转35°后所得的图形，点C恰好在AB上，∠AOD＝90°，则∠BOC的度数是.

查看试题解析

三、解答题

16. 按要求解方程（组）

(1)、 $\frac{x + 1}{3} + 1 = x - \frac{x - 1}{2}$

(2)、 ${\begin{array}{l} 3 x + 2 y = 5 ① \\ 2 x + 5 y = 7 ② \end{array}$

查看试题解析
17. 不等式（组）

(1)、解不等式： $\frac{2 x - 1}{3} ⩽ \frac{3 x + 2}{4} - 1$ ，并把解集表示在数轴上.

(2)、解不等式组： ${\begin{array}{l} \frac{x - 3}{2} + 3 ⩾ x + 1 ① \\ 1 - 3 (x - 1) < 8 - x ② \end{array}$ ，并写出整数解.

查看试题解析
18. 在图的正方形网格中有一个三角形OAB，请你在网格中分别按下列要求画出图形
①画出△OAB向左平移3个单位后的三角形；

②画出△OAB绕点O旋转180°后的三角形；

③画出△OAB沿y轴翻折后的图形.

查看试题解析
19. 已知，x=2是方程2﹣ $\frac{1}{3}$ （m﹣x）=2x的解，求代数式m²﹣（6m+2）的值．

查看试题解析
20. 已知 $y = k x + b$ ，当 $x = 1$ 时， $y = 3$ ；当 $x = - 2$ 时， $y = 9$ . 求出k，b的值；

查看试题解析
21. 某厂接到遵义市一所中学的冬季校服订做任务，计划用A、B两台大型设备进行加工.如果单独用A型设备需要90天做完，如果单独用B型设备需要60天做完，为了同学们能及时领到冬季校服，工厂决定由两台设备同时赶制.

(1)、两台设备同时加工，共需多少天才能完成？

(2)、若两台设备同时加工30天后，B型设备出了故障，暂时不能工作，此时离发冬季校服时间还有13天.如果由A型设备单独完成剩下的任务，会不会影响学校发校服的时间？请通过计算说明理由.

查看试题解析
22. 如图，在ΔABC中，已知∠ABC=60°，∠ACB=54°，BE是AC边上的高，CF是AB边上的高，H是BE和CF的交点，HD是∠BHC的平分线，求∠ABE、∠ACF和∠CHD的度数.

查看试题解析
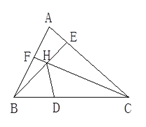23.

(1)、求A种鱼苗和B种鱼苗各多少箱？

(2)、现计划租用甲、乙两种货车共8辆，一次性将这批鱼苗全部运往同一目的地。已知甲种货车最多可装A种鱼苗40箱和B种鱼苗10箱，乙种货车最多可装A种鱼苗和B种鱼苗各20箱。如果甲种货车每辆需付运输费4000元，乙种货车每辆需付运输费3600元，则安排甲、乙两种货车有哪几种不同的方案？并说明选择哪种方案可使运输费最少？最少运输费是多少元？

查看试题解析