天津市南开区2019-2020学年九年级上学期数学第一次月考试卷
试卷更新日期:2020-08-24 类型:月考试卷
一、单选题
-
1. 下列方程中,是一元二次方程的是( )A、 B、 C、 D、2. 如图,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 某学习小组的6名同学在一次数学竞赛中的成绩分别是94分、98分、90分、94分、80分、74分,则下列结论正确的是( )A、中位数是90分 B、众数是94分 C、平均分是91分 D、方差是204. 如果a、b同号,那么二次函数y=ax2+bx+1的大致图象是( )A、
3. 某学习小组的6名同学在一次数学竞赛中的成绩分别是94分、98分、90分、94分、80分、74分,则下列结论正确的是( )A、中位数是90分 B、众数是94分 C、平均分是91分 D、方差是204. 如果a、b同号,那么二次函数y=ax2+bx+1的大致图象是( )A、 B、
B、 C、
C、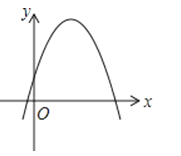 D、
D、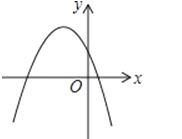 5. 已知二次函数 ,下列说法正确的是( )A、开口向上,顶点坐标 B、开口向下,顶点坐标 C、开口向上,顶点坐标 D、开口向下,顶点坐标6. 函数 的图象不经过第二象限,则 的取值范围是( )A、 B、 C、 D、7. 如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,则∠A的度数为( )
5. 已知二次函数 ,下列说法正确的是( )A、开口向上,顶点坐标 B、开口向下,顶点坐标 C、开口向上,顶点坐标 D、开口向下,顶点坐标6. 函数 的图象不经过第二象限,则 的取值范围是( )A、 B、 C、 D、7. 如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,则∠A的度数为( )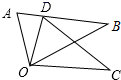 A、70° B、75° C、60° D、65°8. 受国际金融危机影响,市自来水公司号召全市市民节约用水.决定采取月用水量分段收费办法,某户居民应交水费y(元)与用水量x(吨)的函数关系如图所示.若该用户本月用水21吨,则应交水费( )
A、70° B、75° C、60° D、65°8. 受国际金融危机影响,市自来水公司号召全市市民节约用水.决定采取月用水量分段收费办法,某户居民应交水费y(元)与用水量x(吨)的函数关系如图所示.若该用户本月用水21吨,则应交水费( )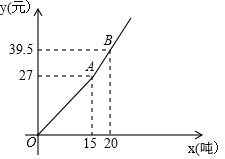 A、52.5元 B、45元 C、42元 D、37.8元9. 在函数y= (a为常数)的图象上有三个点(﹣1,y1),(﹣ ,y2),( ,y3),则函数值y1、y2、y3的大小关系是( )A、y2<y1<y3 B、y3<y2<y1 C、y1<y2<y3 D、y3<y1<y210. 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
A、52.5元 B、45元 C、42元 D、37.8元9. 在函数y= (a为常数)的图象上有三个点(﹣1,y1),(﹣ ,y2),( ,y3),则函数值y1、y2、y3的大小关系是( )A、y2<y1<y3 B、y3<y2<y1 C、y1<y2<y3 D、y3<y1<y210. 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )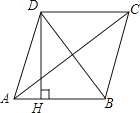 A、 B、 C、5 D、411. 直线y= x+4与x轴、y轴分别交于点A和点B , 点C , D分别为线段AB , OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( ).
A、 B、 C、5 D、411. 直线y= x+4与x轴、y轴分别交于点A和点B , 点C , D分别为线段AB , OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( ).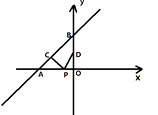 A、(-3,0) B、(-6,0) C、(- ,0) D、(- ,0)12. 如图,在正方形 中, ,点 , 分别在 、 上, , , 相交于点 ,若图中阴影部分的面积与正方形 的面积之比为 ,则 的周长为( )
A、(-3,0) B、(-6,0) C、(- ,0) D、(- ,0)12. 如图,在正方形 中, ,点 , 分别在 、 上, , , 相交于点 ,若图中阴影部分的面积与正方形 的面积之比为 ,则 的周长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 已知函数 ,当时,函数 随 增大而减小.14. 在一个不透明的盒子里装有4个黑球和若干个白球,它们除颜色外完全相同,摇匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复,共摸球40次,其中10次摸到黑球,则估计盒子中大约有个白球.15. 若x=0是关于x的一元二次方程(m+2)x2﹣3x+m2﹣4=0的一个根,则m的值为 .16. )如图,Rt△ABC中,C= 90o , 以斜边AB为边向外作正方形 ABDE,且正方形对角线交于点D,连接OC,已知AC=5,OC=6 ,则另一直角边BC的长为 .
 17. 如图,在矩形ABCD中,AD= AB , ∠BAD的平分线交BC于点E , DH⊥AE于点H , 连接BH并延长交CD于点F , 连接DE交BF于点O , 下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF , 其中正确的有 .
17. 如图,在矩形ABCD中,AD= AB , ∠BAD的平分线交BC于点E , DH⊥AE于点H , 连接BH并延长交CD于点F , 连接DE交BF于点O , 下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF , 其中正确的有 . 18. 如图,在每个小正方形边长为1的网格中,点A,B,C均在格点上.
18. 如图,在每个小正方形边长为1的网格中,点A,B,C均在格点上. (1)、AC的长度等于;(2)、在图中有一点P,若连接AP,PB,PC,满足AP平分∠A,且PC=PB,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明)
(1)、AC的长度等于;(2)、在图中有一点P,若连接AP,PB,PC,满足AP平分∠A,且PC=PB,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明)三、解答题
-
19. 解下列方程:(1)、x2﹣4x﹣1=0(配方法)(2)、(x+4)2=5(x+4)20. 箱子里有4瓶牛奶,其中有一瓶是过期的.现从这4瓶牛奶中不放回地任意抽取2瓶.(1)、请用树状图或列表法把上述所有等可能的结果表示出来;(2)、求抽出的2瓶牛奶中恰好抽到过期牛奶的概率.21. 如图,一次函数的图象与反比例函数的图象交于A(﹣3,1)、B(m,3)两点,
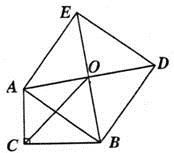
 (1)、求反比例函数和一次函数的解析式;(2)、写出使一次函数的值大于反比例函数的x的取值范围;(3)、连接AO、BO,求△ABO的面积.22. 如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF,请回答下列问题:
(1)、求反比例函数和一次函数的解析式;(2)、写出使一次函数的值大于反比例函数的x的取值范围;(3)、连接AO、BO,求△ABO的面积.22. 如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF,请回答下列问题: (1)、四边形ADEF是什么四边形?(2)、当△ABC满足什么条件时,四边形ADEF是矩形?(3)、当△ABC满足什么条件时,以A、D、E、F为顶点的四边形不存在?23. 某房地产开发公司计划建A、B两种户型的经济适用住房共80套,该公司所筹资金不少于2090万元,但不超过2096元,且所筹资金全部用于建房,两种户型的建房成本和售价如下表:(1)、该公司对这两种户型住房有哪几种建房方案?(2)、若该公司所建的两种户型住房可全部售出,利用函数的知识说明采取哪一种建房方案获得利润最大?并求出最大利润.
(1)、四边形ADEF是什么四边形?(2)、当△ABC满足什么条件时,四边形ADEF是矩形?(3)、当△ABC满足什么条件时,以A、D、E、F为顶点的四边形不存在?23. 某房地产开发公司计划建A、B两种户型的经济适用住房共80套,该公司所筹资金不少于2090万元,但不超过2096元,且所筹资金全部用于建房,两种户型的建房成本和售价如下表:(1)、该公司对这两种户型住房有哪几种建房方案?(2)、若该公司所建的两种户型住房可全部售出,利用函数的知识说明采取哪一种建房方案获得利润最大?并求出最大利润.A
B
成本(万元/套)
25
28
售价(万元/套)
30
34
24. 已知:如图1,在平面直角坐标系中,直线1:y=﹣x+4与坐标轴分别相交于点A、B与l2:y= x相交于点C . (1)、求点C的坐标;(2)、若平行于y轴的直线x=a交于直线1于点E , 交直线l2于点D , 交x轴于点M , 且ED=2DM , 求a的值;(3)、如图2,点P是第四象限内一点,且∠BPO=135°,连接AP , 探究AP与BP之间的位置关系,并证明你的结论.
(1)、求点C的坐标;(2)、若平行于y轴的直线x=a交于直线1于点E , 交直线l2于点D , 交x轴于点M , 且ED=2DM , 求a的值;(3)、如图2,点P是第四象限内一点,且∠BPO=135°,连接AP , 探究AP与BP之间的位置关系,并证明你的结论.