高中数学人教新课标A版选修2-1 1.4全称量词与存在量词

试卷更新日期：2020-08-24 类型：同步测试

进入出卷网下载

一、单选题

1. 下列四个命题中的真命题为（）．

A、 $\forall x \in R ， x^{2} - 1 = 0$ B、 $\exists x \in Z ， 3 x - 1 = 0$ C、 $\forall x \in R ， x^{2} + 1 > 0$ D、 $\exists x \in Z ， 1 < 4 x < 3$

查看试题解析
2. 下列命题中是全称量词命题并且是真命题的是（）

A、 $\forall x \in R, x^{2} + 2 x + 1 > 0$ B、所有菱形的 $4$ 条边都相等 C、若 $2 x$ 为偶数，则 $x \in N$ D、 $π$ 是无理数

查看试题解析
3. 命题“ $\forall x \geq 1$ ， $x^{2} - 2 x + 1 \geq 0$ ”的否定是（）

A、 $\exists x_{0} \geq 1$ ， $x_{0}^{2} - 2 x_{0} + 1 < 0$ B、 $\exists x_{0} < 1$ ， $x_{0}^{2} - 2 x_{0} + 1 < 0$ C、 $\exists x_{0} \geq 1$ ， $x_{0}^{2} - 2 x_{0} + 1 \leq 0$ D、 $\exists x_{0} < 1$ ， $x_{0}^{2} - 2 x_{0} + 1 \leq 0$

查看试题解析
4. 命题“ $\exists x_{o} \in ∁_{R} Q ， x_{o}^{3} \in Q$ ”的否定是（）

A、∃x₀∈∁_RQ，x₀³∈Q B、 $\exists x_{o} \in ∁_{R} Q ， x_{o}^{3} \in Q$ C、 $\forall x \notin ∁_{R} Q ， x^{3} \notin Q$ D、 $\forall x \in ∁_{R} Q ， x^{3} \notin Q$

查看试题解析
5. 若“ $\exists x_{0} \in R$ ， $a x_{0}^{2} + 2 x_{0} + a < 0$ ”为真命题，则实数a的取值范围是（）

A、 $a < 1$ B、 $a \leq 1$ C、 $- 1 < a < 1$ D、 $- 1 < a \leq 1$

查看试题解析
6. 若对∀x∈[0，+∞），不等式2ax≤e^x﹣1恒成立，则实数a的最大值是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、1 D、2

查看试题解析
7. 下列说法不正确的是（）

A、若“p且q”为假，则p，q至少有一个是假命题 B、命题“∃x∈R，x²﹣x﹣1＜0”的否定是““∀x∈R，x²﹣x﹣1≥0” C、当a＜0时，幂函数y=x^a在（0，+∞）上单调递减 D、“φ= $\frac{π}{2}$ ”是“y=sin（2x+φ）为偶函数”的充要条件

查看试题解析
8. 已知命题 $p$ ： $\forall x \in$ R， $x^{2} - x + 1 < 0$ ；命题 $q$ ： $\exists x \in$ R， $x^{2} > 2^{x}$ ，则下列命题中为真命题的是（）

A、 $p \land q$ B、 $\neg p \land q$ C、 $p \land \neg q$ D、 $\neg p \land \neg q$

查看试题解析
9. 已知函数f（x）在R上单调递增，若∃x∈R，f（|x+1|）≤f（log₂a﹣|x+2|），则实数a的取值范围是（）

A、[2，+∞） B、[4，+∞） C、[8，+∞） D、（0，2]

查看试题解析
10. 若对任意 $m \in [0 ， 1]$ ，总存在唯一 $x \in [- 1 ， 1]$ 使得 $m + x^{2} e^{x} - a = 0$ 成立，则实数 $a$ 的取值范围是（）

A、 $[1 ， e]$ B、 $(1 + \frac{1}{e} ， e]$ C、 $(0 ， e]$ D、 $[1 + \frac{1}{e} ， e]$

查看试题解析
11. 已知：命题p：“a=1是 $x > 0 ， x + \frac{a}{x} \geq 2$ 的充分必要条件”；命题q：“ $\exists x \in R ， x^{2} + x - 2 > 0$ ，”则下列结论错误的是 ( )

A、命题“p∧q”是真命题 B、命题“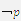（）∧q”是真命题 C、命题“p∧（ $\neg q$ ）”是真命题 D、命题“（ $\neg p$ )∧（ $\neg q$ ）”是真命题

查看试题解析
12. 已知命题p：“任意x∈[1,2]，x²－a≥0”，命题q：“存在x∈R，x²＋2ax＋2－a＝0”．若命题“p且q”是真命题，则实数a的取值范围为( )

A、a≤－2或a＝1 B、a≤－2或1≤a≤2 C、a≥1 D、－2≤a≤1

查看试题解析

二、多选题

13. 给出下列四个命题，其中正确的是（）

A、 $\forall x \in (- \infty, 0), 2^{x} > 3^{x}$ B、 $\forall x \in Q, \frac{1}{3} x^{2} + \frac{1}{2} x + 1 \in Q$ C、 $\exists α, β \in R,$ 使得 $\sin (α + β) = \sin α + \sin β$ D、 $\exists x, y \in Z$ ，使得 $x - 2 y = 10$

查看试题解析

三、填空题

14. 已知命题“ $\forall x \in R ， a x^{2} - a x + 1 > 0$ ”为真命题，则实数 $a$ 的取值范围是.

查看试题解析
15. 命题“∃x₀∈R, $4 x_{0}^{2} - a x_{0} + 1 < 0$ ”为假命题，则实数a的取值范围是．

查看试题解析
16. 若“ $\forall x \in [0, \frac{π}{4}]$ ， $tan x - 1 \leq m$ ”是真命题，则实数 $m$ 的最小值为.

查看试题解析
17. 若 $" \exists x \in [2, 8], m \leq \log_{2} x + 4 \log_{x} 2 "^{}$ 为真命题，则实数 $m$ 的最大值为．

查看试题解析

四、解答题

18. 判断下列命题是全称命题还是特称命题，并判断其真假；

(1)、 $\forall x \in N ， x^{4} + 1 > 2$ ；

(2)、 $\exists x_{0} \in Z ， {x_{0}}^{3} < 1$ .

查看试题解析
19. 判断下列命题是全称命题还是存在性命题，并写出它们的否定：

(1)、p：对任意的x∈R，x²+x+1=0都成立；

(2)、p：∃x∈R，x²+2x+5＞0．

查看试题解析
20. 是否存在整数m，使得命题“∀x∈R，m²﹣m＜x²+x+1”是真命题？若存在，求出m的值；若不存在，请说明理由．

查看试题解析
21. 已知命题 $p :$ “ $\forall x \in [1, 2]$ ， $x^{2} - a \geq 0$ ”；命题 $q :$ “ $\exists x \in R$ ， $x^{2} + 2 a x + 2 - a = 0$ ”，若命题“ $p \land q$ ”是真命题，求实数 $a$ 的取值范围.

查看试题解析
22. 已知命题 $p :$ 方程 $x^{2} - 2 m x + m = 0$ 没有实数根；命题 $q : \forall x \in R, x^{2} + m x + 1 \geq 0$ .

(1)、写出命题 $q$ 的否定“ $\neg q$ ”.

(2)、如果“ $p \lor q$ ”为真命题，“ $p \land q$ ”为假命题，求实数 $m$ 的取值范围.

查看试题解析
23. 已知 $p ： \forall x \in R$ ， $m (4 x^{2} + 1) > x$ ； $q ： \exists x \in [2 ， 8]$ ， $m \log_{2} x + 1 ⩾ 0$ .

(1)、若 $p$ 为真命题，求实数 $m$ 的取值范围；

(2)、若 $p$ 与 $q$ 的真假性相同，求实数 $m$ 的取值范围.

查看试题解析

高中数学人教新课标A版 选修2-1 1.4全称量词与存在量词

一、单选题

二、多选题

三、填空题

四、解答题

高中数学人教新课标A版选修2-1 1.4全称量词与存在量词