湖北省孝感市安陆市2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-08-24 类型:期末考试
一、选择题
-
1. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、2. 下列各组数中,能构成直角三角形的是( )A、4,5,6 B、1,1, C、6,8,11 D、5,12,233. 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,CD⊥AB于D,则CD的长是( )
 A、5 B、7 C、 D、4. 如图,直线 的解析式为 ,直线 的解析式为 ,则不等式 的解集是( )
A、5 B、7 C、 D、4. 如图,直线 的解析式为 ,直线 的解析式为 ,则不等式 的解集是( )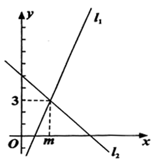 A、 B、 C、 D、5. 下列各数中,与 的积为有理数的是( )A、 B、 C、 D、6. 某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如表:
A、 B、 C、 D、5. 下列各数中,与 的积为有理数的是( )A、 B、 C、 D、6. 某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如表:尺码
39
40
41
42
43
平均每天销售数量(件)
10
12
20
12
12
该店主决定本周进货时,增加了一些尺码的衬衫,影响该店主决策的统计量是( )
A、众数 B、方差 C、平均数 D、中位数7. 甲、乙、丙、丁四位同学五次数学测验成绩统计如表.如果从这四位同学中,选出一位成绩较好且状态稳定的同学参加全国数学联赛,那么应选( )甲
乙
丙
丁
平均数
80
85
85
80
方 差
42
42
54
59
A、甲 B、乙 C、丙 D、丁8. 将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变,当 时,如图1,测得AC=2,当 时,如图2,则AC的值为( )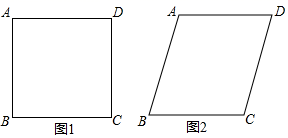 A、 B、 C、2 D、9. 如图,某工厂有甲,乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度与注水时间之间的函数关系图象可能是如图,某工厂有甲,乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度与注水时间之间的函数关系图象可能是( )
A、 B、 C、2 D、9. 如图,某工厂有甲,乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度与注水时间之间的函数关系图象可能是如图,某工厂有甲,乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度与注水时间之间的函数关系图象可能是( )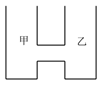 A、
A、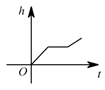 B、
B、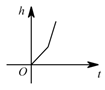 C、
C、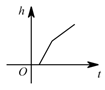 D、
D、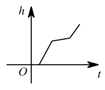 10. 如图,在平面直角坐标系中,平行四边形OABC的边OA在x轴的正半轴上,A,C两点的坐标分别为(2,0),(1,2),点B在第一象限,将直线 沿y轴向上平移m个单位.若平移后的直线与边BC有交点,则m的取值范围是( )
10. 如图,在平面直角坐标系中,平行四边形OABC的边OA在x轴的正半轴上,A,C两点的坐标分别为(2,0),(1,2),点B在第一象限,将直线 沿y轴向上平移m个单位.若平移后的直线与边BC有交点,则m的取值范围是( )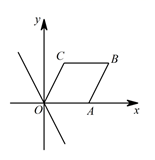 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
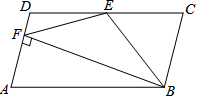
11. 有意义,则实数a的取值范围是.12. 菱形的面积是16,一条对角线长为4,则另一条对角线的长为.13. 已知一次函数的图象过点(3,5)与点(-4,-9),则这个一次函数的解析式为.14. 已知一组数据 a,b,c,d的方差是4,那么数据 , , , 的方差是.15. 《九章算术》卷九“勾股”中记载:今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽,问索长几何?译文:今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺.牵着绳索(绳索头与地面接触)退行,在距木根部8尺处时绳索用尽.问绳索长是多少?设绳索长为x尺,可列方程为 .16. 如图,在平行四边形ABCD中,AB=2AD,BE平分∠ABC交CD于点E,作BF⊥AD,垂足为F,连接EF,小明得到三个结论:①∠FBC=90°;②ED=EB;③ .则三个结论中一定成立的是.
三、解答题
-
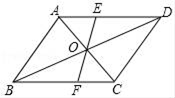
17. 计算:(1)、(2)、18. 已知x=2+ ,求代数式 的值.19. 已知平行四边形ABCD,对角线AC、BD交于点O,线段EF过点O交AD于点E,交BC于点F.求证:OE=OF.
 20. 为了解某校九年级学生的理化实验操作情况,随机抽查了40名同学实验操作的得分.根据获取的样本数据,制作了如下的条形统计图和扇形统计图.请根据相关信息,解答下列问题.
20. 为了解某校九年级学生的理化实验操作情况,随机抽查了40名同学实验操作的得分.根据获取的样本数据,制作了如下的条形统计图和扇形统计图.请根据相关信息,解答下列问题.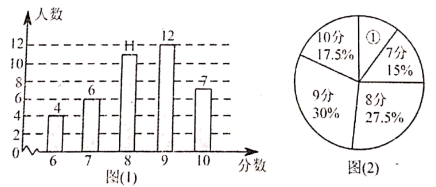 (1)、①中的描述应为“ 6分m% ”,其中的m值为;扇形①的圆心角的大小是;(2)、求这40个样本数据平均数、众数、中位数;(3)、若该校九年级共有160名学生,估计该校理化实验操作得满分的学生有多少人.21. 在平面直角坐标系中,原点为O,已知一次函数的图象过点A(0,5),点B(-1,4)和点P(m,n).(1)、求这个一次函数的解析式;(2)、当n=2时,求直线AB,直线OP与x轴围成的图形的面积;(3)、当 的面积等于 的面积的2倍时,求n的值.22. 如图,在正方形ABCD中,E是AD的中点,F是 AB上一点,且AF= AB.
(1)、①中的描述应为“ 6分m% ”,其中的m值为;扇形①的圆心角的大小是;(2)、求这40个样本数据平均数、众数、中位数;(3)、若该校九年级共有160名学生,估计该校理化实验操作得满分的学生有多少人.21. 在平面直角坐标系中,原点为O,已知一次函数的图象过点A(0,5),点B(-1,4)和点P(m,n).(1)、求这个一次函数的解析式;(2)、当n=2时,求直线AB,直线OP与x轴围成的图形的面积;(3)、当 的面积等于 的面积的2倍时,求n的值.22. 如图,在正方形ABCD中,E是AD的中点,F是 AB上一点,且AF= AB.求证:CE⊥EF.
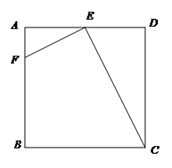 23. 现有两家可以选择的快递公司的收费方式如下.
23. 现有两家可以选择的快递公司的收费方式如下.甲公司:物品重量不超过1千克的,需付费20元,超过1千克的部分按每千克4元计价.
乙公司:按物品重量每千克7元计价,外加一份包装费10元.设物品的重量为x千克,甲、乙公司快递该物品的费用分别为 , .
 (1)、分别写出 和 与x的函数表达式(并写出x的取值范围);(2)、图中给出了 与x的函数图象,请在图中画出(1)中 与x的函数图象(要求列表,描点).
(1)、分别写出 和 与x的函数表达式(并写出x的取值范围);(2)、图中给出了 与x的函数图象,请在图中画出(1)中 与x的函数图象(要求列表,描点).x
…
…
y
…
…
24. 已知:如图,已知直线AB的函数解析式为 ,AB与y轴交于点A,与x轴交于点B.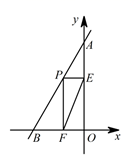 (1)、在答题卡上直接写出A,B两点的坐标;(2)、若点P(a,b)为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点 F,连接EF.问:
(1)、在答题卡上直接写出A,B两点的坐标;(2)、若点P(a,b)为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点 F,连接EF.问:①若 的面积为S,求S关于a的函数关系式;
② 是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.