湖北省东湖高新区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-08-24 类型:期末考试
一、选择题
-
1. 二次根式 在实数范围内有意义,则x的取值范围是( )A、x≥-3 B、x≠3 C、x≥0 D、x≠-32. 下面哪个点在函数y=2x-1的图象上( )A、(-2.5,-4) B、(1,3) C、(2.5,4) D、(0,1)3. 下列各组线段a、b、c中不能组成直角三角形的是( )A、a=8,b=15,c=17 B、a=7,b=24,c=25 C、a=40,b=50,c=60 D、a= ,b=4,c=54. 下列各式中,运算正确的是( )A、 B、 C、 D、5. 下列不能判断是正方形的有( )A、对角线互相垂直的矩形 B、对角线相等的矩形 C、对角线互相垂直且相等的平行四边形 D、对角线相等的菱形6. 交警在一个路口统计的某个时段来往车辆的分布如条形图所示.请找出这些车辆速度的众数、中位数分别是( )
 A、52,53 B、52,52 C、53,52 D、52, 517. 已知直线y=kx+b经过一、二、三象限,则直线y=bx-k-2的图象只能是( )A、
A、52,53 B、52,52 C、53,52 D、52, 517. 已知直线y=kx+b经过一、二、三象限,则直线y=bx-k-2的图象只能是( )A、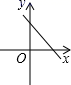 B、
B、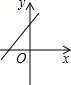 C、
C、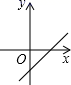 D、
D、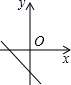 8. 菱形的周长等于其高的8倍,则这个菱形的较大内角是( )A、30° B、120° C、150° D、135°9. 如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省( )元
8. 菱形的周长等于其高的8倍,则这个菱形的较大内角是( )A、30° B、120° C、150° D、135°9. 如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省( )元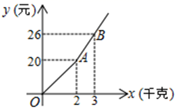 A、3 B、4 C、5 D、610. 矩形ABCD中,AD= AB,AF平分∠BAD,DF⊥AF于点F,BF交CD于点H.若AB=6,则CH=( )
A、3 B、4 C、5 D、610. 矩形ABCD中,AD= AB,AF平分∠BAD,DF⊥AF于点F,BF交CD于点H.若AB=6,则CH=( )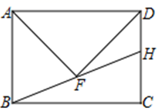 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 化简:= .
12. 甲、乙、丙、丁四人进行100m短跑训练,统计近期10次测试的平均成绩都是13.2s,10次测试成绩的方差如下表:则这四人中发挥最稳定的是.选手
甲
乙
丙
丁
方差(S2)
0.020
0.019
0.021
0.022
13. 我国古代数学著作《九章算术》有一个问题:一根竹子高1丈,折断后竹子顶端落在离竹子底端3尺处,1丈=10尺,那么折断处离地面的高度是尺.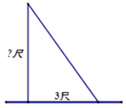 14. 如图,在正方形ABCD的右边作等腰三角形ADE,AD=AE, ,连BE,则 .
14. 如图,在正方形ABCD的右边作等腰三角形ADE,AD=AE, ,连BE,则 .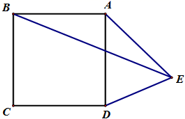 15. 如图,直线y=-x+m与y=nx+4n的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的解集为.
15. 如图,直线y=-x+m与y=nx+4n的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的解集为.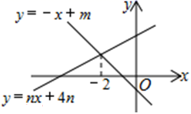 16. 如图,边长为4的菱形ABCD中,∠ABC=30°,P为BC上方一点,且 ,则PB+PC的最小值为.
16. 如图,边长为4的菱形ABCD中,∠ABC=30°,P为BC上方一点,且 ,则PB+PC的最小值为.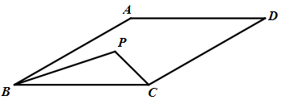
三、解答题
-
17. 计算:(1)、 ;(2)、18. 如图,平行四边形ABCD的对角线AC,BD相交于点O,E、F分别是OA、OC的中点.
求证:BE=DF
 19. 根据下列条件分别确定函数y=kx+b的解析式:(1)、y与x成正比例,当x=5时,y=6;(2)、直线y=kx+b经过点(3,6)与点(2,-4).20. 今年受疫情影响,我市中小学生全体在家线上学习.为了了解学生在家主动锻炼身体的情况,某校随机抽查了部分学生,对他们每天的运动时间进行调查,并将调查统计的结果分为四类:每天运动时间t≤20分钟的学生记为A类,20分钟<t≤40分钟记为B类,40分钟<t≤60分钟记为C类,t>60分钟记为D类.收集的数据绘制如下两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
19. 根据下列条件分别确定函数y=kx+b的解析式:(1)、y与x成正比例,当x=5时,y=6;(2)、直线y=kx+b经过点(3,6)与点(2,-4).20. 今年受疫情影响,我市中小学生全体在家线上学习.为了了解学生在家主动锻炼身体的情况,某校随机抽查了部分学生,对他们每天的运动时间进行调查,并将调查统计的结果分为四类:每天运动时间t≤20分钟的学生记为A类,20分钟<t≤40分钟记为B类,40分钟<t≤60分钟记为C类,t>60分钟记为D类.收集的数据绘制如下两幅不完整的统计图,请根据图中提供的信息,解答下列问题: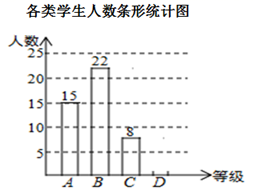
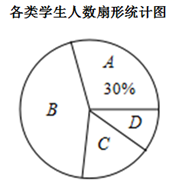 (1)、这次共抽取了名学生进行调查统计;(2)、将条形统计图补充完整,扇形统计图中D类所对应的扇形圆心角大小为;(3)、如果该校共有3000名学生,请你估计该校B类学生约有多少人?21. 如图,方格纸中每个小正方形的边长均为1,我们把每个小正方形的顶点叫做格点. 如:线段AB的两个端点都在格点上.
(1)、这次共抽取了名学生进行调查统计;(2)、将条形统计图补充完整,扇形统计图中D类所对应的扇形圆心角大小为;(3)、如果该校共有3000名学生,请你估计该校B类学生约有多少人?21. 如图,方格纸中每个小正方形的边长均为1,我们把每个小正方形的顶点叫做格点. 如:线段AB的两个端点都在格点上.
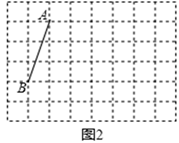
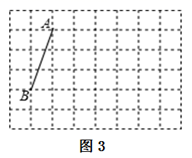 (1)、在图1中画一个以AB为边的平行四边形ABCD,点C、D在格点上,且平行四边形ABCD的面积为15;(2)、在图2中画一个以AB为边的菱形ABEF(不是正方形),点E、F在格点上,则菱形ABEF的对角线AE= , BF=;(3)、在图3中画一个以AB为边的矩形ABMN(不是正方形),点M、N在格点上,则矩形ABMN的长宽比 =.22. A城有肥料200t,B城有肥料300t.现要把这些肥料全部运往C、D两乡,C乡需要肥料240t,D乡需要肥料260t,其运往C、D两乡的运费如下表:
(1)、在图1中画一个以AB为边的平行四边形ABCD,点C、D在格点上,且平行四边形ABCD的面积为15;(2)、在图2中画一个以AB为边的菱形ABEF(不是正方形),点E、F在格点上,则菱形ABEF的对角线AE= , BF=;(3)、在图3中画一个以AB为边的矩形ABMN(不是正方形),点M、N在格点上,则矩形ABMN的长宽比 =.22. A城有肥料200t,B城有肥料300t.现要把这些肥料全部运往C、D两乡,C乡需要肥料240t,D乡需要肥料260t,其运往C、D两乡的运费如下表:C(元/t)
D(元/t)
A
20
30
B
10
15
设从A城运往C乡的肥料为xt,从A城运往两乡的总运费为y1元,从B城运往两乡的总运费为y2元.
(1)、分别写出y1、y2与x之间的函数关系式(不要求写自变量的取值范围);(2)、试比较A、B两城总运费的大小;(3)、若B城的总运费不得超过3800元,怎样调运使两城总费用的和最少?并求出最小值.23. 在矩形ABCD中,E是AD延长线上一点,F、G分别为EC、AD的中点,连接BG、CG、BE、FG.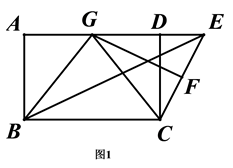
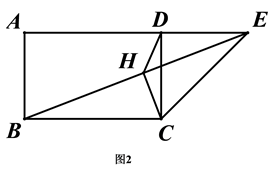 (1)、如图1,① 求证:BG=CG;
(1)、如图1,① 求证:BG=CG;② 求证:BE=2FG;
(2)、如图2,若ED=CD,过点C作CH⊥BE于点H,若BC=4,∠EBC=30°,则EH的长为.24. 已知,在平面直角坐标系中,一次函数y=kx-3(k≠0)交x轴于点A,交y轴与点B.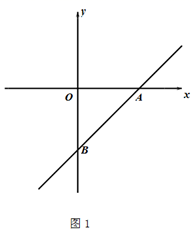
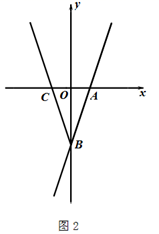
 (1)、如图1,若k=1,求线段AB的长;(2)、如图2,点C与点A关于y轴对称,作射线BC;
(1)、如图1,若k=1,求线段AB的长;(2)、如图2,点C与点A关于y轴对称,作射线BC;①若k=3,请写出以射线BA和射线BC所组成的图形为函数图象的函数解析式;
② y轴上有一点D(0,3),连接AD、CD,请判断四边形ABCD的形状并证明;若 ≥9,求k的取值范围