河南省驻马店市上蔡县2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2020-08-24 类型：期末考试

进入出卷网下载

一、选择题

1. 下列各式 $\frac{1}{2} x y$ ， $\frac{a + b}{2}$ ， $\frac{1}{π}$ ， $\frac{2 m - n}{4}$ ， $\frac{s + 1}{s - 1}$ ，分式有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 世界上能制造出的最小晶体管的长度只有0.00000004，用科学记数法表示为（）

A、 $4 \times 10^{- 8}$ 米 B、 $4 \times 10^{- 9}$ 米 C、 $0.4 \times 10^{9}$ 米 D、 $40 \times 10^{- 7}$ 米

查看试题解析
3. 方程 $\frac{1}{x - 1} - \frac{3}{2 x + 3} = 0$ 的解的情况为（）

A、 $x = 2$ B、 $x = 3$ C、 $x = 6$ D、 $x = 8$

查看试题解析
4. 在平面直角坐标系中，若点 $A (a, - b)$ 在第一象限内，则点 $B (- a, b)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 若点 $A (- 5, y_{1})$ 和点 $B (- 2, y_{2})$ 都在 $y = - \frac{1}{2} x + b$ 的图象上，那么 $y_{1}$ 与 $y_{2}$ 的大小关系是（）

A、 $y_{1} \leq y_{2}$ B、 $y_{1} = y_{2}$ C、 $y_{1} < y_{2}$ D、 $y_{1} > y_{2}$

查看试题解析
6. 下列说法正确的个数是（）
①对角线互相垂直或有一组邻边相等的矩形是正方形；②对角线相等或有一个角是直角的菱形是正方形；③对角线互相垂直且相等的平行四边形是正方形；④对角线互相垂直平分且相等的四边形是正方形.

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 某演讲比赛中，评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分，然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例计算选手的综合成绩.某选手的演讲内容、演讲能力、演讲效果成绩依次为85、90、95，则该选手的综合成绩为（）

A、92 B、88 C、90 D、95

查看试题解析
8. 如图，在平行四边形ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，若BF=6，AB=5，则AE的长为（）

A、4 B、8 C、6 D、10

查看试题解析
9. 学校为创建“书香校园”购买了一批图书．已知购买科普类图书花费10000元，购买文学类图书花费9000元，其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元，且购买科普书的数量比购买文学书的数量少100本．求科普类图书平均每本的价格是多少元？若设科普类图书平均每本的价格是x元，则可列方程为（）

A、 $\frac{10000}{x}$ ﹣ $\frac{9000}{x - 5}$ =100 B、 $\frac{9000}{x - 5}$ ﹣ $\frac{10000}{x}$ =100 C、 $\frac{10000}{x - 5}$ ﹣ $\frac{9000}{x}$ =100 D、 $\frac{9000}{x}$ ﹣ $\frac{10000}{x - 5}$ =100

查看试题解析
10. 如图，在平面直角坐标系中，正方形 $A B C O$ 的顶点O在坐标原点，点B的坐标为 $(2 ， 4)$ ，点A在第二象限，反比例函数 $y = \frac{k}{x}$ 的图象经过点A，则k的值是（）

A、－2 B、－3 C、－4 D、4

查看试题解析

二、填空题

11. 计算： ${(- 45)}^{2} + {(- \frac{1}{2})}^{- 3} + {(- \frac{1}{2})}^{0} + | - 1 | =$ .

查看试题解析
12. 若分式方程 $\frac{m}{x - 2} - \frac{2 x}{2 - x} = 1$ 会产生增根，则m的值为.

查看试题解析
13. 如图，点P是矩形 $A B C D$ 的对角线 $A C$ 上一点，过点P作 $E F // B C$ 分别交 $A B$ 、 $C D$ 于E、F，连接 $P B$ ， $P D$ .若 $A E = 2$ ， $P F = 8$ .则图中阴形部分的面积为.

查看试题解析
14. 已知直线 $y = a x + b$ 与 $y = - 2 x + 3$ 平行，且与y轴的交点坐标是 $(0, 5)$ ，则 $a b =$ .

查看试题解析
15. 如图，直线 $y = - \frac{3}{4} x + 3$ 与 $x$ 轴、 $y$ 轴分别相交于点A、B，点M在x轴上且不同于点A，点N是平面直角坐标系中的第一象限内任意一点.如果以A，B，M，N为顶点的四边形是菱形，那么满足条件的点M的坐标是.

查看试题解析

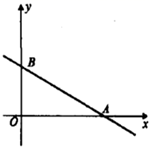
三、解答题

16. 先化简再求值： $(\frac{x^{2} - x}{x^{2} - 2 x + 1} - \frac{2}{x - 1}) \div \frac{x^{2} - 2 x}{(x - 1) (x + 2)} + 2020$ ，然后在 $- \sqrt{5} < x < \sqrt{5}$ 的范围内选取一个合适的整数作为 $x$ 的值并代入求值.

查看试题解析
17. 如图，一次函数 $y = k x + b$ （ $k \neq 0$ ）的图象经过点 $A (- 2 ， 6)$ ，且与 $x$ 轴相交于点B，与正比例函数 $y = 3 x$ 的图象相交于点C，点C的横坐标为1.

(1)、求一次函数 $y = k x + b$ （ $k \neq 0$ ）的表达式；

(2)、若点D在x轴负半轴上，且满足 $S_{Δ C O D} = 2 S_{Δ B O C}$ ，求点D的坐标

查看试题解析
18. 在学校举办的一次文艺汇演比赛中，八（1）班和八（2）班参加表演比赛的女生身高（单位： $cm$ ）分别是：
八（1）班：163，164，165，165，165，165，166，167.

八（2）班：162，164，164，165，166，166，166，167.

(1)、把表格补充完整

身高

班级

平均数

中位数

众数

八（1）班

165

165

165

八（2）班

165

(2)、从数据来看，哪个班女生的身高更整齐？请你从方差的角度说明理由.

查看试题解析
19. 如图，在▱ABCD中，点O是边BC的中点，连接DO并延长，交AB延长线于点E，连接BD，EC．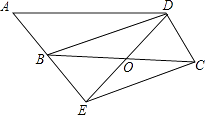

(1)、求证：四边形BECD是平行四边形；

(2)、若∠A=50°，则当∠BOD=°时，四边形BECD是矩形．

查看试题解析
20. 某商场购进甲、乙两种商品，甲种商品共用了2000元，乙种商品共用了2400元.已知乙种商品每件进价比甲种商品每件进价多8元，且购进的甲、乙两种商品件数相同.

(1)、求甲、乙两种商品的每件进价；

(2)、该商场将购进的甲、乙两种商品进行销售，甲种商品的销售单价为80元，乙种商品的销售单价为88元，销售过程中发现甲种商品销量不好，商场决定：甲种商品销售一定数量后，将剩余的甲种商品按原销售单价的七折销售；乙种商品销售单价保持不变，要使两种商品全部售完后共获利不少于3520元，问甲种商品按原销售单价至少销售多少件？

查看试题解析
21. 如图，平面直角坐标系中，一次函数 $y_{1} = a x + b$ （ $a \neq 0$ ）的图象与反比例函数 $y_{2} = \frac{k}{x}$ （ $k \neq 0$ ）的图象交于点 $A (1 ， 2)$ 和 $B (- 2 ， m)$ .

(1)、求一次函数和反比例函数的表达式；

(2)、请直接写出 $y_{1} > y_{2}$ 时x的取值范围；

(3)、过点B作 $B E // x$ 轴， $A D ⊥ B E$ 于点D，点C是直线 $B E$ 上一点，若 $A D = 3 C D$ ，求点C的坐标.

查看试题解析
22. 如图①， $∠ Q P N$ 的顶点P在正方形 $A B C D$ 两条对角线的交点处， $∠ Q P N = α$ ，将 $∠ Q P N$ 绕点P旋转，旋转过程中 $∠ Q P N$ 的两边分别与正方形 $A B C D$ 的边 $A D$ 和 $C D$ 交于点E和点F（点F与点C、D不重合）.

(1)、如图①，当 $α = 90 °$ 时， $D E$ 、 $D F$ 、 $A D$ 之间满足的数量关系是；

(2)、如图②，将图①中的正方形 $A B C D$ 改为 $∠ A D C = 120 °$ 的菱形，其他条件不变，当 $α = 60 °$ 时，（1）中的结论变为 $D E + D F = \frac{1}{2} A D$ ，并给出证明过程；

(3)、在（2）的条件下，若旋转过程中 $∠ Q P N$ 的边 $P Q$ 与边 $A D$ 的延长线交于点E，其他条件不变，探究在整个运动变化过程中， $D E$ 、 $D F$ 、 $A D$ 之间满足的数量关系，直接写出结论，不用加以证明.

查看试题解析
23. 如图，四边形 $A B C D$ 的四个顶点分别在反比例函数 $y = \frac{m}{x}$ 与 $y = \frac{n}{x}$ （ $x > 0$ ， $0 < m < n$ ）的图象上，对角线 $B D // y$ 轴，且 $B D ⊥ A C$ 于点P，已知点B的横坐标为4.

(1)、当 $m = 4$ ， $n = 16$ 时.
①若点 $P$ 的纵坐标为2，求直线 $A B$ 的函数表达式.

②若点P是 $B D$ 的中点，试判断四边形 $A B C D$ 的形状，并说明理由.

(2)、四边形 $A B C D$ 能否成为正方形？若能，求此时m、n之间的数量关系：若不能，试说明理由.

查看试题解析