河南省信阳市淮滨县2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-08-24 类型:期末考试
一、选择题
-
1. 下列二次根式中,能与 合并的是( )A、 B、 C、 D、2. 要使式子 有意义,则x的取值范围是( )A、x>0 B、x≥﹣3 C、x≥3 D、x≤33. 如图,将一根长为24cm的筷子,置于底面直径为5cm,高为12cm的圆柱水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是( )
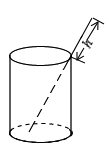 A、12cm≤h≤19cm B、12cm≤h≤13cm C、11cm≤h≤12cm D、5cm≤h≤12cm4. 如图,在矩形ABCD中,AC是对角线,将ABCD绕点B顺时针旋转90°到GBEF位置,H是EG的中点,若AB=6,BC=8,则线段CH的长为( )
A、12cm≤h≤19cm B、12cm≤h≤13cm C、11cm≤h≤12cm D、5cm≤h≤12cm4. 如图,在矩形ABCD中,AC是对角线,将ABCD绕点B顺时针旋转90°到GBEF位置,H是EG的中点,若AB=6,BC=8,则线段CH的长为( )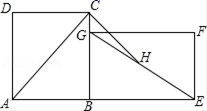 A、2 B、 C、2 D、5. 如图,把一个长方形的纸片对折两次,然后剪下一个角,要得到一个正方形,剪口与折痕所成锐角的大小为( )
A、2 B、 C、2 D、5. 如图,把一个长方形的纸片对折两次,然后剪下一个角,要得到一个正方形,剪口与折痕所成锐角的大小为( )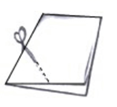 A、 B、 C、 D、6. 在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,下列条件中不能说明△ABC是直角三角形的是( )A、a=32 , b=42 , c=52 B、a=9,b=12,c=15 C、∠A:∠B:∠C=5:2:3 D、∠C﹣∠B=∠A7. 下列各曲线中,不表示y是x的函数的是( )A、
A、 B、 C、 D、6. 在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,下列条件中不能说明△ABC是直角三角形的是( )A、a=32 , b=42 , c=52 B、a=9,b=12,c=15 C、∠A:∠B:∠C=5:2:3 D、∠C﹣∠B=∠A7. 下列各曲线中,不表示y是x的函数的是( )A、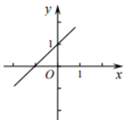 B、
B、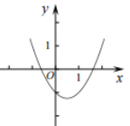 C、
C、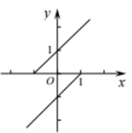 D、
D、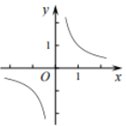 8. 如图,直线y=ax+b过点A(0,2)和点B(﹣3,0),则方程ax+b=0的解是( )
8. 如图,直线y=ax+b过点A(0,2)和点B(﹣3,0),则方程ax+b=0的解是( )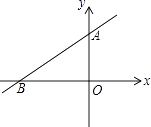 A、x=2 B、x=0 C、x=﹣1 D、x=﹣39. 某校有21名同学参加比赛,预赛成绩各不相同,要取前11名参加决赛,小颖已经知道了自己的成绩,她想知道自己能否进入决赛,只需再知道这21名同学成绩的( )A、中位数 B、众数 C、平均数 D、最高分10. 已知一组数据a、b、c的平均数为5,方差为4,那么数据a+2、b+2、c+2的平均数和方差分别为( )A、7,6 B、7,4 C、5,4 D、以上都不对
A、x=2 B、x=0 C、x=﹣1 D、x=﹣39. 某校有21名同学参加比赛,预赛成绩各不相同,要取前11名参加决赛,小颖已经知道了自己的成绩,她想知道自己能否进入决赛,只需再知道这21名同学成绩的( )A、中位数 B、众数 C、平均数 D、最高分10. 已知一组数据a、b、c的平均数为5,方差为4,那么数据a+2、b+2、c+2的平均数和方差分别为( )A、7,6 B、7,4 C、5,4 D、以上都不对二、填空题
-
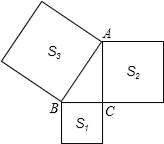
11. 一组数据2,6,5,2,4,则这组数据的平均数是.12. 如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1、S2、S3 , 且S1=5,S2=6,则AB的长为.
 13. 某楼梯如图所示,欲在楼梯上铺设红色地毯,已知这种地毯每平方米售价为30元,楼梯宽为2m,则购买这种地毯至少需要元.
13. 某楼梯如图所示,欲在楼梯上铺设红色地毯,已知这种地毯每平方米售价为30元,楼梯宽为2m,则购买这种地毯至少需要元.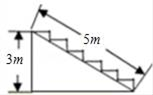 14. 如图,在平行四边形ABCD中,∠BAD的平分线AE交BC于点E , 且BE=3.若平行四边形ABCD的周长是16,则EC的长为 .
14. 如图,在平行四边形ABCD中,∠BAD的平分线AE交BC于点E , 且BE=3.若平行四边形ABCD的周长是16,则EC的长为 .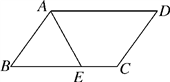 15. 如图,正方形 的边长为8,点E是 上的一点,连接 并延长交射线 于点F,将 沿直线 翻折,点B落在点N处, 的延长线交 于点M,当 时,则 的长为.
15. 如图,正方形 的边长为8,点E是 上的一点,连接 并延长交射线 于点F,将 沿直线 翻折,点B落在点N处, 的延长线交 于点M,当 时,则 的长为.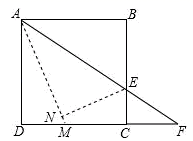
三、解答题
-
16. 先化简,再求值: ,其中m=4.17. 如图,已知在四边形ABCD中,AE⊥BD于E,CF⊥BD于F,AE=CF,BF=DE,求证:四边形ABCD是平行四边形.
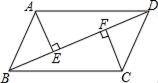 18. 如图,在四边形 中, , , .求证: .
18. 如图,在四边形 中, , , .求证: .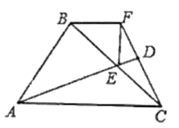 19. 在平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=-x+4的交点为P(3,m),与y轴交于点A .(1)、求m的值;(2)、如果△PAO的面积为3,求直线y=kx+b的表达式.20. 如图,正方形ABCD的边长为2 ,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F.
19. 在平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=-x+4的交点为P(3,m),与y轴交于点A .(1)、求m的值;(2)、如果△PAO的面积为3,求直线y=kx+b的表达式.20. 如图,正方形ABCD的边长为2 ,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F.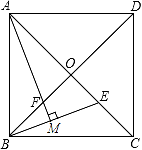 (1)、求证:AF=BE;(2)、求点E到BC边的距离.21. 中考体育测试前,雁塔区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽取了本区部分选报引体向上项目的初三男生,并将测试得到的成绩绘成了下面两幅不完整的统计图.
(1)、求证:AF=BE;(2)、求点E到BC边的距离.21. 中考体育测试前,雁塔区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽取了本区部分选报引体向上项目的初三男生,并将测试得到的成绩绘成了下面两幅不完整的统计图.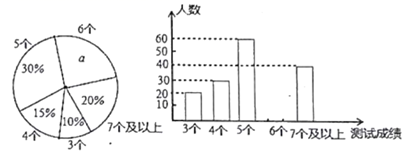
请你根据图中的信息,解答下列问题:
(1)、写出扇形图中a= , 并补全条形图;(2)、在这次抽测中,测试成绩的众数和中位数分别是个、个;(3)、该区体育中考选报引体向上的男生共有2400人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?22.甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买60元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.
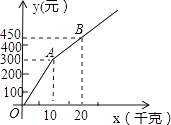 (1)、甲、乙两采摘园优惠前的草莓销售价格是每千克元;(2)、求y1、y2与x的函数表达式;(3)、在图中画出y1与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围.23. 如图,平面直角坐标系中,直线1分别交x轴、y轴于A、B两点,点A的坐标为 , ,过点B的直线 与x轴交于点C.
(1)、甲、乙两采摘园优惠前的草莓销售价格是每千克元;(2)、求y1、y2与x的函数表达式;(3)、在图中画出y1与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围.23. 如图,平面直角坐标系中,直线1分别交x轴、y轴于A、B两点,点A的坐标为 , ,过点B的直线 与x轴交于点C.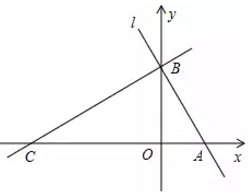 (1)、求直线l的解析式及点C的坐标.(2)、点D在x轴上从点C向点A以每秒1个单位长的速度运动( ),过点D分别作 , , 交 、 于点E、F,连接 ,点G为 的中点.
(1)、求直线l的解析式及点C的坐标.(2)、点D在x轴上从点C向点A以每秒1个单位长的速度运动( ),过点D分别作 , , 交 、 于点E、F,连接 ,点G为 的中点.①判断四边形 的形状并证明;
②求出t为何值时线段DG的长最短.
(3)、点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,说明理由.