河南省洛阳市洛宁县2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-08-24 类型:期末考试
一、选择题
-
1. 若分式 有意义,则x的取值范围是( )A、 B、 C、 D、2. 将 这三个数按从小到大的顺序排列,结果正确的是( )A、 B、 C、 D、3. PM2.5是指大气中直径0.0000025米的颗粒物,将0.0000025用科学记数法表( )A、2.5×10﹣7 B、2.5×10-6 C、25×10﹣7 D、0.25×10﹣54. 下表记录了甲、乙、丙、丁四名同学参加某区“中华魂”主题教育演讲比赛的相关数据:根据表中数据,要从中选择一名成绩好且发挥稳定的同学参加市级比赛,应该选择
甲
乙
丙
丁
平均数 分
90
80
90
80
方差
2.4
2.2
5.4
2.4
A、甲 B、乙 C、丙 D、丁5. 正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )A、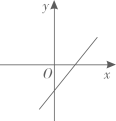 B、
B、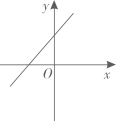 C、
C、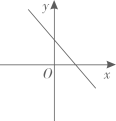 D、
D、 6. 如图,点A在反比例函数 的图象上, 轴于点B,点C在x轴的负半轴上,且 ,若 的面积为18,则k的值为( )
6. 如图,点A在反比例函数 的图象上, 轴于点B,点C在x轴的负半轴上,且 ,若 的面积为18,则k的值为( )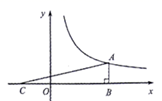 A、12 B、18 C、20 D、247. 下列判断错误的是( )A、两组对边分别相等的四边形是平行四边形 B、四个内角都相等的四边形是矩形 C、四条边都相等的四边形是菱形 D、两条对角线垂直且平分的四边形是正方形8. 如图所示,平行四边形ABCD中,AC的垂直平分线交于点E,且 CDE的周长为8,则平行四边形ABCD的周长是( )
A、12 B、18 C、20 D、247. 下列判断错误的是( )A、两组对边分别相等的四边形是平行四边形 B、四个内角都相等的四边形是矩形 C、四条边都相等的四边形是菱形 D、两条对角线垂直且平分的四边形是正方形8. 如图所示,平行四边形ABCD中,AC的垂直平分线交于点E,且 CDE的周长为8,则平行四边形ABCD的周长是( ) A、10 B、12 C、14 D、169. 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
A、10 B、12 C、14 D、169. 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )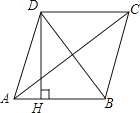 A、 B、 C、5 D、410. 如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=12,AB=10,则AE的长为( )
A、 B、 C、5 D、410. 如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=12,AB=10,则AE的长为( ) A、16 B、15 C、14 D、13
A、16 B、15 C、14 D、13二、填空题
-
11. 计算: + = .12. 在平行四边形ABCD中,∠B+∠D=200°,则∠A的度数为.13. 已知正比例函数:y = (3m-2)x的图像上两点A(x1 , y1),B(x2 , y2),当x1 < x2时,有y1 >y2那么m的取值范围是.14. 如果一组数据﹣3,﹣2,0,1,x,6,9,12的平均数为3,那么这组数据的中位数是.15. 如图,正方形ABCD的边长为4,E是边BC上的一点且BE=1,P为对角线AC上的一动点,连接PB,PE,当点P在AC上运动时,△PBE周长的最小值是.

三、解答题
-
16. 先化简,再求值: - ),其中a=2,b= 317. 某校初一开展英语拼写大赛,爱国班和求知班根据初赛成绩,各选出5名选手参加复赛,两个班备选出的5名选手的复赛成绩如图所示:
班级
平均数(分)
中位数(分)
众数(分)
爱国班
a
85
c
求知班
85
b
100
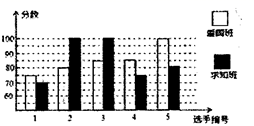 (1)、根据图示直接写出a , b , c的值:(2)、已知爱国班复赛成绩方差是70,请求出求知班复赛成绩的方差,并说明哪个班成绩比较稳定?18. 已知:一次函数y=kx+b的图象经过M(0,2),(1,3)两点.(1)、求k,b的值;(2)、若一次函数y=kx+b的图象与x轴交点为A(a,0),求a的值.19. 如图.在平面直角坐标系中,直线y = x +b与双曲线y = 相交于AB两点,已知A (2,5),B(-5,m).求:
(1)、根据图示直接写出a , b , c的值:(2)、已知爱国班复赛成绩方差是70,请求出求知班复赛成绩的方差,并说明哪个班成绩比较稳定?18. 已知:一次函数y=kx+b的图象经过M(0,2),(1,3)两点.(1)、求k,b的值;(2)、若一次函数y=kx+b的图象与x轴交点为A(a,0),求a的值.19. 如图.在平面直角坐标系中,直线y = x +b与双曲线y = 相交于AB两点,已知A (2,5),B(-5,m).求: (1)、求一次函数与反比例函数的表达式;(2)、 OAB的面积.20. 如图所示,O是平行四边形ABCD对角线的交点,过点O的直线EF分别交AD, BC于F,E两点,连结AE,CF,求证:四边形AECF是平行四边形.
(1)、求一次函数与反比例函数的表达式;(2)、 OAB的面积.20. 如图所示,O是平行四边形ABCD对角线的交点,过点O的直线EF分别交AD, BC于F,E两点,连结AE,CF,求证:四边形AECF是平行四边形.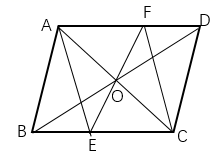 21. 如图所示,在矩形 中, 平分 .
21. 如图所示,在矩形 中, 平分 .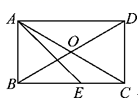 (1)、求 的度数;(2)、求证: .
(1)、求 的度数;(2)、求证: .