江西省新余市2019-2020学年高二下学期理数期末考试试卷
试卷更新日期:2020-08-21 类型:期末考试
一、单选题
-
1. 已知复数 ,则 ( )A、 B、 C、 D、22. “ ”是“方程 表示双曲线”的( )A、充分不必要条件 B、充要条件 C、必要不充分条件 D、既不充分也不必要条件3. 用反证法证明命题“三角形的内角中至少有一个角不大于 ”时,应假设( )A、三角形的三个内角都不大于 B、三角形的三个内角都大于 C、三角形的三个内角至多有一个大于 D、三角形的三个内角至少有两个大于4. 抛物线 的焦点为 ,点 是 上一点, ,则 ( )A、 B、 C、 D、5. 由 与x轴围成的封闭图形绕x轴旋转一周所得旋转体的体积是( )A、 B、 C、 D、6. 函数y= 的图象大致是( )A、
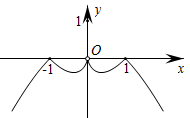
B、
B、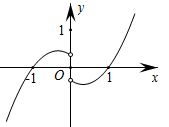
C、
C、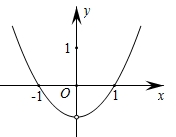
D、
D、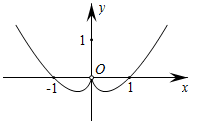
7. 我国古代数学名著《九章算术》中割圆术有:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣,”其体现的是一种无限与有限的转化过程,比如在 中“…”.即代表无限次重复,但原式却是个定值x,这可以通过方程 确定出来 ,类似地不难得到 ( )A、 B、 C、 D、8. 已知函数 , , ,…, , ,那么 ( )A、 B、 C、 D、9. 已知定义在R上的函数 满足 ,且 恒成立,则不等式 的解集为( )A、 B、 C、 D、10. 直三棱柱ABC-A1B1C1中,∠BCA=90°,M , N分别是A1B1 , A1C1的中点,BC=CA=CC1 , 则BM与AN所成角的余弦值为( )A、 B、 C、 D、11. 设双曲线 的左、右焦点分别为F1 , F2 , 过点F2的直线分别交双曲线左、右两支于点P,Q,点M为线段PQ的中点,若P,Q,F1都在以M为圆心的圆上,且 ,则双曲线C的离心率为( )
7. 我国古代数学名著《九章算术》中割圆术有:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣,”其体现的是一种无限与有限的转化过程,比如在 中“…”.即代表无限次重复,但原式却是个定值x,这可以通过方程 确定出来 ,类似地不难得到 ( )A、 B、 C、 D、8. 已知函数 , , ,…, , ,那么 ( )A、 B、 C、 D、9. 已知定义在R上的函数 满足 ,且 恒成立,则不等式 的解集为( )A、 B、 C、 D、10. 直三棱柱ABC-A1B1C1中,∠BCA=90°,M , N分别是A1B1 , A1C1的中点,BC=CA=CC1 , 则BM与AN所成角的余弦值为( )A、 B、 C、 D、11. 设双曲线 的左、右焦点分别为F1 , F2 , 过点F2的直线分别交双曲线左、右两支于点P,Q,点M为线段PQ的中点,若P,Q,F1都在以M为圆心的圆上,且 ,则双曲线C的离心率为( ) A、 B、2 C、 D、212. 若对任意的 , , , 恒成立,则a的最小值为( )A、 B、 C、 D、
A、 B、2 C、 D、212. 若对任意的 , , , 恒成立,则a的最小值为( )A、 B、 C、 D、二、填空题
-
13. 函数 ( )在 处有极值,则曲线 在原点处的切线方程是 .14. 已知直线l与平面 垂直,直线 的一个方向向量为 ,向量 与平面 平行,则 .15. 已知 是函数 的导函数,定义 为 的导函数,若方程 有实数解 ,则称点 为函数 的拐点,经研究发现,所有的三次函数 都有拐点,且都有对称中心,其拐点就是对称中心,设 ,若点 是函数 的“拐点”也是函数 图像上的点,则 .16. 如图,在一个60°的二面角的棱上有两个点A,B,AC,BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4,AC=6,BD=8,则CD的长为 .

三、解答题
-
17. 已知实数 ,p: ,q:(1)、若 是 的必要不充分条件,求实数m的取值范围;(2)、若 , 为真命题,求实数x的取值范围.18. 已知数列 前n项和为 ,且 .(1)、试求出 , , , ,并猜想 的表达式.(2)、用数学归纳法证明你的猜想.19. 如图,在四棱锥 中,平面 平面 , , , , , , .

(Ⅰ)求证: 平面 ;
(Ⅱ)求直线 与平面 所成角的正弦值.
20. 把边长为6的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为 ,容积为 . (1)、写出函数 的解析式,并求出函数的定义域;(2)、求当x为多少时,容器的容积最大?并求出最大容积.
(1)、写出函数 的解析式,并求出函数的定义域;(2)、求当x为多少时,容器的容积最大?并求出最大容积.