黑龙江省齐齐哈尔市2019-2020学年高二下学期理数期末考试试卷
试卷更新日期:2020-08-21 类型:期末考试
一、单选题
-
1. 复数 ( )A、 B、 C、 D、2. 已知函数 的导函数为 ,且e为自然对数的底数,则 =( )A、2 B、1 C、0 D、e3. 有一段“三段论”推理是这样的:对于可导函数 ,如果 ,那么 是函数 的极值点.因为函数 在 处的导数值 ,所以 是函数 的极值点.以上推理中( )A、小前提错误 B、大前提错误 C、推理形式错误 D、结论正确4. 展开式的第5项的系数为( )A、15 B、﹣60 C、60 D、﹣155. 下列说法错误的是( )A、在回归分析中,回归直线始终过样本点( x1 , y1 ),( x2 , y2 ),…,( xn , yn ) 的中心( ) B、若两个具有线性相关关系的变量的相关性越强,则线性相关系数r的值越接近于0 C、在残差图中,残差点分布的水平带状区域越窄,说明模型的拟合精度越高 D、在线性回归模型中,相关指数R2越接近于1,说明回归的效果越好6. 公元前四世纪,毕达哥拉斯学派对数和形的关系进行了研究.他们借助几何图形(或格点)来表示数,称为形数.形数是联系算术和几何的纽带.如图所示,数列1,6,15,28,45,…,从第二项起每一项都可以用六边形表示出来,故称它们为六边形数,那么该数列的第11项对应的六边形数为( )
 A、153 B、190 C、231 D、2767. 函数 的图象大致为 ( )A、
A、153 B、190 C、231 D、2767. 函数 的图象大致为 ( )A、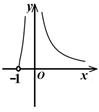 B、
B、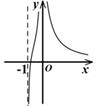 C、
C、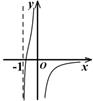 D、
D、 8. 曲线y=x2与直线y=x所围成的封闭图形的面积为( )A、1 B、 C、 D、9. 2020年6月23日,我国第55颗北斗导航卫星发射成功.为提升卫星健康运转的管理水平,西安卫星测控中心组织青年科技人员进行卫星监测技能竞赛,成绩分为“优秀”、“良好”、“待提高”三个等级.现有甲、乙、丙、丁四人参赛,已知这四人获得“优秀”的概率分别为 、 、 、 ,且四人是否获得“优秀”相互独立,则至少有 人获得“优秀”的概率为( )A、 B、 C、 D、10. 已知 ,c=e(e为自然对数的底数),则a、b、c的大小关系是( )A、a>b>c B、c>a>b C、c>b>a D、b>a>c11. 2020年4月30日,我国的5G信号首次覆盖了海拔8000米的珠穆朗玛峰峰顶和北坡登山路线,为了保证中国登山队珠峰高程测量的顺利直播,现从海拔5300米、5800米和6500米的三个大本营中抽出了4名技术人员,派往北坡登山路线中的3个崎岖路段进行信号检测,每个路段至少安排1名技术人员,则不同的安排方法共有( )A、72 B、36 C、48 D、5412. 若不等式ex﹣ax2﹣ ax>0对于任意的x∈R恒成立,则实数a的取值范围是( )A、( ,0] B、[0, ) C、(0, ) D、(﹣∞, )
8. 曲线y=x2与直线y=x所围成的封闭图形的面积为( )A、1 B、 C、 D、9. 2020年6月23日,我国第55颗北斗导航卫星发射成功.为提升卫星健康运转的管理水平,西安卫星测控中心组织青年科技人员进行卫星监测技能竞赛,成绩分为“优秀”、“良好”、“待提高”三个等级.现有甲、乙、丙、丁四人参赛,已知这四人获得“优秀”的概率分别为 、 、 、 ,且四人是否获得“优秀”相互独立,则至少有 人获得“优秀”的概率为( )A、 B、 C、 D、10. 已知 ,c=e(e为自然对数的底数),则a、b、c的大小关系是( )A、a>b>c B、c>a>b C、c>b>a D、b>a>c11. 2020年4月30日,我国的5G信号首次覆盖了海拔8000米的珠穆朗玛峰峰顶和北坡登山路线,为了保证中国登山队珠峰高程测量的顺利直播,现从海拔5300米、5800米和6500米的三个大本营中抽出了4名技术人员,派往北坡登山路线中的3个崎岖路段进行信号检测,每个路段至少安排1名技术人员,则不同的安排方法共有( )A、72 B、36 C、48 D、5412. 若不等式ex﹣ax2﹣ ax>0对于任意的x∈R恒成立,则实数a的取值范围是( )A、( ,0] B、[0, ) C、(0, ) D、(﹣∞, )二、填空题
-
13. 已知 ,且 ,则实数 的值为.14. 某种疾病的患病率为0.50,患该种疾病且血检呈阳性的概率为0.49,则已知在患该种疾病的条件下血检呈阳性的概率为.15. 某学校贯彻“科学防疫”,实行“佩戴口罩,间隔而坐” .一排8个座位,安排4名同学就坐,共有种不同的安排方法.(用数字作答)
三、双空题
-
16. 已知函数 ) , 若 ,则函数 有个零点;若函数 有 个零点,则实数 的取值范围是.
四、解答题
-
17. 为了做好中央提出的“六稳”工作,落实“六保”任务,努力实现全年经济社会发展目标,某省采取了“云”上谈生意助力经济加速发展的稳外贸措施,通过电商平台,为外贸企业“在线洽谈、直播营销”提供服务和支持.已知该省某电商平台为某外贸工厂的产品开设直播带货专场,为了对该产品进行合理定价,用不同的单价在平台试销,得到如表数据:
单价x(元/件)
8
8.2
8.4
8.6
8.8
9
销量y(万件)
90
84
83
80
75
68
参考公式:回归方程 , ,
(1)、根据以上数据,求y关于x的线性回归方程;(2)、现已知该产品成本是4元/件,假设该产品全部卖出,请预测把单价定为多少时,此外贸工厂可获得的利润最大?18. 2020年寒假是特殊的寒假,因为疫情全体学生只能在家进行网上在线学习,为了研究学生在网上学习的情况,某学校在网上随机抽取120名学生对线上教育进行调查,其中男生与女生的人数之比为11∶13,其中男生30人对于线上教育满意,女生中有15名表示对线上教育不满意.参考公式:附:
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
0.706
3.841
5.024
6.635
7.879
10828
(1)、完成 列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;满意
不满意
总计
男生
女生
合计
120
(2)、从被调查中对线上教育满意的学生中,利用分层抽样抽取8名学生,再在8名学生中抽取3名学生,作线上学习的经验介绍,其中抽取男生的个数为 ,求出 的分布列及期望值.19. 已知 ( ).(1)、当 时,求 的单调区间;(2)、令 ,若 在区间 上单调递减,求实数a的取值范围.20. 2020年4月,受新型冠状病毒疫情的影响,某校初三年级500名学生参加了市里组织的线上联考,这500名学生的数学成绩(满分120分)的频率分布直方图如图所示(用样本的频率作为概率). (1)、由频率分布直方图,可以认为学生成绩z服从正态分布N(μ,σ2),其中μ,σ2分别取考生的平均成绩 (同一组中的数据用该组区间的中点值作为代表)和考生成绩的方差S2 , 请估计该校500名学生的成绩不低于99.31分的人数(结果四舍五入取整数).(2)、现从该市参加线上联考的学生中随机抽取20名,设其中有k名学生的数学成绩在[100,120]内的概率为P(X=k)(k=0,1,2,…20),则当P(X=k)最大时,求k的值.
(1)、由频率分布直方图,可以认为学生成绩z服从正态分布N(μ,σ2),其中μ,σ2分别取考生的平均成绩 (同一组中的数据用该组区间的中点值作为代表)和考生成绩的方差S2 , 请估计该校500名学生的成绩不低于99.31分的人数(结果四舍五入取整数).(2)、现从该市参加线上联考的学生中随机抽取20名,设其中有k名学生的数学成绩在[100,120]内的概率为P(X=k)(k=0,1,2,…20),则当P(X=k)最大时,求k的值.附:①s2=28.2, ;②若z~N(μ,σ2),则P(μ﹣σ<z<μ+σ)≈0.6827,P(μ﹣2σ<z<μ+2σ)≈0.9545,P(μ﹣3σ<z<μ+3σ)≈0.9973.
-