重庆市四区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-08-21 类型:期末考试
一、选择题
-
1. 下列所叙述的图形中,全等的两个三角形是( )A、含有45°角的两个直角三角形 B、腰相等的两个等腰三角形 C、边长相等的两个等边三角形 D、一个钝角对应相等的两个等腰三角形2. 在平行四边形ABCD中,若∠B=135°,则∠D=( )A、45° B、55° C、135° D、145°3. 已知点P的坐标为(a,b)(a>0),点Q的坐标为(c,2),且|a-c|+ =0,将线段PQ向右平移a个单位长度,其扫过的面积为24,那么a+b+c的值为( )A、12 B、14 C、16 D、204. 如图,△ABC中,AC=BC,点P为AB上的动点(不与A,B重合)过P作PE⊥AC于E,PF⊥BC于F设AP的长度为x,PE与PF的长度和为y,则能表示y与x之间的函数关系的图象大致是( )
 A、
A、 B、
B、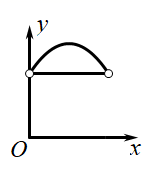 C、
C、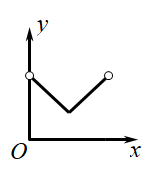 D、
D、 5. 一个容量为80的样本最大值为143,最小值为50,取组距为10,则可以分成( )A、10组 B、9组 C、8组 D、7组6. 如图,△ABC中,∠A=30°,∠ACB=90°,BC=2,D是AB上的动点,将线段CD绕点C逆时针旋转90°,得到线段CE,连接BE,则BE的最小值是( )
5. 一个容量为80的样本最大值为143,最小值为50,取组距为10,则可以分成( )A、10组 B、9组 C、8组 D、7组6. 如图,△ABC中,∠A=30°,∠ACB=90°,BC=2,D是AB上的动点,将线段CD绕点C逆时针旋转90°,得到线段CE,连接BE,则BE的最小值是( ) A、 -1 B、 C、 D、27. 如图,已知四边形ABCD是边长为4的正方形,E为CD上一点,且DE=1,F为射线BC上一动点,过点E作EG⊥AF于点P,交直线AB于点G.则下列结论中:①AF=EG;②若∠BAF=∠PCF,则PC=PE;③当∠CPF=45°时,BF=1;④PC的最小值为 ﹣2.其中正确的有( )
A、 -1 B、 C、 D、27. 如图,已知四边形ABCD是边长为4的正方形,E为CD上一点,且DE=1,F为射线BC上一动点,过点E作EG⊥AF于点P,交直线AB于点G.则下列结论中:①AF=EG;②若∠BAF=∠PCF,则PC=PE;③当∠CPF=45°时,BF=1;④PC的最小值为 ﹣2.其中正确的有( )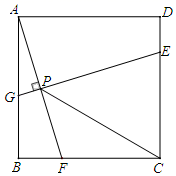 A、1个 B、2个 C、3个 D、4个8. 如图,已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(10,0),点B(0,6),点P为BC边上的动点,将△OBP沿OP折叠得到△OPD,连接CD、AD.则下列结论中:①当∠BOP=45°时,四边形OBPD为正方形;②当∠BOP=30°时,△OAD的面积为15;③当P在运动过程中,CD的最小值为2 ﹣6;④当OD⊥AD时,BP=2.其中结论正确的有( )
A、1个 B、2个 C、3个 D、4个8. 如图,已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(10,0),点B(0,6),点P为BC边上的动点,将△OBP沿OP折叠得到△OPD,连接CD、AD.则下列结论中:①当∠BOP=45°时,四边形OBPD为正方形;②当∠BOP=30°时,△OAD的面积为15;③当P在运动过程中,CD的最小值为2 ﹣6;④当OD⊥AD时,BP=2.其中结论正确的有( ) A、1个 B、2个 C、3个 D、4个9. 在边长为5的正方形ABCD中,以A为一个顶点,另外两个顶点在正方形ABCD的边上作等腰三角形,且含边长为4的所有大小不同的等腰三角形的个数为( )A、6 B、5 C、4 D、310. 如图,在Rt△DEF中,∠EFD=90°,∠DEF=30°,EF=3cm,边长为2cm的等边△ABC的顶点C与点E重合,另一个顶点B(在点C的左侧)在射线FE上.将△ABC沿EF方向进行平移,直到A、D、F在同一条直线上时停止,设△ABC在平移过程中与△DEF的重叠面积为ycm2 , CE的长为xcm,则下列图象中,能表示y与x的函数关系的图象大致是( )
A、1个 B、2个 C、3个 D、4个9. 在边长为5的正方形ABCD中,以A为一个顶点,另外两个顶点在正方形ABCD的边上作等腰三角形,且含边长为4的所有大小不同的等腰三角形的个数为( )A、6 B、5 C、4 D、310. 如图,在Rt△DEF中,∠EFD=90°,∠DEF=30°,EF=3cm,边长为2cm的等边△ABC的顶点C与点E重合,另一个顶点B(在点C的左侧)在射线FE上.将△ABC沿EF方向进行平移,直到A、D、F在同一条直线上时停止,设△ABC在平移过程中与△DEF的重叠面积为ycm2 , CE的长为xcm,则下列图象中,能表示y与x的函数关系的图象大致是( )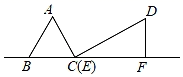 A、
A、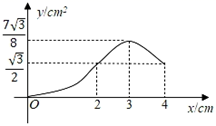 B、
B、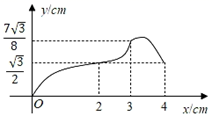 C、
C、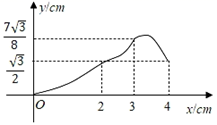 D、
D、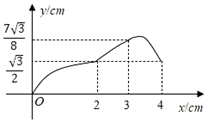 11. 若直线y=-2x-4与直线y=4x+b的交点在第三象限,则b的取值范围是( )A、-4<b<8 B、-4<b<0 C、b<-4或b>8 D、-4≤6≤812. 正比例函数 的图象上有两点 , ,则 与 的大小关系是( )A、 B、 C、 D、
11. 若直线y=-2x-4与直线y=4x+b的交点在第三象限,则b的取值范围是( )A、-4<b<8 B、-4<b<0 C、b<-4或b>8 D、-4≤6≤812. 正比例函数 的图象上有两点 , ,则 与 的大小关系是( )A、 B、 C、 D、二、填空题
-
13. 已知某汽车油箱中的剩余油量y(升)与该汽车行驶里程数x(千米)是一次函数关系,当汽车加满油后,行驶200千米,油箱中还剩油126升,行驶250千米,油箱中还剩油120升,那么当油箱中还剩油90升时,该汽车已行驶了千米14. 点 向平移2个单位后,所对应的点的坐标是 .15. 如图,∠XOY=45°,一把直角三角尺△ABC的两个顶点A、B分别在OX,OY上移动,其中AB=10,那么点O到顶点A的距离的最大值为.
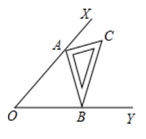 16. 如图,▱ABCD中,∠DAB=30°,AB=6,BC=2,P为边CD上的一动点,则2PB+ PD的最小值等于.
16. 如图,▱ABCD中,∠DAB=30°,AB=6,BC=2,P为边CD上的一动点,则2PB+ PD的最小值等于. 17. 如图,已知点A是第一象限内横坐标为 的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是.
17. 如图,已知点A是第一象限内横坐标为 的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是. 18. 小强调查“每人每天的用水量”这一问题时,收集到80个数据,最大数据是70升,最小数据是42升,若取组距为4,则应分为组绘制频数分布表.
18. 小强调查“每人每天的用水量”这一问题时,收集到80个数据,最大数据是70升,最小数据是42升,若取组距为4,则应分为组绘制频数分布表.三、解答题
-
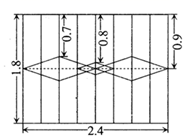
19. 根据下列条件求出相应的函数表达式:(1)、直线y=kx+5经过点(-2,-1);(2)、一次函数中,当x=1时,y=3;当x=-1时,y=7.20. 某工人为一客户制作一长方形防盗窗,为了牢固和美观,设计如图所示,中间为三个菱形,其中左右为两个全等的大菱形,中间为一个小菱形,竖着的铁棍的间距是相等的,尺寸如图所示(单位:m),工人师傅要做这样的一个防盗窗,总共需要多长的铁棍(不计损耗?)
 21. 如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.
21. 如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.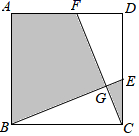 (1)、求 BGC的度数;(2)、若CE=1,H为BF的中点时,求HG的长度;(3)、若图中阴影部分的面积与正方形ABCD的面积之比为2:3,求△BCG的周长.22. 如图,在长方形 中,O为平面直角坐标系的原点,点 在x轴上,点 在y轴上,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着 的路线移动(即沿着长方形的边移动一周).
(1)、求 BGC的度数;(2)、若CE=1,H为BF的中点时,求HG的长度;(3)、若图中阴影部分的面积与正方形ABCD的面积之比为2:3,求△BCG的周长.22. 如图,在长方形 中,O为平面直角坐标系的原点,点 在x轴上,点 在y轴上,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着 的路线移动(即沿着长方形的边移动一周).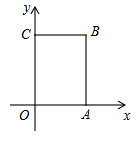 (1)、分别求出A,C两点的坐标;(2)、当点P移动了4秒时,求出点P的坐标;(3)、在移动过程中,当三角形 的面积是10时,求满足条件的点P的坐标及相应的点P移动的时间.23. 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系式.根据题中所给信息解答以下问题:
(1)、分别求出A,C两点的坐标;(2)、当点P移动了4秒时,求出点P的坐标;(3)、在移动过程中,当三角形 的面积是10时,求满足条件的点P的坐标及相应的点P移动的时间.23. 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系式.根据题中所给信息解答以下问题: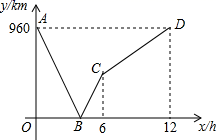 (1)、甲、乙两地之间的距离为km;图中点C的实际意义为:;慢车的速度为 , 快车的速度为;(2)、求线段BC所表示的y与x之间的函数关系式,以及自变量x的取值范围;(3)、若在第一列快车与慢车相遇时,第二列车从乙地出发驶往甲地,速度与第一列快车相同,请直接写出第二列快车出发多长时间,与慢车相距200km.24. 某校为了了解学生在校吃午餐所需时间的情况,抽查了20名同学在校吃午餐所花的时间,获得如下数据(单位:min):
(1)、甲、乙两地之间的距离为km;图中点C的实际意义为:;慢车的速度为 , 快车的速度为;(2)、求线段BC所表示的y与x之间的函数关系式,以及自变量x的取值范围;(3)、若在第一列快车与慢车相遇时,第二列车从乙地出发驶往甲地,速度与第一列快车相同,请直接写出第二列快车出发多长时间,与慢车相距200km.24. 某校为了了解学生在校吃午餐所需时间的情况,抽查了20名同学在校吃午餐所花的时间,获得如下数据(单位:min):10,12,15,10,16,18,19,18,20,38,
22,25,20,18,18,20,15,16,21,16.
(1)、若将这些数据分为6组,请列出频数表,画出频数直方图;(2)、根据频数直方图,你认为校方安排学生吃午餐时间多长为宜?请说明理由.25. 如图,在正方形ABCD中,E是CD边的中点,AC与BE相交于点F,连接DF.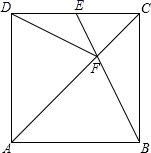 (1)、在不增加点和线的前提下,直接写出图中所有的全等三角形;(2)、连接AE,试判断AE与DF的位置关系,并证明你的结论;(3)、延长DF交BC于点M,试判断BM与MC的数量关系.(直接写出结论)26. 已知三角形ABC中,∠ACB=90°,点D(0,-4),M(4,-4).
(1)、在不增加点和线的前提下,直接写出图中所有的全等三角形;(2)、连接AE,试判断AE与DF的位置关系,并证明你的结论;(3)、延长DF交BC于点M,试判断BM与MC的数量关系.(直接写出结论)26. 已知三角形ABC中,∠ACB=90°,点D(0,-4),M(4,-4).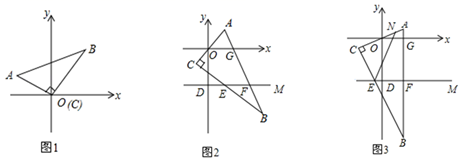 (1)、如图1,若点C与点O重合,A(-2,2)、B(4,4),求△ABC的面积;(2)、如图2,AC经过坐标原点O,点C在第三象限且点C在直线DM与x轴之间,AB分别与x轴,直线DM交于点G,F,BC交DM于点E,若∠AOG=55°,求∠CEF的度数;(3)、如图3,AC经过坐标原点O,点C在第三象限且点C在直线DM与x轴之间,N为AC上一点,AB分别与x轴,直线DM交于点G,F,BC交DM于点E,∠NEC+∠CEF=180°,求证∠NEF=2∠AOG.
(1)、如图1,若点C与点O重合,A(-2,2)、B(4,4),求△ABC的面积;(2)、如图2,AC经过坐标原点O,点C在第三象限且点C在直线DM与x轴之间,AB分别与x轴,直线DM交于点G,F,BC交DM于点E,若∠AOG=55°,求∠CEF的度数;(3)、如图3,AC经过坐标原点O,点C在第三象限且点C在直线DM与x轴之间,N为AC上一点,AB分别与x轴,直线DM交于点G,F,BC交DM于点E,∠NEC+∠CEF=180°,求证∠NEF=2∠AOG.