浙江省瑞安市2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-08-21 类型:期末考试
一、选择题
-
1. 使二次根式 有意义的x的取值范围是( )A、x≠2 B、x>2 C、x≤2 D、x≥22. 四边形的内角和为( )A、180° B、360° C、540° D、720°3. 下列选项中,计算正确的是( )A、 B、 C、 D、4. 用反证法证明“若 ,则 ”时应假设( )A、 B、 C、 D、5. 下列手机应用软件的图标中,属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 6. 用配方法解方程 ,下列配方正确的是( )A、 B、 C、 D、7. 在 中,若 ,则 的度数为( )A、 B、 C、 D、8. 某品牌运动服原来每件售价400元,受疫情影响经过连续两次降价后,现在每件售价为256元,设平均每次降价的百分率为x,根据题意可列方程( )A、 B、 C、 D、9. 已知反比例函数 ,当 时,y的最大值是4,则当 时,y有( )A、最小值-4 B、最小值-2 C、最大值-4 D、最大值-210. “勾股图”有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了以“勾股图”为背景的邮票(如图1),欧几里得在《几何原本》中曾对该图做了深入研究.如图2,在 中, ,分别以 的三条边为边向外作正方形,连结 , , , 分别与 , 相交于点P,Q.若 ,则 的值为( )
6. 用配方法解方程 ,下列配方正确的是( )A、 B、 C、 D、7. 在 中,若 ,则 的度数为( )A、 B、 C、 D、8. 某品牌运动服原来每件售价400元,受疫情影响经过连续两次降价后,现在每件售价为256元,设平均每次降价的百分率为x,根据题意可列方程( )A、 B、 C、 D、9. 已知反比例函数 ,当 时,y的最大值是4,则当 时,y有( )A、最小值-4 B、最小值-2 C、最大值-4 D、最大值-210. “勾股图”有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了以“勾股图”为背景的邮票(如图1),欧几里得在《几何原本》中曾对该图做了深入研究.如图2,在 中, ,分别以 的三条边为边向外作正方形,连结 , , , 分别与 , 相交于点P,Q.若 ,则 的值为( )
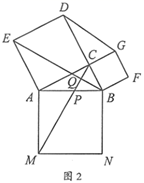 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
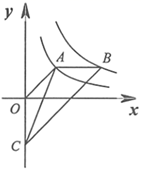
11. 当 时,二次根式 的值为.12. 甲、乙两人各进行10次射击比赛,平均成绩均为9环,方差分别是:S2甲 ,S2乙 ,则射击成绩较稳定的是(选填“甲”或“乙”).13. 若关于 的一元二次方程 有两个相等的实数根,则 的值是 .14. 若矩形中较短的边长为4,两对角线的夹角为 ,则矩形对角线的长是.15. 如图,已知点 在反比例函数 的图象上,过点A作x轴的平行线交反比例函数 的图象于点B,连结 ,过点B作 交y轴于点C,连结 ,则 的面积为.
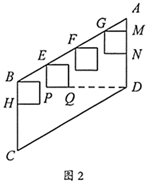
 16. 如图1,某学校楼梯墙面上悬挂了四幅全等的正方形画框,画框下边缘与水平地面平行.如图2,画框的左上角顶点B,E,F,G都在直线 上,且 ,楼梯装饰线条所在直线 ,延长画框的边 , 得到 .若直线 恰好经过点 , , , ,则正方形画框的边长为 .
16. 如图1,某学校楼梯墙面上悬挂了四幅全等的正方形画框,画框下边缘与水平地面平行.如图2,画框的左上角顶点B,E,F,G都在直线 上,且 ,楼梯装饰线条所在直线 ,延长画框的边 , 得到 .若直线 恰好经过点 , , , ,则正方形画框的边长为 .
三、解答题
-
17. 解下列方程:(1)、(2)、18. 已知(如图),在四边形ABCD中AB=CD,过A作AE⊥BD交BD于点E,过C作CF⊥BD交BD于F,且AE=CF.求证:四边形ABCD是平行四边形.
 19. 我们把每个顶点都在格点的四边形叫做格点四边形.如图,在所给的 方格纸中,点A,B均为格点,请画出符合要求的格点四边形.
19. 我们把每个顶点都在格点的四边形叫做格点四边形.如图,在所给的 方格纸中,点A,B均为格点,请画出符合要求的格点四边形.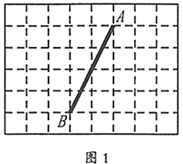
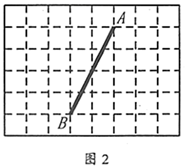 (1)、在图1中画出一个以 为边的矩形 ,且它的面积为整数;(2)、在图2中画出一个以 为对角线的菱形 ,且它的周长为整数.20. 某车间有工人15人,某月他们生产的零件个数统计如下表:
(1)、在图1中画出一个以 为边的矩形 ,且它的面积为整数;(2)、在图2中画出一个以 为对角线的菱形 ,且它的周长为整数.20. 某车间有工人15人,某月他们生产的零件个数统计如下表:生产零件的个数(个)
600
480
220
180
120
90
工人人数(人)
1
1
3
3
3
4
(1)、求这15名工人该月生产零件的平均个数;(2)、为了调动工人的积极性,决定实行目标管理,对完成目标的工人进行适当的奖励.如果想让一半左右的工人都能获得奖励,请你从平均数、中位数、众数的角度进行分析,该如何确定月生产目标?21. 如图,菱形 放置在平面直角坐标系中,已知点 , ,点D在y轴正半轴上,反比例函数的图象经过点C.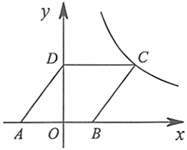 (1)、求反比例函数的表达式;(2)、将菱形 向上平移,使点 恰好落在双曲线上,此时A,B,C,D的对应点分别为 , , , ,且 与双曲线交于点 ,求点 的坐标.22. 某商店销售一款口罩,每袋的进价为12元.经市场调查发现,每袋售价每增加1元,日均销售量减少5袋.当售价为每袋18元时,日均销售量为100袋.设口罩每袋的售价为x元,日均销售量为y袋.(1)、用含x的代数式表示y;(2)、物价部门规定,该款口罩的每袋售价不得高于22元.当每袋售价定为多少元时,商店销售该款口罩所得的日均毛利润为720元?23. 如图,正方形 的边长为6.E,F分别是射线 , 上的点(不与点A重合),且 ,M为 的中点.P为线段 上一点, ,连结 .
(1)、求反比例函数的表达式;(2)、将菱形 向上平移,使点 恰好落在双曲线上,此时A,B,C,D的对应点分别为 , , , ,且 与双曲线交于点 ,求点 的坐标.22. 某商店销售一款口罩,每袋的进价为12元.经市场调查发现,每袋售价每增加1元,日均销售量减少5袋.当售价为每袋18元时,日均销售量为100袋.设口罩每袋的售价为x元,日均销售量为y袋.(1)、用含x的代数式表示y;(2)、物价部门规定,该款口罩的每袋售价不得高于22元.当每袋售价定为多少元时,商店销售该款口罩所得的日均毛利润为720元?23. 如图,正方形 的边长为6.E,F分别是射线 , 上的点(不与点A重合),且 ,M为 的中点.P为线段 上一点, ,连结 .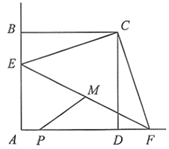 (1)、求证: ;(2)、当 为直角三角形时,求 的长;(3)、记 边的中点为N,连结 ,若 ,则 的面积为.(在横线上直接写出答案)
(1)、求证: ;(2)、当 为直角三角形时,求 的长;(3)、记 边的中点为N,连结 ,若 ,则 的面积为.(在横线上直接写出答案)