浙江省宁波市镇海区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-08-21 类型:期末考试
一、选择题
-
1. 要使代数式 有意义,x的取值范围满足( )A、 B、x≠2 C、x>2 D、x<22. 随着人民生活水平的不断提高,汽车逐渐成为了很多家庭的必需品.下列四个汽车标志中,既是中心对称图形,又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )A、6 B、7 C、8 D、94. 已知四边形ABCD中AC=BD,再补充一个条件使得四边形ABCD是矩形,这个条件可以是( )A、AC⊥BD B、∠ABC=90° C、AC与BD互相平分 D、AB=BC5. 在全国人民的共同努力下,新冠肺炎确诊病例逐渐减少,据统计,某地区2月份新冠肺炎确诊病例144例,4月份新冠肺炎确诊病例36例,设这两个月确诊病例平均每月降低的百分率是x,则下列关于x的方程正确的是( )A、 B、 C、 D、6. 用反证法证明“四边形中至少有一个内角大于或等于90°”时,应先假设( )A、有一个内角小于90° B、每一个内角都大于90° C、有一个内角小于或等于90° D、每一个内角都小于90°7. 若关于x的一元二次方程 有两个不相等的实数根,则实数k的取值范围是( )A、 B、 C、 D、8. 如图,在平行四边形 中,对角线 , 交于点O, ,点 ,F,G分别是 , , 的中点, 交 于点H,下列4个结论中说法正确的有( )
3. 如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )A、6 B、7 C、8 D、94. 已知四边形ABCD中AC=BD,再补充一个条件使得四边形ABCD是矩形,这个条件可以是( )A、AC⊥BD B、∠ABC=90° C、AC与BD互相平分 D、AB=BC5. 在全国人民的共同努力下,新冠肺炎确诊病例逐渐减少,据统计,某地区2月份新冠肺炎确诊病例144例,4月份新冠肺炎确诊病例36例,设这两个月确诊病例平均每月降低的百分率是x,则下列关于x的方程正确的是( )A、 B、 C、 D、6. 用反证法证明“四边形中至少有一个内角大于或等于90°”时,应先假设( )A、有一个内角小于90° B、每一个内角都大于90° C、有一个内角小于或等于90° D、每一个内角都小于90°7. 若关于x的一元二次方程 有两个不相等的实数根,则实数k的取值范围是( )A、 B、 C、 D、8. 如图,在平行四边形 中,对角线 , 交于点O, ,点 ,F,G分别是 , , 的中点, 交 于点H,下列4个结论中说法正确的有( )① ;② ;③ ;④ .
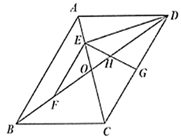 A、①② B、①②③ C、①③④ D、①②③④9. 如图,已知正方形的边长为2,点E是正方形 的边 上的一点,点A关于的对称点为F,若 ,则的长为( )
A、①② B、①②③ C、①③④ D、①②③④9. 如图,已知正方形的边长为2,点E是正方形 的边 上的一点,点A关于的对称点为F,若 ,则的长为( )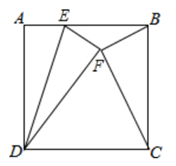 A、 B、 C、 D、10. 矩形 内放入两张边长分别为 和 的正方纸片,按照图①放置,矩形纸片没有两个正方形覆盖的部分(黑色阴影部分)的面积为 ;按照图②放置,矩形纸片没有被两个正方形覆盖的部分面积为 ;按图③放置,矩形纸片没有被两个正方形覆盖的部分的面积为 .已知 , ,设 ,则下列值是常数的是( )
A、 B、 C、 D、10. 矩形 内放入两张边长分别为 和 的正方纸片,按照图①放置,矩形纸片没有两个正方形覆盖的部分(黑色阴影部分)的面积为 ;按照图②放置,矩形纸片没有被两个正方形覆盖的部分面积为 ;按图③放置,矩形纸片没有被两个正方形覆盖的部分的面积为 .已知 , ,设 ,则下列值是常数的是( )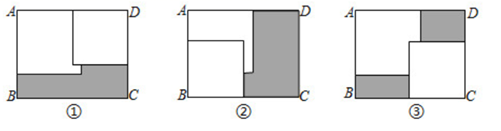 A、 B、 C、 D、a+b
A、 B、 C、 D、a+b二、填空题
-
11. 比较大小: (填“>”或“<”或“=”).12. 已知一组数据:1,3,5,5,6,则这组数据的方差是.13. 已知 是关 的方程 的一个根,则 .14. 如图,AD是正五边形ABCDE的一条对角线,则∠BAD=°.
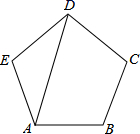 15. 如图,菱形 的边长是4, ,点E,F分别是 , 边上的动点(不与点A,B,C重合),且 ,若 , , 与 相交于点G,当 为等腰三角形时, 的长为.
15. 如图,菱形 的边长是4, ,点E,F分别是 , 边上的动点(不与点A,B,C重合),且 ,若 , , 与 相交于点G,当 为等腰三角形时, 的长为.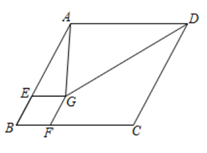 16. 如图,正方形 的边长为6,E是边 的中点,F是边 上的一个动点, ,且 ,则 的最小值为.
16. 如图,正方形 的边长为6,E是边 的中点,F是边 上的一个动点, ,且 ,则 的最小值为.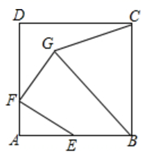
三、解答题
-
17. 计算:(1)、(2)、18. 解下列方程:(1)、(2)、19. 如图,坐标平面内的网格中,每个小正方形的边长均为1个单位, 的三个顶点在图中相应的格点上,点 的坐标为 .
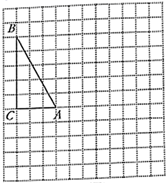
( 1 )请在网格平面内作出平面直角坐标系;
( 2 )作出与 关于原点对称的图形 ;
( 3 )请直接写出:以 , , , 为顶点的平行四边形的第四个顶点 的坐标(写出所有情况).
20. 停课不停学,疫情期间,八(1)班30位同学参加运动线上打卡,张老师为了鼓励同学们积极锻炼,统计了这30人15天的打卡次数如下:打卡次数
7
8
9
14
15
人数
6
9
6
3
6
(1)、直接写出打卡次数的众数和中位数;(2)、求所有同学打卡次数的平均数;(3)、为了调动同学们锻炼的积极性,张老师决定制定一个打卡奖励标准,凡打卡次数达到或超过这个标准的同学将获得奖励,请你根据(1)、(2)中所求的统计量,帮助张老师制定一个较为合理的打卡奖励标准,并说明理由.21. 如图,平行四边形 的对角线交于点O,以 , 为邻边作平行四边形 , 交 于点F,连结 .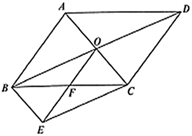 (1)、求证:F为 中点;(2)、若 , ,求平行四边形 的周长.22. 自2020年年初以来,全国多地猪肉价格连续上涨,引起了民众与政府的高度关注,政府向市场投入储备猪肉进行了价格平抑.据统计:某超市2020年1月10日这天猪肉售价为每千克56元,比去年同一天上涨了40%.(1)、求2019年1月10日,该超市猪肉的售价为每千克多少元?(2)、现在某超市以每千克46元的价格购进猪肉,按2020年月10日价格出售,平均一天能销售100千克.为促进消费,超市决定对这批猪肉进行降价销售,经调查表明:猪肉的售价每千克下降1元,平均每日销售量就增加18千克.为了实现平均每天有950元的销售利润,超市应将每千克猪肉定为多少元?23. 如图1,在平面直角坐标系中,直 分别交x,y轴于B,A两点,将 沿直线 折叠,使点B落在y轴上的点C处.
(1)、求证:F为 中点;(2)、若 , ,求平行四边形 的周长.22. 自2020年年初以来,全国多地猪肉价格连续上涨,引起了民众与政府的高度关注,政府向市场投入储备猪肉进行了价格平抑.据统计:某超市2020年1月10日这天猪肉售价为每千克56元,比去年同一天上涨了40%.(1)、求2019年1月10日,该超市猪肉的售价为每千克多少元?(2)、现在某超市以每千克46元的价格购进猪肉,按2020年月10日价格出售,平均一天能销售100千克.为促进消费,超市决定对这批猪肉进行降价销售,经调查表明:猪肉的售价每千克下降1元,平均每日销售量就增加18千克.为了实现平均每天有950元的销售利润,超市应将每千克猪肉定为多少元?23. 如图1,在平面直角坐标系中,直 分别交x,y轴于B,A两点,将 沿直线 折叠,使点B落在y轴上的点C处.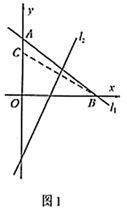
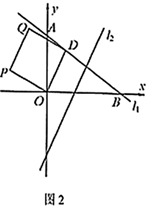
 (1)、①点A的坐标为 , 点B的坐标为;
(1)、①点A的坐标为 , 点B的坐标为;②求点C的坐标;
(2)、①点 在线段 上,当 与 面积相等时,求 所在直线的解析式;②如图2,在①的条件下,以 为一边作正方形 (点 在第二象限),求点 的坐标。
(3)、在射线 上是否还存在其它的点 ,使得 与 面积相等?若存在,求出点 的坐标;若不存在,请说明理由.24. 我们规定:有一组邻边相等,且这组邻边的夹角为 的凸四边形叫做“准筝形”.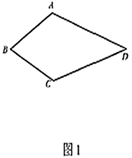
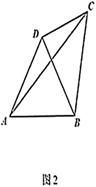
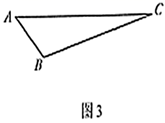
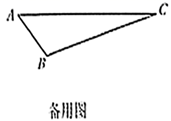 (1)、如图1,在四边形 中, , , ,求证:四边形 是“准筝形”;(2)、如图2,在“准筝形” 中, , , , ,求 的长;(3)、如图3,在 中, , , ,设 是 所在平面内一点,当四边形 是“准筝形”时,请直接写出四边形 的面积.
(1)、如图1,在四边形 中, , , ,求证:四边形 是“准筝形”;(2)、如图2,在“准筝形” 中, , , , ,求 的长;(3)、如图3,在 中, , , ,设 是 所在平面内一点,当四边形 是“准筝形”时,请直接写出四边形 的面积.