浙江省宁波市奉化区2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2020-08-21 类型：期末考试

进入出卷网下载

一、选择题

1. 下列图形中，既是轴对称图形又是中心对称图形的有（）

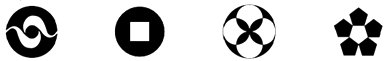A、4个 B、3个 C、2个 D、1个

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{{(- 3)}^{2}} = - 3$ B、 ${(2 \sqrt{3})}^{2} = 6$ C、 $\sqrt{2} + \sqrt{5} = \sqrt{7}$ D、 $\sqrt{2} \times \sqrt{5} = \sqrt{10}$

查看试题解析
3. 某篮球队12名队员的年龄如下表所示，则这12名队员年龄的众数和平均数是（）

年龄/岁

18

19

20

21

人数

5

4

1

2

A、19，19.5 B、19，19 C、18，19.5 D、18，19

查看试题解析
4. 矩形具有而一般平行四边形不具有的性质是（）

A、对角相等 B、对角线相等 C、对角线互相平分 D、对角线互相垂直

查看试题解析
5. 反证法证明“三角形中至少有一个角不小于60°”先应假设这个三角形中（　　）

A、有一个内角小于60° B、每个内角都小于60° C、有一个内角大于60° D、每个内角都大于60°

查看试题解析
6. 已知反比例函数y＝﹣ $\frac{2}{x}$ 的图象上有两点A（x₁ ， y₁），B（x₂ ， y₂），且x₁＜x₂＜0，则y₁ ， y₂的大小关系为（）

A、y₁＜y₂ B、y₁＞y₂ C、y₁＝y₂ D、无法确定

查看试题解析
7. 如图，在▱ABCD中，对角线AC与BD相交于点O，E是边CD的中点，连接OE，若∠COE＝35°，∠ADC＝45°，则∠BAC＝（）

A、70° B、90° C、100° D、110°

查看试题解析
8. 某班学生毕业时，都将自己的照片向本班其他同学送一张留念，全班一共送了1260张，如果全班有x名同学，根据题意，列出方程为（）

A、x（x+1）＝1260 B、2x（x+1）＝1260 C、x（x﹣1）＝1260 D、x（x﹣1）＝1260×2

查看试题解析
9. 如图，正方形ABCD边长为4，边BC上有一点E，以DE为边作矩形EDFG，使FG过点A，则矩形EDFG的面积是（）

A、16 $\sqrt{2}$ B、8 $\sqrt{2}$ C、8 $\sqrt{3}$ D、16

查看试题解析
10. 如图，在平面直角坐标系中，直线y＝﹣ $\frac{1}{2}$ x+1分别交x轴，y轴于点A，B，交反比例函数y₁＝ $\frac{2 k}{x}$ （k＜0，x＜0），y₂＝ $\frac{k}{x}$ （k＜0，x＞0）于点C，D两点，连接OC，OD，过点D作DE⊥x轴于点E，若△ODE的面积与△OCB的面积相等，则k的值是（）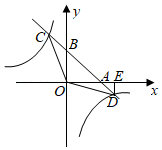

A、﹣4 B、﹣2 C、﹣2 $\sqrt{3}$ D、﹣ $\sqrt{5}$

查看试题解析

二、填空题

11. 若根式 $\sqrt{x - 2020}$ 有意义，则x的取值范围是.

查看试题解析
12. 若n边形的每一个外角都是72°，则边数n为.

查看试题解析
13. 一组数据1，3，2，5，x的平均数为3，那么这组数据的中位数是.

查看试题解析
14. 已知关于x的一元二次方程（m﹣2）x²+2x+1＝0有实数根，则m的取值范围是.

查看试题解析
15. 我国古代伟大的数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的直角三角形，得到一个恒等式，后人借助这种分割方法所得的图形证明了勾股定理.如图所示的矩形由两个这样的图形拼成，若a＝2，b＝3，则该矩形的面积为.

查看试题解析
16. 如图，在菱形纸片ABCD中，AB＝3，∠A＝60°，将菱形纸片翻折，使点A落在CD的中点E处，折痕为FG，点F，G分别在边AB，AD上，则EF的长为.

查看试题解析

三、解答题

17. 计算：

(1)、 $(\sqrt{24} - \sqrt{6}) \div \sqrt{2}$

(2)、 $(\sqrt{3} + 2) (\sqrt{3} - 2) + \sqrt{{(1 - \sqrt{3})}^{2}}$

查看试题解析
18. 解下列方程：

(1)、3（5﹣x）²＝2（x﹣5）；

(2)、x²﹣4x+2＝0.

查看试题解析
19. 为了参加“荆州市中小学生首届诗词大会”，某校八年级的两班学生进行了预选，其中班上前5名学生的成绩（百分制）分别为：八（1）班86，85，77，92，85；八（2）班79，85，92，85，89．通过数据分析，列表如下：
班级
平均分
中位数
众数
方差
八（1）
85
b
c
22.8
八（2）
a
85
85
19.2

(1)、直接写出表中a，b，c的值；

(2)、根据以上数据分析，你认为哪个班前5名同学的成绩较好？说明理由．

查看试题解析
20. 已知：关于x的方程 $x^{2} - (k + 2) x + 2 k = 0$ ，

(1)、求证：无论k取任何实数值，方程总有实数根；

(2)、若等腰三角形ABC的一边长a=1，两个边长b，c恰好是这个方程的两个根，求△ABC的周长．

查看试题解析
21. 如图，在菱形ABCD中，对角线AC，BD相交于点O，E是CD的中点，连接OE.过点C作CF//BD交OE的延长线于点F，连接DF.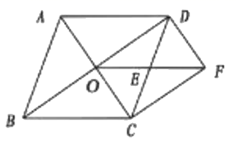

求证：

(1)、△ODE≌△FCE；

(2)、四边形OCFD是矩形。

查看试题解析
22. 如图，一次函数y₁＝kx+b的图象交坐标轴于A，C两点，交反比例函数y₂＝ $\frac{m}{x}$ 的图象于C，D两点，A（﹣2，0），C（1，3）.

(1)、分别求出一次函数和反比例函数的表达式.

(2)、求△COD的面积.

(3)、观察图象，直接写出y₁≥y₂时x的取值范围.

查看试题解析
23. 2020年突如其来的新型冠状病毒疫情，给生鲜电商带来了意想不到的流量和机遇，据统计某生鲜电商平台1月份的销售额是1440万元，3月份的销售额是2250万元.

(1)、若该平台1月份到3月份的月平均增长率都相同，求月平均增长率是多少？

(2)、市场调查发现，某水果在“盒马鲜生”平台上的售价为20元/千克时，每天能销售200千克，售价每降价2元，每天可多售出100千克，为了推广宣传，商家决定降价促销，同时尽量减少库存，已知该水果的成本价为12元/千克，若使销售该水果每天获利1750元，则售价应降低多少元？

查看试题解析
24. 定义：有一组邻边垂直且对角线相等的四边形为垂等四边形.

(1)、写出一个已学的特殊平行四边形中是垂等四边形的是.

(2)、如图1，在3×3方格纸中，A，B，C在格点上，请画出两个符合条件的不全等的垂等四边形，使AC，BD是对角线，点D在格点上.

(3)、如图2，在正方形ABCD中，点E，F，G分别在AD，AB，BC上，AE＝AF＝CG且∠DGC＝∠DEG，求证：四边形DEFG是垂等四边形.

(4)、如图3，已知Rt△ABC，∠B＝90°，∠C＝30°，AB＝2，以AC为边在AC的右上方作等腰三角形，使四边形ABCD是垂等四边形，请直接写出四边形ABCD的面积.

查看试题解析

班级	平均分	中位数	众数	方差
八（1）	85	b	c	22.8
八（2）	a	85	85	19.2

年龄/岁	18	19	20	21
人数	5	4	1	2