浙江省嘉兴市2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-08-21 类型:期末考试
一、选择题
-
1. 下列属于一元二次方程的是( )A、x2-3x+y=0 B、x2+2x= C、2x2=5x D、x(x2-4x)=32. 以下关于新型冠状病毒(2019-nCoV)的防范宣传图标中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
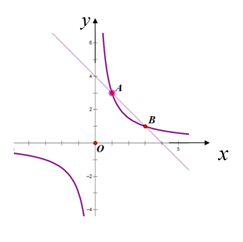
D、 3. 已知反比例函数的图象经过点(1,3),则这个反比例函数的表达式为( )A、y= B、y= C、y= D、y=-4. 下列各数中,能使二次根式 有意义的是( )A、-1 B、0 C、2 D、15. 如图,点E是▱ABCD中边BC延长线上一点,下列结论不一定成立的是( )
3. 已知反比例函数的图象经过点(1,3),则这个反比例函数的表达式为( )A、y= B、y= C、y= D、y=-4. 下列各数中,能使二次根式 有意义的是( )A、-1 B、0 C、2 D、15. 如图,点E是▱ABCD中边BC延长线上一点,下列结论不一定成立的是( )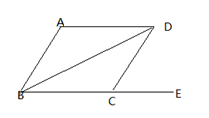 A、AB=CD B、∠ABD+∠ADB=∠DCE C、∠BAD=∠BCD D、∠ABD=∠CBD6. 已知一组数据x1 , x2 , x3 , 把每个数据都减去2,得到一组新数据x1-2,x2-2,x3-2,对比这两组数据的统计量不变的是( )A、平均数 B、方差 C、中位数 D、众数7. 用反证法证明命题“在四边形中至少有一个内角不大于90°”时,首先应假设( )A、每个内角都小于90° B、每个内角都大于90° C、没有一个内角大于90° D、每个内角都等于90°8. 点A(a,b),B(a-1,c)在反比例函数 的图象上,且 ,则b与c的大小关系为( )A、b<c B、b=c C、b>c D、不能确定9. 如图,在正方形ABCD中,点G为CD边上一点,以CG为边向右作正方形CEFG,连结AF,BD交于点P,连结BG,过点F作FH∥BG交BC于点H,连结AH,交BD于点K,下列结论中错误的是( )
A、AB=CD B、∠ABD+∠ADB=∠DCE C、∠BAD=∠BCD D、∠ABD=∠CBD6. 已知一组数据x1 , x2 , x3 , 把每个数据都减去2,得到一组新数据x1-2,x2-2,x3-2,对比这两组数据的统计量不变的是( )A、平均数 B、方差 C、中位数 D、众数7. 用反证法证明命题“在四边形中至少有一个内角不大于90°”时,首先应假设( )A、每个内角都小于90° B、每个内角都大于90° C、没有一个内角大于90° D、每个内角都等于90°8. 点A(a,b),B(a-1,c)在反比例函数 的图象上,且 ,则b与c的大小关系为( )A、b<c B、b=c C、b>c D、不能确定9. 如图,在正方形ABCD中,点G为CD边上一点,以CG为边向右作正方形CEFG,连结AF,BD交于点P,连结BG,过点F作FH∥BG交BC于点H,连结AH,交BD于点K,下列结论中错误的是( ) A、HE=CD B、△AHF是等腰直角三角形 C、点P为AF中点 D、PK=BK+DP10. 关于x的方程 (k为常数),下列说法:
A、HE=CD B、△AHF是等腰直角三角形 C、点P为AF中点 D、PK=BK+DP10. 关于x的方程 (k为常数),下列说法:①当k=1时,该方程的实数根为x=2;②x=1是该方程的实数根;③该方程有两个不相等的实数根.
其中正确的是( )
A、①② B、②③ C、② D、③二、填空题
-
11. 化简 =.12. 五边形的外角和等于°.13. 一元二次方程x2=2x的解为.14. 要使矩形ABCD成为正方形,可添加的条件是(写一个即可).15. 小丽参加单位举行的演讲比赛,评分规则及小丽的得分如下表:
演讲内容
语言表达
仪表仪容
所占比例
30%
60%
10%
小丽得分
90
85
75
则小丽的最终演讲评分为.
16. 已知反比例函数y= ,当x>3时,y的取值范围是 .17. 某商店4月份营业额为2.7万元,6月份营业额为3.5万元,平均每月的增长率为 ,根据题意可列方程为.18. 已知关于 的方程 (m是正整数)有实数根,则代数式 的值是.19. 如图,四边形ABCD中,AB=BC=3,∠A=∠C=90°,∠ABC=120°,点E是对角线BD上的一个动点,过点E分别作AB,BC,CD,AD的垂线,垂足分别为点F,H,I,G,连结FG和HI,则FG+HI的最小值为.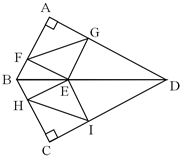 20. 如图,在平面直角坐标系xOy中,已知菱形ABCD的顶点A(0,2 )和C(2,0),顶点B在x轴上,顶点D在反比例函数y= 的图象上,点E为边CD上的动点,过点E作EF∥x轴交反比例函数图象于点F,过点F作FG∥CD交x轴于点G,当CE=CG时,点F的坐标为.
20. 如图,在平面直角坐标系xOy中,已知菱形ABCD的顶点A(0,2 )和C(2,0),顶点B在x轴上,顶点D在反比例函数y= 的图象上,点E为边CD上的动点,过点E作EF∥x轴交反比例函数图象于点F,过点F作FG∥CD交x轴于点G,当CE=CG时,点F的坐标为.
三、解答题
-
21. 计算:(1)、 -(2)、解方程:x²+4x-5=022. 如图,两张完全相同的方格纸,方格纸中的每个小正方形的边长均为1,A,B两点都在格点上,连结AB,请完成下列作图:
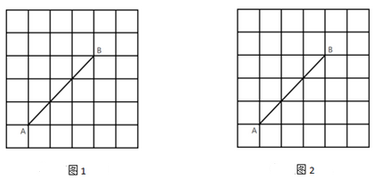 (1)、在图1中以AB为边作一个▱ABCD,使▱ABCD各顶点都在格点上.(2)、在图2中以AB为对角线作一个菱形,使得菱形的面积为15,且菱形各顶点都在格点上.23. 某校为了了解学生对“防溺水”安全知识的掌握情况,从各年级学生中抽取部分学生进行检测,并对所有抽测学生的成绩(百分制)进行统计得到如下表格,根据表格提供的信息解答下列问题:
(1)、在图1中以AB为边作一个▱ABCD,使▱ABCD各顶点都在格点上.(2)、在图2中以AB为对角线作一个菱形,使得菱形的面积为15,且菱形各顶点都在格点上.23. 某校为了了解学生对“防溺水”安全知识的掌握情况,从各年级学生中抽取部分学生进行检测,并对所有抽测学生的成绩(百分制)进行统计得到如下表格,根据表格提供的信息解答下列问题:某校部分学生“防溺水”安全知识检测成绩统计表
检测成绩分数段(分)
频数
频率
熟悉程度
90≤x≤100
24
0.48
非常熟悉
80≤x<90
a
0.36
熟悉
70≤x<80
6
0.12
有点熟悉
60≤x<70
2
b
不熟悉
(1)、求表中a和b的值(2)、分别写出抽测学生成绩中的中位数和众数所在的分数段(3)、如果该校有2600名学生,请估计本校对“防溺水”安全知识“非常熟悉”的学生人数24. 某一皮衣专卖店销售某款皮衣,其进价为每件750元,经市场调查发现,按每件1100元出售,平均每天可售出30件,每件降价50元,平均每天的销售量可增加10件,皮衣专卖店若想要平均每天获利12000元,则每件皮衣定价为多少元?(1)、以下是小明和小红的两种不同设法,请帮忙填完整小明:设每件皮衣降价x元,由题意,可列方程:.
小红:设每件皮衣定价为y元,由题意,可列方程:.
(2)、请写出一种完整的解答过程