浙江省杭州市下城区2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2020-08-21 类型：期末考试

进入出卷网下载

一、选择题

1. 下列图形是中心对称图形的是（）

A、等腰三角形 B、直角三角形 C、四边形 D、平行四边形

查看试题解析
2. 二次根式 $\sqrt{3 - a}$ ，则a的取值范围是（）

A、 $a$ ≤3 B、 $a$ ≤－3 C、 $a$ ＞3 D、 $a$ ＜3

查看试题解析
3. 正十二边形的一个内角的度数为（）

A、30° B、150° C、360° D、1800°

查看试题解析
4. 下列各式中正确的是（）

A、 $\sqrt{36}$ ＝±6 B、 $\sqrt{{(- 2)}^{- 2}} = - 2$ C、 $\sqrt{8}$ ＝4 D、 ${(- \sqrt{7})}^{2}$ ＝7

查看试题解析
5. 甲、乙两人在2020年上半年每月电费支出情况的统计图如图所示，则他们在2020年上半年月电费支出的方差S²甲和S²乙的大小关系是（）

A、 $S_{甲}^{2}$ ＜ $S_{乙}^{2}$ B、 $S_{甲}^{2}$ ＝ $S_{乙}^{2}$ C、 $S_{甲}^{2}$ ＞ $S_{乙}^{2}$ D、无法确定

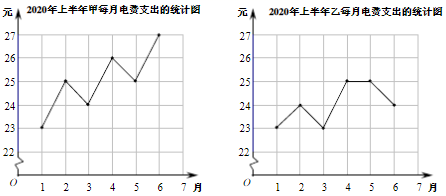查看试题解析
6. 假设命题“ $\sqrt{a^{2}}$ ＝a”不成立，则a与0的大小关系是（）

A、a＜0 B、a≤0 C、a≠0 D、a＞0

查看试题解析
7. 如图，四边形ABCD的对角线AC，BD交于点O，则不能判断四边形ABCD是平行四边形的是（）

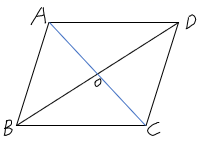A、∠ABD＝∠BDC，OA＝OC B、∠ABC＝∠ADC，AB＝CD C、∠ABC＝∠ADC，AD∥BC D、∠ABD＝∠BDC，∠BAD＝∠DCB

查看试题解析
8. 天猫某店铺第2季度的总销售额为331万元，其中4月份的销售额是100万元，设5，6月份的平均月增长率为x，则可列方程为（）

A、100（1＋x）²＝331 B、100＋100（1＋x）²＝331 C、100＋100（1＋x）＋100（1＋x）²＝331 D、100＋100x＋100（1＋x）²＝331

查看试题解析
9. 若 $\sqrt{{(a - b)}^{2}} = - a - b$ 则（）

A、 $| a + b | = 0$ B、 $| a - b | = 0$ C、 $| a b | = 0$ D、 $| a^{2} + b^{2} | = 0$

查看试题解析
10. 如图，在平行四边形ABCD中，点O是对角线BD的中点，过点O作线段EF，使点E点F分别在边AD，BC上（不与四边形ABCD顶点重合），连结EB，EC设ED＝kAE，下列结论：①若k＝1，则BE＝CE；②若k＝2，则△EFC与△OBE面积相等：③若△ABE≌△FEC，则EF⊥BD.其中正确的是（）

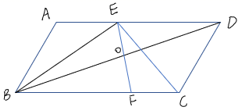A、① B、② C、③ D、②③

查看试题解析

二、填空题

11. 计算： $\sqrt{3} \times \sqrt{6} - \sqrt{2} =$ .

查看试题解析
12. 一元二次方程（x－ $\sqrt{5}$ ）（x＋ $\sqrt{5}$ ）＋（x－2）²＝0化为一般形式是.

查看试题解析
13. 若点A(1，－2)、B(－2，a)在同一个反比例函数的图象上，则a的值为.

查看试题解析
14. 如图，△ABC中，∠ACB＝90°，点M，N分别是AB，BC的中点，若CN＝2，CM＝ $\sqrt{5}$ ，则△ABC的周长.

查看试题解析
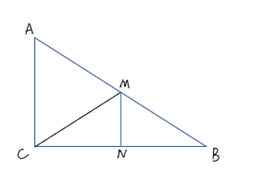15. 如图，把矩形纸片ABCD（BC＞CD）沿折痕DE折叠，点C落在对角线BD上的点P处：展开后再沿折痕BF折叠，点C落在BD上的点Q处：沿折痕DG折叠，点A落在BD上的点R处，若PQ＝4，PR＝7，则BD＝.

查看试题解析
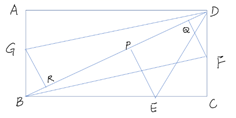16. 若反比例函数y＝ $\frac{4}{x}$ ，当x $\geq$ a或x $\leq -$ a时，函数值y范围内的整数有k个；当x $\geq$ a＋1或x $\leq$ －a－1时，函数值y范围内的整数有k－2个，则正整数a＝.

查看试题解析

三、解答题

17. 已知一元二次方程2x²－4x＋1＝0.

(1)、解这个方程；

(2)、设x₁和x₂是该方程的两个根，且x₁＞x₂ ，求2x₁－2x₂的值.

查看试题解析
18. 为了了解八年级学生的课外阅读情况，学校随机调查了该年级部分学生在一周内的课外阅读时间，绘制成如下统计表根据表中信息，回答下列问题：
八年级学生一周内的课外阅读时间统计表

时间（小时）

1

2

3

4

5

人数

12

17

13

5

3

(1)、求被抽查学生在一周内的课外阅读时间的平均数，并直接写出中位数和众数

(2)、若该校共有300名八年级学生，请你估算该校一周内课外阅读时间不少于3小时的学生人数？

查看试题解析
19. 如图，正方形ABCD边长为8，E，F分别是BC，CD上的点，且AE⊥BF.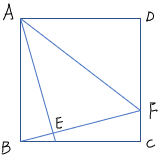

(1)、求证：AE＝BF；

(2)、若AF＝10，求AE的长.

查看试题解析
20. 小张准备进行如下实验操作：把一根长为20cm的铁丝剪成两段，并以每一段铁丝的长度为周长各做成一个正方形.

(1)、要使这两个正方形的面积之和等于13cm²则这两个正方形的边长是多少？

(2)、小张认为，这两个正方形的面积之和不可能等于11cm²你认为他的说法正确吗？请说明理由.

查看试题解析
21. 如图，平行四边形ABCD中，对角线AC，BD相交于点O，AE⊥BD于点E，DF⊥AC于点F，且AE＝DF.

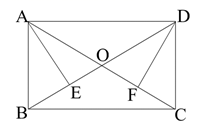(1)、求证：四边形ABCD是矩形；

(2)、若∠BAE∶∠EAD＝2∶3，求∠EAO的度数.

查看试题解析
22. 已知点M，P是反比例函数y＝ $\frac{k}{x}$ （k＞0）图象上两点，过点M作MN⊥x轴，过点P作PQ⊥x轴，垂足分别为点N，Q.若PQ＝ $\frac{1}{2}$ MN

(1)、若点P在第一象限内，点M坐标为(1，2)，求P的坐标；

(2)、若S_△_MNP＝2，求k的值；

(3)、设点M(1－2n，y₁)、P(2n＋1，y₂)，且y₁＜y₂ ，求n的范围.

查看试题解析
23. 如图，在△ABC中，AB＝AC，延长中线AD到点E，作∠AEF＝45°，点P从点E开始沿射线EF方向以 $\sqrt{2}$ cm/秒的速度运动，设运动时间为t秒（0＜t＜6）.过点P作PQ⊥AE，垂足是点Q，连结BQ，CQ若BC＝4cm，DE＝6cm且当t＝2时，四边形ABQC是菱形.

(1)、求AB的长；

(2)、若四边形ABQC的一条对角线等于其中一边，求t的值.

查看试题解析

时间（小时）	1	2	3	4	5
人数	12	17	13	5	3