浙江省杭州市滨江区2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2020-08-21 类型：期末考试

进入出卷网下载

一、选择题

1. 下列交通标志中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若关于x的方程 $x^{2} + a x + a = 0$ 有一个根为-3，则a的值是（）

A、9 B、4.5 C、3 D、-3

查看试题解析
3. 如图，若要使平行四边形ABCD成为菱形，需添加的条件是（）

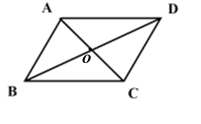A、 $A B = C D$ B、 $∠ A D B = ∠ D B C$ C、 $A O = B O$ D、 $A C ， B D$ 互相垂直

查看试题解析
4. 小明妈妈经营一家服装专卖店，为了合理利用资金，小明帮妈妈对上个月各种型号的服装销售数量进行了一次统计分析，决定在这个月的进货中多进某种型号服装，此时小明应重点参考（）

A、众数 B、平均数 C、加权平均数 D、中位数

查看试题解析
5. 若命题“ $a < 0$ ”不成立，那么a与0的大小关系是（）

A、 $a \geq 0$ B、 $a > 0$ C、 $a \neq 0$ D、 $a = 0$

查看试题解析
6. 用配方法解一元二次方程 $x^{2} - 8 x + 7 = 0$ ，方程可变形为（）

A、 ${(x + 4)}^{2} = 9$ B、 ${(x - 4)}^{2} = 9$ C、 ${(x - 8)}^{2} = 16$ D、 ${(x + 8)}^{2} = 57$

查看试题解析
7. 已知 $(- 2 ， y_{1})$ ， $(- 3 ， y_{2})$ ， $(2 ， y_{3})$ 在反比例函数 $y = - \frac{0.8}{x}$ 图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系为（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{1} > y_{3} > y_{2}$ C、 $y_{3} > y_{2} > y_{1}$ D、 $y_{3} > y_{1} > y_{2}$

查看试题解析
8. 如图，▱ABCD中，AB=4，BC=5，AC的垂直平分线交AD于点E，则△CDE的周长是（）

A、6 B、8 C、9 D、10

查看试题解析
9. 如图，在反比例函数 $y = \frac{k}{x} (x > 0)$ 的图原上有A，B，C，D四点，他们的横坐标依次是1，2，3，4，分别过这些点作x轴和y轴的垂线，图中构成的阴影部分的面积从左到右依次是S₁ ， S₂ ， S₃.则下列结论正确的是（）

A、 $S_{1} = S_{2} + S_{3}$ B、 $S_{1} = 2 S_{2} - S_{3}$ C、 $S_{1} = 2 S_{2} + S_{3}$ D、 $S_{1} = 2 S_{2} + 2 S_{3}$

查看试题解析
10. 在矩形ABCD中，E，P，G，H分别是边AB，BC，CD，DA上的点(不与端点重合)，对于任意矩形ABCD，下面四个结论中正确的是（）
①存在无数个四边形EFGH是平行四边形.②存在无数个四边形EFGH是矩形.③存在且仅有一个四边形EFGH是菱形.④除非矩形ABCD为正方形，否则不存在四边形EFGH是正方形.

A、①② B、①②③ C、①②④ D、①③④

查看试题解析

二、填空题

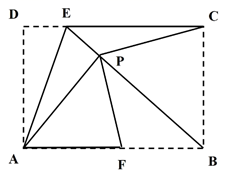
11. 若式子 $\sqrt{2 x - 3}$ 有意义，则x的取值范围是

查看试题解析
12. 已知一个多边形的内角和为540°，则这个多边形是边形．

查看试题解析
13. 一组数据：1，4，4，8，3，10，x，5，5，其平均数5，是则其中位数是.

查看试题解析
14. 超市的一种饮料，平均每天可售出100箱，每箱利润12元，为扩大销售，准备适当降价，据测算，每降价1元，每天可多售出20箱，若要使每天销售这种饮料获利1400元，每箱应降价多少元？设每箱降价x元，则可列方程（不用化简）为： .

查看试题解析
15. 已知 $25 x^{2} + 20 (n - 1) x + 8 n$ 是一个关于x的完全平方式，则常数n=.

查看试题解析
16. 如图，矩形ABCD中，E为CD上一点，F为AB上一点，分别沿AE，CF折叠，D，B两点刚好都落在矩形内一点P，且∠APC=120°，则AB：AD=.

查看试题解析

三、解答题

17. 计算

(1)、 $\sqrt{5} + \sqrt{10} \times \sqrt{50}$

(2)、 $\sqrt{\frac{2}{3}} + \frac{5}{\sqrt{6}}$

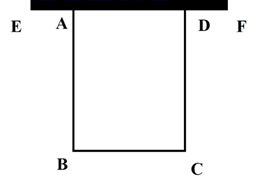
查看试题解析
18. 解一元二次方程：

(1)、 $x^{2} + 2 x = 29$

(2)、 $2 x^{2} - \sqrt{2} x - 1 = 0$

查看试题解析
19. 老李想利用一段5米长的墙(图中EF)，建一个面积为32平方米的矩形养猪圈，另外三面(图中AB，BC，CD)需要自己建筑.老李准备了可以修建20米墙的材料(可以不用完).

(1)、设 $A B = y$ ， $B C = x$ ，求y关于x的函数关系式.

(2)、对于（1）中的函数y的值能否取到8.5？请说明理由.

查看试题解析

20. 某公司计划从两家生产能力相近的制造厂选择一家来承担外销业务，这两家厂生产的皮具款式和材料都符合要求，因此只需要检测皮具质量的克数是否稳定，现从两家提供的样品中各随机抽取了6件进行检查，超过标准质量部分记为正数，不足部分记为负数，若该皮具的标准质量为400克，测得它们质量如下(单位：g)

厂家	超过标准质量的部分
甲	-4	1	0	1	2	0
乙	-2	1	-1	0	1	1

(1)、分别计算甲、乙两厂抽样检测的6件皮具的平均质量各是多少克？

(2)、通过计算，你认为哪一家生产的皮具质量比较稳定？

查看试题解析

21. 如图， $▱$ ABCD中，∠DAB为钝角，AD=1，AB= $\sqrt{2}$ ，且 $▱$ ABCD的面积为1.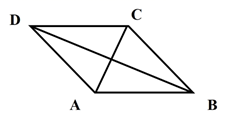

(1)、求 $▱$ ABCD各内角的度数.

(2)、求 $▱$ ABCD的对角线AC，BD的长.

查看试题解析
22. 如图，在矩形ABCO中，点O为坐标原点，点A，C分别在x轴、y轴的正半轴上，OA比OC大2，比AC小2.反比例函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图象经过矩形对角线AC，BO的交点D.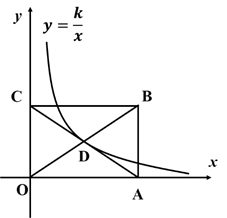

(1)、求OA的长和此反比例函数的表达式

(2)、若反比例函数 $y = \frac{m}{x} (m > 0 ， x > 0)$ 的图象经过矩形ABCO边的中点
①求m的值.

②在双曲线 $y = \frac{k}{x} (k > 0 ， x > 0)$ 上任取一点G，过点G作GE⊥x轴于点E，交双曲线 $y = \frac{k}{x} (k > 0 ， x > 0)$ 于F点，过点G作GK⊥y轴于点K交双曲线 $y = \frac{k}{x} (k > 0 ， x > 0)$ 于H点.求△GHF的面积.

查看试题解析
23. 矩形ABCD中，AB=3，BC=4.点E，F在对角线AC上，点M，N分别在边AD，BC上.

(1)、如图1，若AE=CF=1，M，N分别是AD，BC的中点.求证：四边形EMFN为矩形.

(2)、如图2，若AE=CF=0.5， $A M = C N = x （ 0 < x < 2 ）$ ，且四边形EMFN为矩形，求x的值.

查看试题解析