辽宁省沈阳市大东区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-08-21 类型:期末考试
一、选择题
-
1. 以下是回收、绿色包装、节水、低碳四个标志,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若a>b,则下列式子中一定成立的是( )A、a﹣2<b﹣2 B、3﹣a>3﹣b C、2a>b D、 >3. 下列各式从左到右的变形中,是因式分解的为( )A、x2-1=(x+1)(x-1) B、x2-1+y2=(x+1)(x-1) +y2 C、x(a-b)=ax-bx D、ax+bx+c=x(a+b)+c4. 如图,△DEF是由△ABC经过平移后得到的,且B,E,C,F在同一直线上,则平移的距离是( )
2. 若a>b,则下列式子中一定成立的是( )A、a﹣2<b﹣2 B、3﹣a>3﹣b C、2a>b D、 >3. 下列各式从左到右的变形中,是因式分解的为( )A、x2-1=(x+1)(x-1) B、x2-1+y2=(x+1)(x-1) +y2 C、x(a-b)=ax-bx D、ax+bx+c=x(a+b)+c4. 如图,△DEF是由△ABC经过平移后得到的,且B,E,C,F在同一直线上,则平移的距离是( ) A、线段BE的长度 B、线段EC的长度 C、线段BC的长度 D、线段EF的长度5. 平行四边形一边长12,那么它的两条对角线的长度可能是( )A、8和16 B、10和16 C、8和14 D、8和126. 计算 的结果是( )A、 B、 C、 D、7. 如图, 中,∠B=30°,∠C=90°,将 绕点A按顺时针方向旋转到 的位置,使得点C、A、B1在同一条直线上,那么旋转角等于( )
A、线段BE的长度 B、线段EC的长度 C、线段BC的长度 D、线段EF的长度5. 平行四边形一边长12,那么它的两条对角线的长度可能是( )A、8和16 B、10和16 C、8和14 D、8和126. 计算 的结果是( )A、 B、 C、 D、7. 如图, 中,∠B=30°,∠C=90°,将 绕点A按顺时针方向旋转到 的位置,使得点C、A、B1在同一条直线上,那么旋转角等于( ) A、60° B、90° C、120° D、150°8. 若三角形的各边长分别是8,10和16,则以各边中点为顶点的三角形的周长为( )A、34 B、30 C、29 D、179. 如果9x2+kx+25是一个完全平方式,那么k的值是( )A、15 B、±5 C、30 D、±3010. 如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD的面积的( )
A、60° B、90° C、120° D、150°8. 若三角形的各边长分别是8,10和16,则以各边中点为顶点的三角形的周长为( )A、34 B、30 C、29 D、179. 如果9x2+kx+25是一个完全平方式,那么k的值是( )A、15 B、±5 C、30 D、±3010. 如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD的面积的( )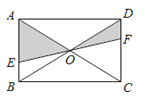 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 因式分解:a2﹣4= .12. 分式 的值为0,则 .13. 已知一个多边形的外角和等于其内角和的 ,则这个多边形的边数为.14. 一次函数y=kx+b(k≠0,k,b为常数)的图象如图所示,则关于x的不等式kx+b<0的解集为.
 15. “端午节”前,商场为促销定价为10元每袋的蜜枣粽子,采取如下方式优惠销售:若一次性购买不超过2袋,则按原价销售;若一次性购买2袋以上,则超过部分按原价的七折付款.张阿姨现有50元钱,那么她最多能买蜜枣粽子袋.16. 等边 中,AB=14.平面内有一点D,BD=6,AD=10, 则CD的长为.
15. “端午节”前,商场为促销定价为10元每袋的蜜枣粽子,采取如下方式优惠销售:若一次性购买不超过2袋,则按原价销售;若一次性购买2袋以上,则超过部分按原价的七折付款.张阿姨现有50元钱,那么她最多能买蜜枣粽子袋.16. 等边 中,AB=14.平面内有一点D,BD=6,AD=10, 则CD的长为.三、解答题
-
17. 分解因式:(1)、3x-12x3;(2)、4m2+2mn+ n2.18. 解分式方程:19. 解不等式组: ,并把该不等式组中的两个不等式的解集在下图所示的数轴上表示出来.
 20. 先化简,再求值: ,其中x=2.21. 如图,正方形ABCD的边长为4,E是边BC上的一点,把 平移到 ,再把 逆时针旋转到 的位置.
20. 先化简,再求值: ,其中x=2.21. 如图,正方形ABCD的边长为4,E是边BC上的一点,把 平移到 ,再把 逆时针旋转到 的位置. (1)、把 平移到 ,则平移的距离为;(2)、四边形AEFD是四边形;(3)、把 逆时针旋转到 的位置,旋转中心是点;(4)、若连接EG,求证: 是等腰直角三角形.22. 某工厂现在平均每天比原计划多生产20台机器,现在生产300台机器所需时间与原计划生产150台机器所需时间相同,求现在平均每天生产多少台机器.23. 我国从 2011年5月1日起在公众场所实行“禁烟”,为配合“禁烟”行动,某校组级开展了“吸烟有害健康”的知识竞赛,共有20道题,答对一道题得10分,答错或不答一道题扣5分.小明参加本次竞赛得分要超过100 分,他至少要答对几道题.24. 已知 中,点O是AC中点,连接BO并延长到D,使OD=OB,连接DA,DC.
(1)、把 平移到 ,则平移的距离为;(2)、四边形AEFD是四边形;(3)、把 逆时针旋转到 的位置,旋转中心是点;(4)、若连接EG,求证: 是等腰直角三角形.22. 某工厂现在平均每天比原计划多生产20台机器,现在生产300台机器所需时间与原计划生产150台机器所需时间相同,求现在平均每天生产多少台机器.23. 我国从 2011年5月1日起在公众场所实行“禁烟”,为配合“禁烟”行动,某校组级开展了“吸烟有害健康”的知识竞赛,共有20道题,答对一道题得10分,答错或不答一道题扣5分.小明参加本次竞赛得分要超过100 分,他至少要答对几道题.24. 已知 中,点O是AC中点,连接BO并延长到D,使OD=OB,连接DA,DC. (1)、如图1,求证:四边形ABCD是平行四边形;(2)、如图2,过点A作AE⊥BC于E,F为AB的中点,连接EF,若∠CAD=45°,且OA=2 ,BE:EC=1:2,求EF的长;(3)、在(2)的条件下,若P是边BC上一动点,当 为等腰三角形时,请直接写出BP的长.25. 如图,一个锐角等于60°的菱形ABCD,将一个60°的∠MAN的顶点与该菱形顶点A重合,以A为旋转中心,按顺时针方向旋转这个60°的∠MAN,使它的两边分别交CB、DC或它们的延长线于点E,F.
(1)、如图1,求证:四边形ABCD是平行四边形;(2)、如图2,过点A作AE⊥BC于E,F为AB的中点,连接EF,若∠CAD=45°,且OA=2 ,BE:EC=1:2,求EF的长;(3)、在(2)的条件下,若P是边BC上一动点,当 为等腰三角形时,请直接写出BP的长.25. 如图,一个锐角等于60°的菱形ABCD,将一个60°的∠MAN的顶点与该菱形顶点A重合,以A为旋转中心,按顺时针方向旋转这个60°的∠MAN,使它的两边分别交CB、DC或它们的延长线于点E,F. (1)、如图1,当BE=DF时,AE与AF的数量关系是;(2)、旋转∠MAN,如图2,当BE≠DF时,(1)的结论是否成立?若成立,加以证明;若不成立,请说明理由;(3)、若菱形ABCD的边长为4,BE=1,请直接写出AF的长.
(1)、如图1,当BE=DF时,AE与AF的数量关系是;(2)、旋转∠MAN,如图2,当BE≠DF时,(1)的结论是否成立?若成立,加以证明;若不成立,请说明理由;(3)、若菱形ABCD的边长为4,BE=1,请直接写出AF的长.