江苏省扬州市江都区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-08-21 类型:期末考试
一、选择题
-
1. 下列数学符号中,既是轴对称图形又是中心对称图形的是( )A、
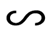 B、
B、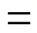 C、
C、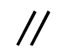 D、
D、 2. 下列调查中适合采用普查的是( )A、调查某一居民小区感染新冠病毒的人数 B、调查鞋厂生产的鞋底能承受的弯折次数 C、调查市场上某种饮料中防腐剂的含量 D、了解扬州市居民收看扬州电视台《今日生活》栏目的情况3. 下列说法中不正确的是( )A、抛掷一枚质量均匀的硬币,硬币落地时正面朝上是随机事件 B、把4个球放入三个抽屉中,其中一个抽屉至少有两个球是必然事件 C、为了呈现某个月的气温变化情况,应选择的统计图为扇形统计图 D、从一副扑克牌中任意抽取1张,摸到的牌是“A”的可能性比摸到的牌是“红桃”可能性小4. 在同一平面直角坐标系中,函数y=﹣x+k与y= (k为常数,且k≠0)的图象大致是( )A、
2. 下列调查中适合采用普查的是( )A、调查某一居民小区感染新冠病毒的人数 B、调查鞋厂生产的鞋底能承受的弯折次数 C、调查市场上某种饮料中防腐剂的含量 D、了解扬州市居民收看扬州电视台《今日生活》栏目的情况3. 下列说法中不正确的是( )A、抛掷一枚质量均匀的硬币,硬币落地时正面朝上是随机事件 B、把4个球放入三个抽屉中,其中一个抽屉至少有两个球是必然事件 C、为了呈现某个月的气温变化情况,应选择的统计图为扇形统计图 D、从一副扑克牌中任意抽取1张,摸到的牌是“A”的可能性比摸到的牌是“红桃”可能性小4. 在同一平面直角坐标系中,函数y=﹣x+k与y= (k为常数,且k≠0)的图象大致是( )A、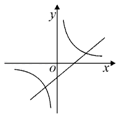 B、
B、 C、
C、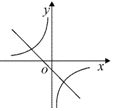 D、
D、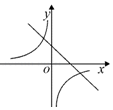 5. 化简: 的结果是( )A、 B、 C、﹣ D、﹣6. 下列说法中错误的是( )A、有一组邻边相等的矩形是正方形 B、在反比例函数 中,y随x的增大而减小 C、顺次连接矩形各边中点得到的四边形是菱形 D、如果用反证法证明“三角形中至少有一个内角小于或等于60°”,首先应假设这个三角形中每一个内角都大于60°7. 已知点 在反比例函数 (m为常数)的图像上,则下列关系式正确的是( )A、y3<y2<y1 B、y2<y3<y1 C、y3<y1<y2 D、y2<y1<y38. 如图,在 ABCD中,∠ABC=45°,BC=4,点F是CD上一个动点,以FA、FB为邻边作另一个 AEBF,当F点由D点向C点运动时,下列说法正确的选项是( )
5. 化简: 的结果是( )A、 B、 C、﹣ D、﹣6. 下列说法中错误的是( )A、有一组邻边相等的矩形是正方形 B、在反比例函数 中,y随x的增大而减小 C、顺次连接矩形各边中点得到的四边形是菱形 D、如果用反证法证明“三角形中至少有一个内角小于或等于60°”,首先应假设这个三角形中每一个内角都大于60°7. 已知点 在反比例函数 (m为常数)的图像上,则下列关系式正确的是( )A、y3<y2<y1 B、y2<y3<y1 C、y3<y1<y2 D、y2<y1<y38. 如图,在 ABCD中,∠ABC=45°,BC=4,点F是CD上一个动点,以FA、FB为邻边作另一个 AEBF,当F点由D点向C点运动时,下列说法正确的选项是( )① AEBF的面积先由小变大,再由大变小;② AEBF的面积始终不变;③线段EF最小值为
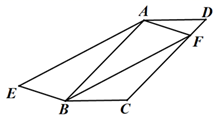 A、① B、② C、①③ D、②③
A、① B、② C、①③ D、②③二、填空题
-
9. 比较大小: (填“>”或“<”=).10. 如图,小正方形方格的边长都是1,点A、B、C、D、O都是小正方形的顶点.若 COD是由 AOB绕点O按顺时针方向旋转一次得到的,则至少需要旋转°.
 11. 在一个不透明的盒子里装有黑、白两种颜色的球共50只,这些球除颜色外其余完全相同.小颖做摸球实验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中.不断重复上述过程,下表是实验中的一组统计数据:
11. 在一个不透明的盒子里装有黑、白两种颜色的球共50只,这些球除颜色外其余完全相同.小颖做摸球实验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中.不断重复上述过程,下表是实验中的一组统计数据:摸球的次数n
100
200
300
500
800
1 000
3 000
摸到白球的次数m
65
124
178
302
481
620
1845
摸到白球的频率
0.65
0.62
0.593
0.604
0.601
0.620
0.615
请估计:当n很大时,摸到白球的频率将会接近;(精确到0.1)
12. 与最简二次根式 是同类二次根式,则a=.13. 若式子 在实数范围内有意义,则 的取值范围是.14. 若关于x的分式方程 有增根,则m=.15. 已知1<x≤2,化简 的结果为.16. 如图,等边三角形ABO的顶点A在反比例函数y= (x<0)的图象上,边BO在x轴上,等边三角形ABO的面积为 ,则k=.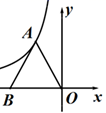 17. 如图, ABC中,AB=AC=4,以AC为斜边作Rt ADC,使∠ADC=90°,∠CAD=∠CAB=30°,E、F分别是BC、AC的中点,则ED=.
17. 如图, ABC中,AB=AC=4,以AC为斜边作Rt ADC,使∠ADC=90°,∠CAD=∠CAB=30°,E、F分别是BC、AC的中点,则ED=.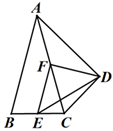 18. 如图,以Rt ABC的斜边AB为一边,在AB的右侧作正方形ABED,正方形对角线交于点O,连接CO,如果AC=4,CO= ,那么BC=.
18. 如图,以Rt ABC的斜边AB为一边,在AB的右侧作正方形ABED,正方形对角线交于点O,连接CO,如果AC=4,CO= ,那么BC=.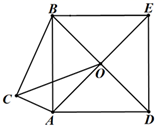
三、解答题
-
19. 计算:(1)、(2)、20. 解方程:(1)、(2)、21. 先化简,再求值: ,其中 .22. 为了解家长们对“扬州智慧学堂”平台的知晓程度(“A.非常了解”“B.了解”“C.基本了解”“D.不太了解”),教育局随机调查了若干家长.根据调查结果绘制成如下两幅不完整的统计图:
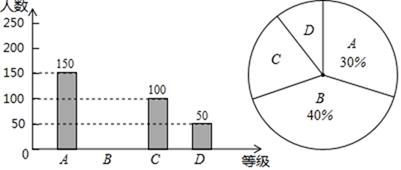 (1)、本次随机调查的样本容量是 , 扇形统计图中表示“A”的扇形圆心角为°;(2)、补全条形统计图;(3)、估计在30000名家长中不太了解“扬州智慧学堂”平台的人数.23. 为了应对新型冠状病毒肺炎疫情,某工厂接到600件防护服的紧急生产任务,为了尽快完成任务,该工厂实际每天生产防护服的件数比原来每天多50%,结果提前10天完成任务,那么原来每天生产防护服多少件?24. 如图,在菱形ABCD中,对角线AC,BD相交于点O,DE∥AC,AE∥BD.
(1)、本次随机调查的样本容量是 , 扇形统计图中表示“A”的扇形圆心角为°;(2)、补全条形统计图;(3)、估计在30000名家长中不太了解“扬州智慧学堂”平台的人数.23. 为了应对新型冠状病毒肺炎疫情,某工厂接到600件防护服的紧急生产任务,为了尽快完成任务,该工厂实际每天生产防护服的件数比原来每天多50%,结果提前10天完成任务,那么原来每天生产防护服多少件?24. 如图,在菱形ABCD中,对角线AC,BD相交于点O,DE∥AC,AE∥BD. (1)、求证:四边形AODE是矩形;(2)、若菱形边长为10,面积为96,求矩形AODE周长.25. 如图1、2,点E为正方形ABCD边DC的中点,依据正方形的对称性,请仅用一把无刻度的直尺(仅用于过任意两点作直线、连接任意两点、延长任意线段)按要求画图.(不写画法,保留作图痕迹).
(1)、求证:四边形AODE是矩形;(2)、若菱形边长为10,面积为96,求矩形AODE周长.25. 如图1、2,点E为正方形ABCD边DC的中点,依据正方形的对称性,请仅用一把无刻度的直尺(仅用于过任意两点作直线、连接任意两点、延长任意线段)按要求画图.(不写画法,保留作图痕迹).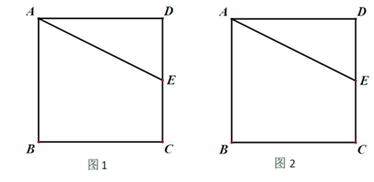 (1)、在图1中,画出∠B的平分线和AD边的中点F;(2)、在图2中,画出EF⊥AB,垂足为点F.26. 如图,反比例函数 (k>0)的图象与正比例函数 的图象交于A、B两点(点A在第一象限).
(1)、在图1中,画出∠B的平分线和AD边的中点F;(2)、在图2中,画出EF⊥AB,垂足为点F.26. 如图,反比例函数 (k>0)的图象与正比例函数 的图象交于A、B两点(点A在第一象限).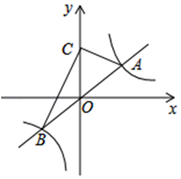 (1)、当点A的横坐标为2时.求k的值;(2)、若k=12,点C为y轴正半轴上一点,∠ACB=90°
(1)、当点A的横坐标为2时.求k的值;(2)、若k=12,点C为y轴正半轴上一点,∠ACB=90°①求 ACB的面积;
②以A、B、C、D为顶点作平行四边形,直接写出第四个顶点D的坐标.
27. 在函数的学习中,我们经历了“确定函数表达式——画函数图象——利用函数图象研究函数性质——利用图像解决问题”的学习过程.我们可以借鉴这种方法探究函数 的图像性质. (1)、补充表格,并画出函数的图象
(1)、补充表格,并画出函数的图象①列表:
x
…
-3
-1
0
2
3
5
…
y
…
-1
-2
-4
4
1
…
②描点并连线,画图.
(2)、观察图像,写出该函数图象的一个增减性特征:;(3)、函数 的图像是由函数 的图像如何平移得到的? , 其对称中心的坐标为;(4)、根据上述经验,猜一猜函数 的图像大致位置,结合图像直接写出y≥3时,x的取值范围.28. 如图1,矩形ABCD中,AB=3,BC=4 ,将矩形ABCD绕着点A顺时针旋转,得到矩形BEFG. (1)、当点E落在BD上时,则线段DE的长度等于 ;(2)、如图2,当点E落在AC上时,求 BCE的面积;(3)、如图3,连接AE、CE、AG、CG,判断线段AE与CG的位置关系且说明理由,并求CE 2+AG 2的值;(4)、在旋转过程中,请直接写出 的最大值.
(1)、当点E落在BD上时,则线段DE的长度等于 ;(2)、如图2,当点E落在AC上时,求 BCE的面积;(3)、如图3,连接AE、CE、AG、CG,判断线段AE与CG的位置关系且说明理由,并求CE 2+AG 2的值;(4)、在旋转过程中,请直接写出 的最大值.