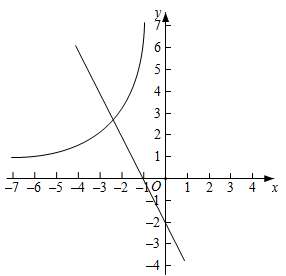江苏省溧阳市2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-08-21 类型:期末考试
一、选择题
-
1. 下列手机APP图标中,不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各式 , , , , 中分式有( )A、2个 B、3个 C、4个 D、5个3. 下列式子中,为最简二次根式的是( )A、 B、 C、 D、4. 已知实数a<0,则下列事件中是必然事件的是( )A、3a>0 B、a-3<0 C、a+3>0 D、a3>05. 为了了解我市今年6000名学生参加初中毕业考试数学成绩情况,从中抽取了500名考生的成绩进行统计,下列说法:①这6000名学生的成绩的全体是总体;②每个考生是个体;③500名考生是总体的一个样本;④样本容量是500.其中说法正确的有( )A、4个 B、3个 C、2个 D、1个6. 如图,平行四边形ABCD的对角线交于点O,且AB=8,△OCD的周长为20,则平行四边形ABCD的两条对角线的和是( )
2. 下列各式 , , , , 中分式有( )A、2个 B、3个 C、4个 D、5个3. 下列式子中,为最简二次根式的是( )A、 B、 C、 D、4. 已知实数a<0,则下列事件中是必然事件的是( )A、3a>0 B、a-3<0 C、a+3>0 D、a3>05. 为了了解我市今年6000名学生参加初中毕业考试数学成绩情况,从中抽取了500名考生的成绩进行统计,下列说法:①这6000名学生的成绩的全体是总体;②每个考生是个体;③500名考生是总体的一个样本;④样本容量是500.其中说法正确的有( )A、4个 B、3个 C、2个 D、1个6. 如图,平行四边形ABCD的对角线交于点O,且AB=8,△OCD的周长为20,则平行四边形ABCD的两条对角线的和是( ) A、40 B、28 C、24 D、127. 若点(x1 , y1),(x2 , y2),(x3 , y3)都是反比例函数y=﹣图象上的点,并且y1<0<y2<y3 , 则下列各式中正确的是( )A、x1<x2<x3 B、x1<x3<x2 C、x2<x1<x3 D、x2<x3<x18. 关于x的方程 的解是正数,则a的取值范围是( )A、a>-1 B、a>-1且a≠0 C、a<-1 D、a<-1且a≠-2
A、40 B、28 C、24 D、127. 若点(x1 , y1),(x2 , y2),(x3 , y3)都是反比例函数y=﹣图象上的点,并且y1<0<y2<y3 , 则下列各式中正确的是( )A、x1<x2<x3 B、x1<x3<x2 C、x2<x1<x3 D、x2<x3<x18. 关于x的方程 的解是正数,则a的取值范围是( )A、a>-1 B、a>-1且a≠0 C、a<-1 D、a<-1且a≠-2二、填空题
-
9. 当 时,二次根式 有意义10. 若分式 的值为0,则 =.11. “在数轴上任取一个点,这个点所表示的数是有理数”这一事件是(填“必然事件”、“不可能事件”或“随机事件”).12. 一个样本的50个数据分别落在5个小组内,第1、2、3、4组的数据的个数分别为2、8、15、5,则第5组的频率为 。13. 平行四边形ABCD中,∠A+∠C=120°,则∠B=度.14. 在矩形ABCD中,对角线AC、BD交于点O,若 ,则 .15. 若顺次连接四边形ABCD四边中点形成的四边形为矩形,则四边形ABCD满足的条件为.16. 如图,已知正方形ABCD的边长为2,对角线AC、BD相交于点O,AE平分∠BAC交BD于点E,则BE的长为.
 17. 如图,点A在函数y= (x>0)的图象上,点B在函数y= (x>0)的图象上,点C在x轴上.若AB∥x轴,则△ABC的面积为 .
17. 如图,点A在函数y= (x>0)的图象上,点B在函数y= (x>0)的图象上,点C在x轴上.若AB∥x轴,则△ABC的面积为 .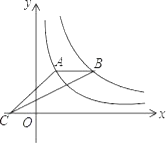 18. 如图,在Rt△ABC中,∠ABC=90°,AC=5,BC=4,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是.
18. 如图,在Rt△ABC中,∠ABC=90°,AC=5,BC=4,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是.
三、 解答题
-
19. 化简或计算:(1)、 ;(2)、 ;(3)、 ;(4)、20. 解下列分式方程:(1)、 ;(2)、21. 方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(-3,-1).

( 1 )试作出△ABC以C为旋转中心,沿逆时针方向旋转90°后的图形△A1B1C;
( 2 )以原点O为对称中心,再画出与△ABC关于原点O对称的△A2B2C2 , 并写出点C2的坐标.
22. 某校开展八年级“新冠疫情防控”学生知识竞赛,现抽取部分学生的竞赛成绩(满分为100分,得分均为整数)进行统计,绘制了图中两幅不完整的统计图.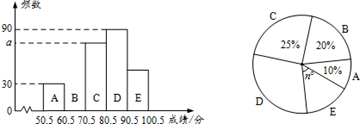
根据图中信息,回答下列问题:
(1)、a= , n=;(2)、补全频数分布直方图;(3)、该校八年级共有1200名学生.若成绩在80分以上的为优秀,请你估计该校成绩优秀的学生人数.23. 如图,在△ABC中,∠ACB=90°,D是BC边上的一点,分别过点A、B作BD、AD的平行线交于点E,且 AB平分∠EAD. (1)、求证:四边形EADB是菱形;(2)、连接EC,当∠BAC=60°,BC= 时,求△ECB的面积.24. 小敏去超市购买某商品,第一次按原价购买,用了60元,几天后,正好遇上这种商品八折出售,他用80元又买了一些,两次一共购买了40公斤,请问这种商品的原价是多少元?
(1)、求证:四边形EADB是菱形;(2)、连接EC,当∠BAC=60°,BC= 时,求△ECB的面积.24. 小敏去超市购买某商品,第一次按原价购买,用了60元,几天后,正好遇上这种商品八折出售,他用80元又买了一些,两次一共购买了40公斤,请问这种商品的原价是多少元?