江苏省泰州医药高新区2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2020-08-21 类型：期末考试

进入出卷网下载

一、选择题

1. 下列防控疫情的图标中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列调查中，最适合采用抽样调查的是（）

A、对某地区现有的16名百岁以上老人睡眠时间的调查 B、对“神舟十一号”运载火箭发射前零部件质量情况的调查 C、对某校九年级三班学生视力情况的调查 D、对某市场上某一品牌电脑使用寿命的调查

查看试题解析
3. 如果把 $\frac{5 x}{x + y}$ 的x与y都扩大10倍，那么这个代数式的值（）

A、扩大10倍 B、扩大50倍 C、不变 D、缩小到原来的 $\frac{1}{10}$

查看试题解析
4. 一元二次方程 $x^{2} ﹣ 4 x + 4 = 0$ 的根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法判断

查看试题解析
5. 设a＞0，b＞0，则下列运算错误的是（）

A、 $\sqrt{a b}$ ＝ $\sqrt{a}$ · $\sqrt{b}$ B、( $\sqrt{a}$ )²＝a C、 $\sqrt{a + b}$ ＝ $\sqrt{a}$ ＋ $\sqrt{b}$ D、 $\sqrt{\frac{a}{b}}$ ＝ $\frac{\sqrt{a}}{\sqrt{b}}$

查看试题解析
6. 若点M(－2，y₁)，N(－1，y₂)，P(3，y₃)在双曲线 $y = - \frac{6}{x}$ 上，则y₁ ， y₂ ， y₃由小到大的顺序为（）

A、y₁＜y₂＜y₃ B、y₂＜y₃＜y₁ C、y₃＜y₁＜y₂ D、y₃＜y₂＜y₁

查看试题解析

二、填空题

7. 若分式 $\frac{x + 1}{x - 1}$ 的值为0，则x的值是．

查看试题解析
8. 一个不透明的袋子中，袋中有1 个红球，2 个白球和3 个黑球，这些球除颜色外均相同，将球摇匀后，从袋子中任意摸出一个球，摸到（填“红”或“白”或“黑”）球的可能性最大.

查看试题解析
9. 已知反比例函数 $y = \frac{k}{x}$ 的图象经过点A（-2，3），则 $k$ =；

查看试题解析
10. 如图， $D E$ 是 $△ A B C$ 的中位线， $D E = 2$ cm， $A B + A C = 12$ cm，则梯形 $D B C E$ 的周长为cm.

查看试题解析
11. 已知方程 $x^{2} - 5 x + 2 = 0$ 的两个解分别为 $x_{1}$ 、 $x_{2}$ ，则 $x_{1} + x_{2} - x_{1} \cdot x_{2}$ 的值为.

查看试题解析
12. 菱形两条对角线长分别为 $\sqrt{2}$ 、 $\sqrt{6}$ ，则这个菱形的面积为.

查看试题解析
13. 化简 $\sqrt{1 - x} + \sqrt{x - 1}$ ＝.

查看试题解析
14. 若关于x的方程 $\frac{2}{x - 2} + \frac{x + m}{2 - x} = 2$ 有增根，则m的值是

查看试题解析
15. 如图，在▱ABCD中，AB=2，BC=3，∠ABC=60°，对角线AC与BD交于点O，将直线l绕点O按顺时针方向旋转，分别交AD、BC于点E、F，则四边形ABFE周长的最小值是.

查看试题解析
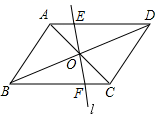16. 如图正方形ABCD边长为2，E为CD边中点，P为射线BE上一点（P不与B重合），若△PDC为直角三角形，则BP＝.

查看试题解析

三、解答题

17. 计算.

(1)、 $\sqrt{8} - \sqrt{2} - \sqrt{\frac{1}{2}}$

(2)、 $2 \sqrt{18} \times 6 \sqrt{3} \div 3 \sqrt{2}$

查看试题解析
18. 先化简，再求值： $\frac{2}{a - 2} + \frac{a^{2} - 6 a + 9}{a^{2} - 4} \div \frac{a - 3}{a + 2}$ ，其中 $a = \sqrt{3} + 2$ .

查看试题解析
19. 解方程

(1)、 $\frac{x - 3}{x - 2} = \frac{1}{2 - x}$

(2)、 $x^{2} - 4 x - 5 = 0$

查看试题解析
20. 已知x、y为实数，且 $\sqrt{4 - x} + y^{2}$ ﹣6y+9＝0，

(1)、分别求出x、y的值；

(2)、求 $\frac{1}{\sqrt{2 x}} + \frac{\sqrt{6}}{\sqrt{y}}$ 的值．

查看试题解析
21. 列方程解应用题：
中华优秀传统文化是中华民族的“根”和“魂”.为传承优秀传统文化，某校购进《西游记》和《三国演义》若干套，其中每套《西游记》的价格比每套《三国演义》的价格多40元，用3200元购买《三国演义》的套数是用2400元购买《西游记》套数的2倍，求每套《三国演义》的价格.

查看试题解析
22. 某公司共有400名销售人员，为了解该公司销售人员某季度商品销售情况，随机抽取部分销售人员该季度的销售数量，并把所得数据整理后绘制成如下统计图表进行分析.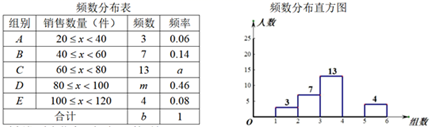

请根据上述统计图表，解答下列问题：

(1)、表中a＝， b＝；

(2)、补全频数分布直方图；

(3)、如果该季度销量不低于80件的销售人员将被评为“优秀员工”，试估计该季度被评为“优秀员工”的人数.

查看试题解析
23. 某校绿色行动小组组织一批人参加植树活动，完成任务的时间y（h）是参加植树人数 $x$ （人）的反比例函数，且当 $x = 20$ 人时， $y = 3 h$ .

(1)、若平均每人每小时植树4棵，则这次共计要植树棵；

(2)、当 $x = 80$ 时，求y的值；

(3)、为了能在 $1.5 h$ 内完成任务，至少需要多少人参加植树？

查看试题解析
24. 已知关于x的一元二次方程x²−2x–m²＋1＝0.

(1)、求证：该方程有两个实数根；

(2)、若该方程的两个实数根都为正数，求m的取值范围；

(3)、若该方程的两个实数根x₁、x₂满足x₁－x₂＝2，求m的值.

查看试题解析
25. 已知在Rt△ABC中，∠ACB=90°，现按如下步骤作图：
①分别以A，C为圆心，a为半径（a＞ $\frac{1}{2}$ AC）作弧，两弧分别交于M，N两点；
②过M，N两点作直线MN交AB于点D，交AC于点E；
③将△ADE绕点E顺时针旋转180°，设点D的像为点F．

(1)、请在图中直线标出点F并连接CF；

(2)、求证：四边形BCFD是平行四边形；

(3)、当∠B为多少度时，四边形BCFD是菱形．

查看试题解析
26. 如图在平面直角坐标系中，O为原点，A、B两点分别在y轴、x轴的正半轴上，△AOB的一条内角平分线、一条外角平分线交于点P，P在反比例函数 $y = \frac{4}{x}$ 的图像上.

(1)、求点P的坐标；

(2)、若OA＝OB，则①∠P的度数为 ▲ ；②求出此时直线AB的函数关系式；

(3)、如果直线AB的关系式为y＝kx＋n，且0＜n＜2，作反比例函数 $y = - \frac{n}{x}$ ，过点P(0，1)作x轴的平行线与 $y = \frac{4}{x}$ 的图像交于点M，与 $y = - \frac{n}{x}$ 的图像交于点N，过点N作y轴的平行线与y＝kx＋n的图像交于点Q，若MN＋QN的和始终是一个定值d，求此时k的值及定值d.

查看试题解析