吉林省松原市长岭县2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-08-19 类型:期末考试
一、选择题:本大题共6个小题,每小题2分,共12分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 要使二次根式 有意义,则 必需满足( )A、 B、 C、 为任何实数 D、 为非负数2. 下列二次根式中是最简二次根式的是( )A、 B、 C、 D、3. 下列函数中, 是 的正比例函数的是( )A、 B、 C、 D、4. 如图,对四边形 ABCD 增加条件,使之成为平行四边形,下面添加不正确的是( )
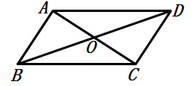 A、 B、 C、 D、 与 相互平分5. 已知, 是一次函数 的图象上三个点,则 、 、 的大小关系是( )A、 B、 C、 D、6. 如图,平行四边形 的对角线 与 交于点 , , , ,则 的长为( )
A、 B、 C、 D、 与 相互平分5. 已知, 是一次函数 的图象上三个点,则 、 、 的大小关系是( )A、 B、 C、 D、6. 如图,平行四边形 的对角线 与 交于点 , , , ,则 的长为( )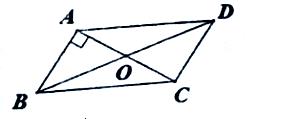 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,满分24分,将答案填在答题纸上)
-
7. 计算: 的结果是.8. 点 在一次函数 的图象上,那么 .9. 有两根木棒,分别长 、 ,要再在 的木棒上取一段,用这三根木棒为边做成直角三角形,则第三根木棒要取的长度是 .10. 在数轴上表示实数 的点如图所示,化简 的结果为 .
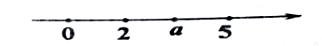 11. 如图,在平面直角坐标系中, , ,以点 为圆心, 长为半径画弧,交 轴的负半轴于点 ,则点 的坐标为 .
11. 如图,在平面直角坐标系中, , ,以点 为圆心, 长为半径画弧,交 轴的负半轴于点 ,则点 的坐标为 .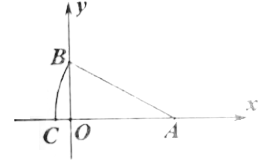 12. 三个正方形如图摆放,其中两个正方形的面积为 , ,则第三个正方形面积为 .
12. 三个正方形如图摆放,其中两个正方形的面积为 , ,则第三个正方形面积为 . 13. 李老师开车从甲地到相距 千米的乙地,如果油箱剩余油量 (升)与行驶里程 (千米)之间是一次函数关系,其图像如图所示,那么到达乙地时油箱剩余油量是升.
13. 李老师开车从甲地到相距 千米的乙地,如果油箱剩余油量 (升)与行驶里程 (千米)之间是一次函数关系,其图像如图所示,那么到达乙地时油箱剩余油量是升.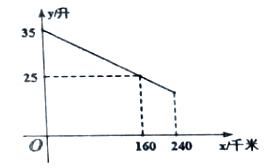 14. 小明利用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示的菱形,并测得 ,接着活动学具成为图2所示的正方形,并测得 ,则图1中对角线 长为 .
14. 小明利用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示的菱形,并测得 ,接着活动学具成为图2所示的正方形,并测得 ,则图1中对角线 长为 .
三、解答题:共84分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
-
15. 计算: .16. 计算: .17. 已知 , ,求代数式 的值.18. 已知 与 成正比例,当 时, .(1)、求 与 之间的函数关系式.(2)、判断点 是否是函数图象上的点,并说明理由.19. 一次函数 的图象与正比例函数 ( 是常数,且 )的图象都经过点 .
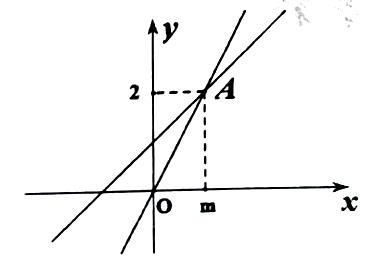 (1)、求正比例函数的表达式;(2)、利用函数图象直接写出当 时, 的取值范围.20. 在边长为 的正方形网格中, 的三个顶点均在格点上,请按要求完成下列各题:
(1)、求正比例函数的表达式;(2)、利用函数图象直接写出当 时, 的取值范围.20. 在边长为 的正方形网格中, 的三个顶点均在格点上,请按要求完成下列各题: (1)、线段BC的长为 , 的面积为;(2)、画出 (点 在格点上),使 (画出所有可能情形);(3)、试说明:21. 如图是甲、乙两人从同一地点出发后路程随时间变化的图像.根据图象回答下列问题:
(1)、线段BC的长为 , 的面积为;(2)、画出 (点 在格点上),使 (画出所有可能情形);(3)、试说明:21. 如图是甲、乙两人从同一地点出发后路程随时间变化的图像.根据图象回答下列问题: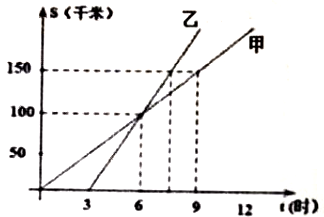 (1)、在此变化过程中,自变量是:;(2)、甲的速度乙的速度(填“大于”“等于”或“小于”)(3)、甲出发后几小时与乙相遇:;(4)、甲比乙先走多长时间:;(5)、 时,甲在乙的(填“前面”“后面”或“相同位置”)(6)、若行驶的路程为 千米,则甲行驶了小时,乙行驶了小时22. 观察下列各式:
(1)、在此变化过程中,自变量是:;(2)、甲的速度乙的速度(填“大于”“等于”或“小于”)(3)、甲出发后几小时与乙相遇:;(4)、甲比乙先走多长时间:;(5)、 时,甲在乙的(填“前面”“后面”或“相同位置”)(6)、若行驶的路程为 千米,则甲行驶了小时,乙行驶了小时22. 观察下列各式:① ;② ;③ ;...
(1)、请观察规律,并写出第④个等式:;(2)、请用含 的式子写出你猜想的规律:;(3)、证明(2)中的结论.23. 某玉米种子的价格为 元 ,如果一次性购买 以上的种子,超过 部分的种子的价格打 折.(1)、根据题意,补充下表:购买种子的重量
付款金额/元
(2)、设购买种子的重量为 ,付款金额为 元,求 与 的函数关系式;(3)、若王伯伯一次性购买该种子花了 元,求他购买种子的重量.24. 如图,在 中, 是 边上的一点, 是 的中点,过 点作 的平行线交 的延长线于点 ,且 ,连接 . (1)、证明: ;(2)、当 满足什么条件时,四边形 是矩形?并说明理由.25. 提出问题:如图①,在正方形 中,点 分别在边 上,若 于点 ,则 .类比探究:
(1)、证明: ;(2)、当 满足什么条件时,四边形 是矩形?并说明理由.25. 提出问题:如图①,在正方形 中,点 分别在边 上,若 于点 ,则 .类比探究: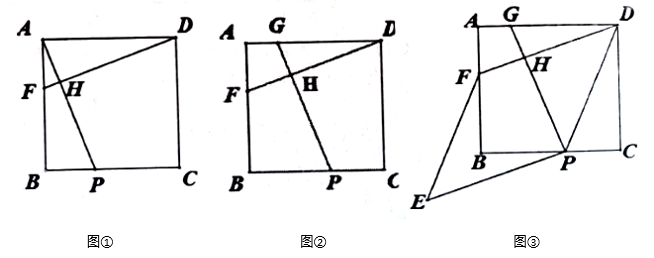 (1)、如图②,在正方形 中,点 分别在边 上,若 于点 ,探究线段 与 的数量关系,并说明理由.(2)、如图③,在正方形 中,点 分别在边 上, 于点 ,将线段 绕点 逆时针旋转 得到线段 ,连接 ,若四边形 为菱形,探究 和 的数量关系,并说明理由.26. 如图,直线 与 轴交于点 ,与直线 相交于点 .
(1)、如图②,在正方形 中,点 分别在边 上,若 于点 ,探究线段 与 的数量关系,并说明理由.(2)、如图③,在正方形 中,点 分别在边 上, 于点 ,将线段 绕点 逆时针旋转 得到线段 ,连接 ,若四边形 为菱形,探究 和 的数量关系,并说明理由.26. 如图,直线 与 轴交于点 ,与直线 相交于点 . (1)、求点 的坐标;(2)、动点 从原点 出发,以每秒 个单位长度的速度在线段 上向点 作匀速运动,连接 ,设运动时间为 秒, 的面积为 ,求 关于 的函数关系式(3)、若点 是 轴上的点,点 是坐标平面内的点若以 为顶点的四边形是菱形,请直接写出点 的坐标.
(1)、求点 的坐标;(2)、动点 从原点 出发,以每秒 个单位长度的速度在线段 上向点 作匀速运动,连接 ,设运动时间为 秒, 的面积为 ,求 关于 的函数关系式(3)、若点 是 轴上的点,点 是坐标平面内的点若以 为顶点的四边形是菱形,请直接写出点 的坐标.