广东省阳江市阳东区2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2020-08-19 类型：期末考试

进入出卷网下载

一、选择题：本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 二次根式 $\sqrt{x - 2}$ 有意义的条件是（）

A、 $x > 2$ B、 $x < 2$ C、 $x \geq 2$ D、 $x \leq 2$

查看试题解析
2. 下列各组数中能够作为直角三角形的三边长的是（　　）

A、1，2，3 B、2，3，4 C、3，4，5 D、4，5，6

查看试题解析
3. 一组数据2,3,4,6,6,7的众数是（）

A、3 B、4 C、5 D、6

查看试题解析
4. 若函数 $y = k x + b$ 是正比例函数，且 $y$ 随 $x$ 的增大而减小，则下列判断正确的是（）

A、 $k > 0$ B、 $k < 0$ C、 $b > 0$ D、 $b < 0$

查看试题解析
5. 如图，将 $▱ A B C D$ 的一边BC延长至点E，若 $∠ A = 110^{\circ}$ ，则 $∠ 1$ 等于（）

A、 $110^{\circ}$ B、 $35^{\circ}$ C、 $70^{\circ}$ D、 $55^{\circ}$

查看试题解析
6. 若 $b > 0$ ，则一次函数 $y = - x + b$ 的图像大致是（）

A、 B、 C、 D、

查看试题解析
7. 某校九年级体育模拟测试中，六名男生引体向上的成绩如下（单位：个）：10,6,9,11,8,10，下列关于这组数据描述正确的是（）

A、中位数是10 B、众数是10 C、平均数是9.5 D、方差是6

查看试题解析
8. 已知 $y$ 是 $x$ 的一次函数，下表列出了部分 $y$ 与 $x$ 的对应值：

$x$

-1

0

1

2

$y$

-2

-1

0

$a$

则 $a$ 的值为（）

A、-2 B、1 C、2 D、3

查看试题解析
9. 如图，在平面直角坐标系中，菱形ABCD的边长为6，它的一边AB在 $x$ 轴上，且AB的中点是坐标原点，点D在 $y$ 轴正半轴上，则点C的坐标为（）

A、 $(3 \sqrt{3} ， 3)$ B、 $(3 ， 3 \sqrt{3})$ C、 $(6 ， 3)$ D、 $(6 ， 3 \sqrt{3})$

查看试题解析
10. 点 $P (x ， y)$ 在第一象限内，且 $x + y = 6$ ，点 $A$ 的坐标为 $(4 ， 0)$ ，设 $Δ O P A$ 的面积为 $S$ ，则下列图像中，能正确反映面积 $S$ 与 $x$ 之间的函数关系式的图像是（）

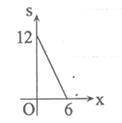A、 B、 C、 D、

查看试题解析

二、填空题（本大题共7个小题,每小题4分,共28分）

11. 计算： $\sqrt{18} - \sqrt{2}$ = ．

查看试题解析
12. 下表是某校女子羽毛球对队员的年龄分布：

年龄/岁

13

14

15

16

人数

1

1

2

1

则该校女子排球队队员年龄的中位数为岁.

查看试题解析
13. 函数 $y = k x$ 与 $y = 6 - x$ 的图像如图所示，则 $k =$ ．

查看试题解析
14. 如图，平行四边形ABCD的对角线AC，BD相交于点 $O$ ，请你添加一个适当的条件使其称为菱形．（只填一个即可）

查看试题解析
15. 某中学为了选拔一名运动员参加区运动会 $100 m$ 短跑比赛，有甲、乙、丙3名运动员备选，他们 $100 m$ 短跑的平均成绩和方差如下表所示：

甲

乙

丙

$\bar{x}$

12.83秒

12.85秒

12.83

$s^{2}$

2.1

1.1

1.1

如果要选择一名成绩优秀且稳定的人去参赛，应派去.

查看试题解析
16. 如图，一木杆在离地面 $1.5 m$ 处折断，木杆顶端落在离木杆底端 $2 m$ 处，则木杆折断之前的高为 $(m)$ ．

查看试题解析
17. 已知 $a, b, c$ 是 $Δ A B C$ 的三边长，且满足关系式 $\sqrt{a - 1} + | b - \sqrt{2} | + {(c - \sqrt{3})}^{2} = 0$ ，则 $Δ A B C$ 的形状为.

查看试题解析

三、解答题（一）：本大题共3个小题,每小题6分,共18分.

18. 计算： $\sqrt{27} + \sqrt{4} - {(π - \sqrt{2})}^{0} - \sqrt{12}$

查看试题解析
19. 如图，平行四边形ABCD的对角线AC、BD相交于点O，EF过点O与AD、BC分别相交于点E、F，求证：OE=OF．

查看试题解析
20. 某篮球队对队员进行定点投篮测试，每人每天投篮10次，现对甲队员在五天中进行球数（单位：个）进行统计，结果如表：

甲

7

9

7

8

9

求甲进球的平均数和方差.

查看试题解析

四、解答题（二）（本大题共3小题，每小题8分，共24分）

21. 如图，正方形网格的每个小方格都是边长为1的正方形， $Δ A B C$ 的顶点都在格点上.

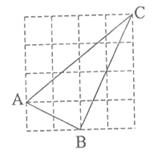(1)、分别求出 $A B ， B C ， A C$ 的长；

(2)、试判断 $Δ A B C$ 是什么三角形，并说明理由.

查看试题解析
22. 如图，BD是 $Δ A B C$ 的角平分线，过点D作 $D E / / B C$ 交 $A B$ 于点E， $D F / / A B$ 交BC于点F.

(1)、求证：四边形BEDF为菱形；

(2)、如果 $∠ A = 100^{\circ}$ ， $∠ C = 30^{\circ}$ ，求 $∠ B D E$ 的度数.

查看试题解析
23. 小亮步行上山游玩，设小亮出发 $x \min$ 后行走的路程为 $y m$ ，图中的折线表示小亮在整个行走过程中 $y$ 与 $x$ 的函数关系.

(1)、小亮行走的总路程是 $m$ ，他途中休息了 $\min$ .

(2)、当 $50 \leq x \leq 80$ 时，求 $y$ 与 $x$ 的函数关系式.

查看试题解析

五、解答题（三）（本大题共3小题，每小题8分，共24分）

24. 甲、乙两校参加区教育局举办的学生英语口语竞赛，两校参赛人数相等，比赛结束后，发现学生成绩分别为7分、8分、9分、10分（满分为10分），依据统计数据绘制了如下尚不完整的统计图表：

甲校成绩统计表

分数

7分

8分

9分

10分

人数

11

0

8

(1)、在扇形图中，“7分”所在扇形的圆心角等于度.

(2)、请你将条形统计图补充完整.

(3)、经统计，乙校的平均分是8.3分，中位数是8分，请写出甲校的平均分、中位数；并从平均分和中位数的角度分析哪个学校成绩较好.

(4)、如果该教育局要组织8人的代表队参加市级团体赛，为便于管理，决定从这两所学校中的一所挑选参赛选手，请你分析，应选哪所学校？

查看试题解析
25. 已知：直线 $y = \frac{3}{4} x + 6$ 与 $x$ 轴、 $y$ 轴分别相交于点A和点B，点C在线段AO上，将 $Δ A B O$ 沿 $B C$ 折叠后，点 $O$ 恰好落在AB边上点D处，如图.

(1)、直接写出点A和点B的坐标；

(2)、求AC的长；

(3)、点P为平面内一动点，且满足以 $A ， B ， C ， P$ 为顶点的四边形为平行四边形，请直接写出一个符合要求的 $P$ 点坐标.

查看试题解析

$x$	-1	0	1	2
$y$	-2	-1	0	$a$

年龄/岁	13	14	15	16
人数	1	1	2	1

	甲	乙	丙
$\bar{x}$	12.83秒	12.85秒	12.83
$s^{2}$	2.1	1.1	1.1

分数	7分	8分	9分	10分
人数	11	0		8