广东省惠州市四校2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-08-19 类型:期末考试
一、选择题(本大题10小题,每小题3分,共30分)在每小题列出的四个选项中,只有一个是正确的。
-
1. 下列二次根式,最简二次根式是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 下列各线段的长,能构成直角三角形的是A、2,3,4 B、5,12,13 C、4,6,9 D、5,11,134. 点 , 、 , 都在直线 上,且 则 、 的大小关系是A、 B、 C、 D、无法确定5. 一组数据3、2、4、5、2,则这组数据的众数是( )A、2 B、3 C、3.2 D、46. 下列命题中,真命题是A、两对角线相等的四边形是矩形 B、两对角线互相垂直的四边形是菱形 C、两对角线互相垂直平分且相等的四边形是正方形 D、一组对边相等另一组对边平行的四边形是平行四边形7. 如图,在四边形ABCD中,AB=CD,BC=AD,若∠D=120°,则∠C的度数为( )
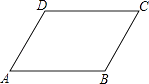 A、60° B、70° C、80° D、90°8. 已知直角三角形两条直角边长分别为5和12,则第三边上的中线长为A、5 B、6 C、6.5 D、129. 一次函数y=kx+k的图象可能是( )A、
A、60° B、70° C、80° D、90°8. 已知直角三角形两条直角边长分别为5和12,则第三边上的中线长为A、5 B、6 C、6.5 D、129. 一次函数y=kx+k的图象可能是( )A、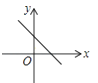 B、
B、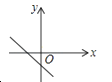 C、
C、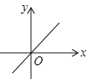 D、
D、 10. 甲、乙两人分别从A,B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min , 又各自按原速前往目的地,甲、乙两人之间的距离 与甲所用时间 之间的函数关系如图所示.有下列说法: ,B之间的距离为1200m; 乙行走的速度是甲的 倍; ; 以上结论正确的有
10. 甲、乙两人分别从A,B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min , 又各自按原速前往目的地,甲、乙两人之间的距离 与甲所用时间 之间的函数关系如图所示.有下列说法: ,B之间的距离为1200m; 乙行走的速度是甲的 倍; ; 以上结论正确的有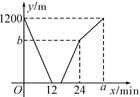 A、 B、 C、 D、①②③④
A、 B、 C、 D、①②③④二、填空题(本大题7小题,每小题4分,共28分)
-
11. 函数y= 的自变量取值范围是.12. 计算
 的结果等于. 13. 如图,函数y1=﹣2x和y2=ax+3的图象相交于点A(﹣1,m),则关于x的不等式﹣2x≥ax+的解集是.
的结果等于. 13. 如图,函数y1=﹣2x和y2=ax+3的图象相交于点A(﹣1,m),则关于x的不等式﹣2x≥ax+的解集是.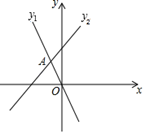 14. 已知菱形的两条对角线长分别是6和8,则这个菱形的面积为 .15. 一次函数y=2x-3与y=x+1的图象的交点坐标为 .16. 若一个直角三角形的三边分别为x , 4,5,则x= .17. 如图四边形ABCD , AD∥BC , AB⊥BC , AD=1,AB=2,BC=3,P为AB边上的一动点,以PD , PC为边作平行四边形PCQD , 则对角线PQ的长的最小值是.
14. 已知菱形的两条对角线长分别是6和8,则这个菱形的面积为 .15. 一次函数y=2x-3与y=x+1的图象的交点坐标为 .16. 若一个直角三角形的三边分别为x , 4,5,则x= .17. 如图四边形ABCD , AD∥BC , AB⊥BC , AD=1,AB=2,BC=3,P为AB边上的一动点,以PD , PC为边作平行四边形PCQD , 则对角线PQ的长的最小值是.
三、解答题(一)(本大题3小题,每小题6分,共18分)
-
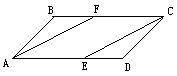
18.19. 如图,在▱ABCD中,已知点E和点F分别在AD和BC上,且DE=BF,连结CE和AF,试说明四边形AFCE是平行四边形.
 20. 一次函数图象经过(3,1),(2,0)两点.(1)、求这个一次函数的解析式;(2)、求当x=6时,y的值.
20. 一次函数图象经过(3,1),(2,0)两点.(1)、求这个一次函数的解析式;(2)、求当x=6时,y的值.四、解答题(二)(本大题3小题,每小题8分,共24分)
-
21. 在开展“学雷锋社会实践”活动中,某校为了解全校1000名学生参加活动的情况,随机调查了50名学生每人参加活动的次数,并根据数据绘成如图的条形统计图:
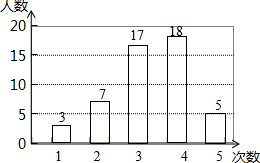 (1)、这50个样本数据的中位数是次,众数是次;(2)、求这50个样本数据的平均数;(3)、根据样本数据,估算该校1000名学生大约有多少人参加了4次实践活动.22. 如图,在菱形ABCD中,对角线AC与BD交于点O , 过点C作AC的垂线,过点D作BD的垂线,两直线相交于点E .
(1)、这50个样本数据的中位数是次,众数是次;(2)、求这50个样本数据的平均数;(3)、根据样本数据,估算该校1000名学生大约有多少人参加了4次实践活动.22. 如图,在菱形ABCD中,对角线AC与BD交于点O , 过点C作AC的垂线,过点D作BD的垂线,两直线相交于点E .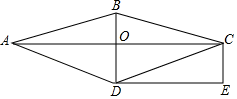 (1)、求证:四边形OCED是矩形;(2)、若CE=1, ,求四边形的ABCD面积.23. 某工厂计划生产A、B两种产品共50件,已知A产品成本2000元/件,售价2300元/件;B种产品成本3000元/件,售价3500元/件,设该厂每天生产A种产品x件,两种产品全部售出后共可获利y元.(1)、求出y与x的函数表达式;(2)、如果该厂每天最多投入成本140000元,那么该厂生产的两种产品全部售出后最多能获利多少元?
(1)、求证:四边形OCED是矩形;(2)、若CE=1, ,求四边形的ABCD面积.23. 某工厂计划生产A、B两种产品共50件,已知A产品成本2000元/件,售价2300元/件;B种产品成本3000元/件,售价3500元/件,设该厂每天生产A种产品x件,两种产品全部售出后共可获利y元.(1)、求出y与x的函数表达式;(2)、如果该厂每天最多投入成本140000元,那么该厂生产的两种产品全部售出后最多能获利多少元?五、解答题(三)(本大题2小题,每小题10分,共20分)
-
24. 如图,直线y=kx+6与x轴、y轴分别相交于点E、F , 点E的坐标为(﹣8,0),点A的坐标为(﹣6,0),点P是直线EF上的一个动点.
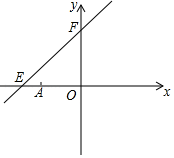 (1)、求k的值;(2)、点P在第二象限内的直线EF上的运动过程中,写出△OPA的面积S与x的函整表达式,并写出自变量x的取值范围;(3)、探究,当点P在直线EF上运动到时,△OPA的面积可能是15吗?若能,请求出点P的坐标;若不能,说明理由.25. 已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F , 垂足为O .
(1)、求k的值;(2)、点P在第二象限内的直线EF上的运动过程中,写出△OPA的面积S与x的函整表达式,并写出自变量x的取值范围;(3)、探究,当点P在直线EF上运动到时,△OPA的面积可能是15吗?若能,请求出点P的坐标;若不能,说明理由.25. 已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F , 垂足为O .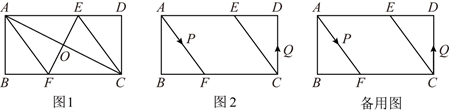 (1)、如图1,连接AF、CE,求证:四边形AFCE为菱形;(2)、如图1,求AF的长;(3)、如图2,动点P、Q分别从A、C两点同时出发,沿ΔAFB和ΔCDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,设运动时间为t秒.若点Q的速度为每秒0.8cm,当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.
(1)、如图1,连接AF、CE,求证:四边形AFCE为菱形;(2)、如图1,求AF的长;(3)、如图2,动点P、Q分别从A、C两点同时出发,沿ΔAFB和ΔCDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,设运动时间为t秒.若点Q的速度为每秒0.8cm,当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.