安徽省宿州市泗县2019-2020学年九年级上学期数学第一次月考试卷
试卷更新日期:2020-08-19 类型:月考试卷
一、单选题
-
1. 在下列方程中,是一元二次方程的有( )
① ;② ;③ ;④
A、1个 B、2个 C、3个 D、4个2. 利用求根公式求方程 的根时,a、b、c的值分别是( )A、 , , B、 , , C、 , , D、 , ,3. 习近平总书记提出了五年“精准扶贫”的战略构想,意味着每年要减贫约11700000人,将数据11700000用科学记数法表示为( )A、1.17×106 B、1.17×107 C、1.17×108 D、11.7×1064. 在四边形 中, ,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是( )A、 B、 C、 D、5. 一元二次方程 配方后化为( )A、 B、 C、 D、6. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、无解7. 根据下面表格中的对应值:x
3.23
3.24
3.25
3.26
ax2+bx+c
-0.06
-0.02
0.03
0.09
判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
A、3<x<3.23 B、3.23<x<3.24 C、3.24<x<3.25 D、3.25<x<3.268. 下列性质中菱形有矩形不一定具有的性质是( )A、对角线互相垂直 B、对角线互相平分 C、对角线相等 D、既是轴对称图形又是中心对称图形9. 一个菱形的边长是方程 的一个根,其中一条对角线长为8,则该菱形的面积为( )A、48 B、24 C、24或40 D、48或8010. 如图,在平面直角坐标系中,直线l为正比例函数 的图象,点 的坐标为 ,过点 作 轴的垂线交直线l于点 ,以 为边作正方形 ;过点 作直线l的垂线,垂足为 ,交x轴于点 ,以 为边作正方形 ;过点 作x轴的垂线,垂足为 ,交直线l于点 ,以 为边作正方形 ,…,按此规律操作下所得到的正方形 的面积是( )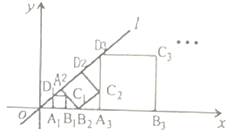 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
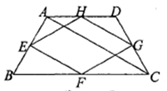
11. 以3和4为根的一元二次方程是 .12. 在实数范围内定义一种运算“ ”,其规则为 ,根据这个规则,方程 的解为 .13. 某花木场有一块如等腰梯形ABCD的空地(如图),各边的中点分别是E、F、G、H , 用篱笆围成的四边形EFGH场地的周长为40cm,则对角线 .
 14. 如图,在边长为6的正方形 中,点E是边 上一动点(不与A,B两点重合),过点E作 交对角线 于点F,连接 .当 是等腰三角形时, 的长度等于 .
14. 如图,在边长为6的正方形 中,点E是边 上一动点(不与A,B两点重合),过点E作 交对角线 于点F,连接 .当 是等腰三角形时, 的长度等于 .
三、解答题
-
15. 解方程: .16.
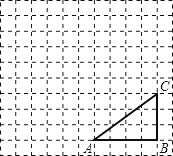
如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1 .
 (1)、在正方形网格中,作出△AB1C1;(不要求写作法)
(1)、在正方形网格中,作出△AB1C1;(不要求写作法)
(2)、设网格小正方形的边长为1cm,用阴影表示出旋转过程中线段BC所扫过的图形,然后求出它的面积.(结果保留π).
17. 如图, ,直线l分别交 、 于点A、C,同旁内角的平分线 、 相交于点B, 、 相交于点D.试证明四边形 是矩形.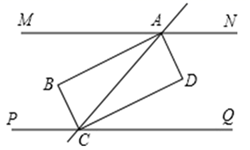 18. 关于x的一元二次方程 的实数解是 和 .(1)、求k的取值范围;(2)、如果 ,求k的值.19. 如图,四边形 为正方形, 的坐标 , 的从标 ,A、D在第一象限.
18. 关于x的一元二次方程 的实数解是 和 .(1)、求k的取值范围;(2)、如果 ,求k的值.19. 如图,四边形 为正方形, 的坐标 , 的从标 ,A、D在第一象限. (1)、过D作 轴,垂足为E,先证明 ,再写出点D的坐标;(2)、求点A的坐标.20. 先阅读,再解题
(1)、过D作 轴,垂足为E,先证明 ,再写出点D的坐标;(2)、求点A的坐标.20. 先阅读,再解题若某个一元二次方程的两根都是整数,且其中一根是另一根的整数倍,则称该方程是“倍根方程”.例如 的两根为 , ,因为 是 的-3倍,所以 是“倍根方程”.
(1)、说明 是“倍根方程”;(2)、已知关于x的一元二次方程 是“倍根方程”,其中m是整数,试探索m的取值条件.21. 如图,在矩形 中,对角线 的垂直平分线 分别交 、 、 于点E、O、F,连接 和 .E
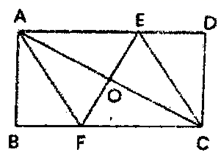 (1)、求证:四边形 为菱形.(2)、若 , ,求菱形 的周长.
(1)、求证:四边形 为菱形.(2)、若 , ,求菱形 的周长.