安徽省宿州市砀山县2019-2020学年九年级上学期数学12月月考试卷
试卷更新日期:2020-08-19 类型:月考试卷
一、单选题
-
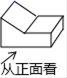
1. 一元二次方程3x2﹣x=0的解是( )A、x= B、x1=0,x2=3 C、x1=0,x2= D、x=02. 顺次连接矩形四边中点得到的四边形一定是( )A、正方形 B、矩形 C、菱形 D、平行四边形3. 如图所示,该几何体的左视图是( )
 A、
A、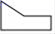 B、
B、 C、
C、 D、
D、 4. 某农场的粮食总产量为1500吨,设该农场人数为x人,平均每人占有粮食数为y吨,则y与x之间的函数图象大致是( )A、
4. 某农场的粮食总产量为1500吨,设该农场人数为x人,平均每人占有粮食数为y吨,则y与x之间的函数图象大致是( )A、 B、
B、 C、
C、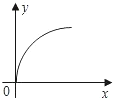 D、
D、 5. 小红上学要经过两个十字路口,每个路口遇到红、绿灯的机会都相同,小红希望上学时经过每个路口都是绿灯,但实际这样的机会是( )A、 B、 C、 D、6. 某机械厂七月份生产零件50万个,第三季度生产零件196万个.设该厂八、九月份平均每月的增长率为x,那么x满足的方程是( )A、50(1+x2)=196 B、50+50(1+x2)=196 C、50+50(1+x)+50(1+x)2=196 D、50+50(1+x)+50(1+2x)=1967. 当k>0时,反比例函数y= 和一次函数y=kx+2的图象大致是( )A、
5. 小红上学要经过两个十字路口,每个路口遇到红、绿灯的机会都相同,小红希望上学时经过每个路口都是绿灯,但实际这样的机会是( )A、 B、 C、 D、6. 某机械厂七月份生产零件50万个,第三季度生产零件196万个.设该厂八、九月份平均每月的增长率为x,那么x满足的方程是( )A、50(1+x2)=196 B、50+50(1+x2)=196 C、50+50(1+x)+50(1+x)2=196 D、50+50(1+x)+50(1+2x)=1967. 当k>0时,反比例函数y= 和一次函数y=kx+2的图象大致是( )A、 B、
B、 C、
C、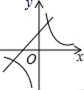 D、
D、 8. 对于反比例函数 ,下列说法错误的是A、图象分布在第二、四象限 B、当 时, 随 的增大而增大 C、图象经过点(1,-2) D、若点 , 都在图象上,且 ,则9. 如图,在△ABC中,AC=6,AB=4,点D,A在直线BC同侧,且∠ACD=∠ABC,CD=2,点E是线段BC延长线上的动点.若△DCE和△ABC相似,则线段CE的长为( )
8. 对于反比例函数 ,下列说法错误的是A、图象分布在第二、四象限 B、当 时, 随 的增大而增大 C、图象经过点(1,-2) D、若点 , 都在图象上,且 ,则9. 如图,在△ABC中,AC=6,AB=4,点D,A在直线BC同侧,且∠ACD=∠ABC,CD=2,点E是线段BC延长线上的动点.若△DCE和△ABC相似,则线段CE的长为( ) A、 B、 C、 或3 D、 或410. 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF= S△ABF . 其中正确的结论有( )个
A、 B、 C、 或3 D、 或410. 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF= S△ABF . 其中正确的结论有( )个 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
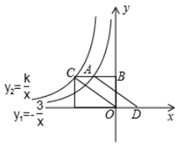
11. 已知 = ,则 的值是 .12. 袋子中有红球、白球共10个,这些球除颜色外都相同,将袋中的球搅匀,从中随机摸出一个球,记下颜色后再放回袋中,不断重复这一过程,摸了100次后,发现有33次摸到红球,请你估计这个袋中红球约有 个.13. 相邻两边长的比值是黄金分割数的矩形,叫做黄金矩形,从外形看,它最具美感.现在想要制作一张“黄金矩形”的贺年卡,如果较长的一条边长等于20厘米,那么相邻一条边的边长等于厘米.14. 反比例函数y1=- ,y2= 的图象如图所示,点A为y1=- 的图象上任意一点,过点A作x轴的平行线交y2= 的图象于点C,交y轴于点B.点D在x轴的正半轴上,CD∥OA.若四边形AODC的面积为2,则k的值为 .
三、解答题
-
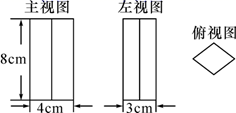
15. 解方程:2x2﹣1=3x.16. 一个几何体的三视图如图所示,它的俯视图为菱形.请写出该几何体的形状,并根据图中所给的数据求出它的侧面积.
 17. 如图,路灯( 点)距地面8米,身高1.6米的小明从距路灯的底部( 点 )20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了;变长或变短了多少米.
17. 如图,路灯( 点)距地面8米,身高1.6米的小明从距路灯的底部( 点 )20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了;变长或变短了多少米. 18. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1)、B(﹣3,2)、C(﹣1,4).
18. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1)、B(﹣3,2)、C(﹣1,4).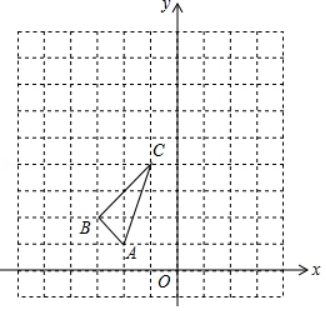 (1)、以原点O为位似中心,在第二象限内画出将△ABC放大为原来的2倍后的△A1B1C1 .(2)、画出△ABC绕C点逆时针旋转90°后得到的△A2B2C.19. 为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.(1)、小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?(2)、小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或;列表的方法进行说明.20. 如图,已知平行四边形 中,O是 的中点,连接 并延长,交 的延长线于点E.
(1)、以原点O为位似中心,在第二象限内画出将△ABC放大为原来的2倍后的△A1B1C1 .(2)、画出△ABC绕C点逆时针旋转90°后得到的△A2B2C.19. 为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.(1)、小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?(2)、小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或;列表的方法进行说明.20. 如图,已知平行四边形 中,O是 的中点,连接 并延长,交 的延长线于点E. (1)、求证: ;(2)、连接 , ,当 °时,四边形 是正方形?21. 某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高0.5元其销售量就减少10件,问:(1)、应将每件售价定为多少元时,才能使每天利润为640元?(2)、店主想要获得每天800元的利润,小红同学认为不可能,如果你同意小红同学的说法,请进行说明;如果你不同意,请简要说明理由.22. 如图,直线y=mx+n与双曲线y= 相交于A(﹣1,2)、B(2,b)两点,与y轴相交于点C.
(1)、求证: ;(2)、连接 , ,当 °时,四边形 是正方形?21. 某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高0.5元其销售量就减少10件,问:(1)、应将每件售价定为多少元时,才能使每天利润为640元?(2)、店主想要获得每天800元的利润,小红同学认为不可能,如果你同意小红同学的说法,请进行说明;如果你不同意,请简要说明理由.22. 如图,直线y=mx+n与双曲线y= 相交于A(﹣1,2)、B(2,b)两点,与y轴相交于点C.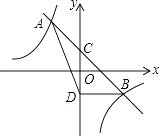 (1)、求m,n的值;(2)、若点D与点C关于x轴对称,求△ABD的面积;(3)、在坐标轴上是否存在异于D点的点P,使得S△PAB=S△DAB?若存在,直接写出P点坐标;若不存在,说明理由.23. 某班“手拉手”数学学习互助小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究时,遇到以下问题,请你逐一加以解答:
(1)、求m,n的值;(2)、若点D与点C关于x轴对称,求△ABD的面积;(3)、在坐标轴上是否存在异于D点的点P,使得S△PAB=S△DAB?若存在,直接写出P点坐标;若不存在,说明理由.23. 某班“手拉手”数学学习互助小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究时,遇到以下问题,请你逐一加以解答: (1)、如图1,正方形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H,则EFGH;(填“>”“=”或“<”)(2)、如图2,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H,求证: = ;(3)、如图3,四边形ABCD中,∠ABC=∠ADC=90°,BC=3,CD=5,AD=7.5,AM⊥DN,点M,N分别在边BC,AB上,求 的值.
(1)、如图1,正方形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H,则EFGH;(填“>”“=”或“<”)(2)、如图2,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H,求证: = ;(3)、如图3,四边形ABCD中,∠ABC=∠ADC=90°,BC=3,CD=5,AD=7.5,AM⊥DN,点M,N分别在边BC,AB上,求 的值.