安徽省芜湖市2019-2020学年九年级上学期数学10月月考试卷
试卷更新日期:2020-08-19 类型:月考试卷
一、单选题
-
1. 下列方程是一元二次方程的是( )A、 B、 C、 D、2. 一元二次方程 根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根3. 若m是方程 的一个根,则 的值为( )A、 B、 C、 D、4. 关于函数 的图象,下列叙述正确的是( )A、a的值越大,开口越大 B、a的值越小,开口越小 C、a的绝对值越大,开口越小 D、a的绝对值越小,开口越小5. 已知点 在抛物线 上,则 的大小关系是( )A、 B、 C、 D、6. 已知点 和点 (其中 )均在抛物线 上,则当 时,y值是( )A、 B、 C、 D、7. 下列选项中,能描述函数 与图象 的是( )A、
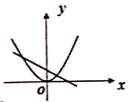 B、
B、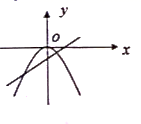 C、
C、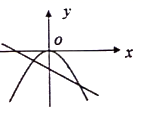 D、
D、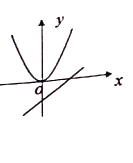 8. 已知x1、x2是关于x的方程x2﹣ax﹣2=0的两根,下列结论一定正确的是( )A、x1≠x2 B、x1+x2>0 C、x1•x2>0 D、x1<0,x2<09. 若 是方程 的一个根,设 则M与N的大小关系正确的为( )A、 B、 C、 D、不确定10. 如图所示,直线 与抛物线 交于 两点,且点A的横坐标是-2点 的横坐标是3则以下结论:
8. 已知x1、x2是关于x的方程x2﹣ax﹣2=0的两根,下列结论一定正确的是( )A、x1≠x2 B、x1+x2>0 C、x1•x2>0 D、x1<0,x2<09. 若 是方程 的一个根,设 则M与N的大小关系正确的为( )A、 B、 C、 D、不确定10. 如图所示,直线 与抛物线 交于 两点,且点A的横坐标是-2点 的横坐标是3则以下结论: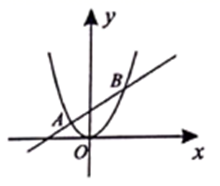
① 时,直线 与抛物线 的函数值都随着 的增大而增大;②AB的长度可以等于5;③ 有可能成为等边三角形;④当 时, 时,其中正确的结论是( )
A、①② B、①③ C、①④ D、②④二、填空题
-
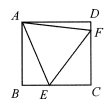
11. 若 则 .12. 若在抛物线 对称轴的左侧,y随x的增大而增大,则m= .13. 设直线 与抛物线 交于 两点,点p为直线 上方的抛物线 上一点,若 的面积为 ,则点p的坐标为 .14. 如图,在矩形ABCD中,点E,F分别在BC,CD边上,且CE=3,CF=4.若△AEF是等边三角形,则AB的长为.
 15. 已知x=2是关于x的一元二次方程kx2+(k2﹣2)x+2k+4=0的一个根,则k的值为 .
15. 已知x=2是关于x的一元二次方程kx2+(k2﹣2)x+2k+4=0的一个根,则k的值为 .三、解答题
-
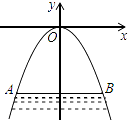
16. 解方程:17. 如图,某涵洞的截面是抛物线的一部分,现水面宽AB=1.6m,涵洞顶点O到水面的距离为2.4m,求涵洞所在抛物线的解析式.
 18. 某市特产大闸蟹,2016年的销售额是 亿元,因生态优质美誉度高,销售额逐年增加2018年的销售额达 亿元,若2017、2018年每年销售额增加的百分率都相同.(1)、求平均每年销售额增加的百分率;(2)、该市这3年大闸蟹的总销售额是多少亿元?19. 当行驶中的汽车撞到物体时,汽车的损坏程度通常用“撞击影响”来衡量.汽车的撞击影响I可以用汽车行驶速度v(km/min)来表示,下表是某种型号汽车的行驶速度与撞击影响的试验数据:
18. 某市特产大闸蟹,2016年的销售额是 亿元,因生态优质美誉度高,销售额逐年增加2018年的销售额达 亿元,若2017、2018年每年销售额增加的百分率都相同.(1)、求平均每年销售额增加的百分率;(2)、该市这3年大闸蟹的总销售额是多少亿元?19. 当行驶中的汽车撞到物体时,汽车的损坏程度通常用“撞击影响”来衡量.汽车的撞击影响I可以用汽车行驶速度v(km/min)来表示,下表是某种型号汽车的行驶速度与撞击影响的试验数据:v(km/min)
0
1
2
3
4
I
0
2
8
18
32
(1)、请根据上表中的数据,在直角坐标系中描出坐标(v,I)所对应的点,并用光滑曲线将各点连接起来;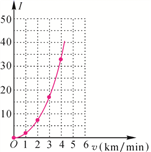 (2)、填写下表,并根据表中数据的呈现规律,猜想用v表示I的二次函数表达式;
(2)、填写下表,并根据表中数据的呈现规律,猜想用v表示I的二次函数表达式;v(km/min)
1
2
3
4
(3)、当汽车的速度分别是1.5 km/min , 2.5 km/min , 4.5 km/min时,利用你得到的撞击影响公式,计算撞击影响分别是多少?20. 已知关于x的一元二次方程 .(1)、当k取何值时,该方程有实数根?(2)、若等腰三角形一条边的边长为3它的另两条边的边长是这个方程的两个根,试求k的值.21. 如图,要在长、宽分别为50米、40米的矩形草坪内建一个正方形的观赏亭.为方便行人,分别从东,南,西,北四个方向修四条宽度相同的矩形小路与亭子相连,若小路的宽是正方形观赏亭边长的 ,小路与观赏亭的面积之和占草坪面积的 ,求小路的宽. 22. 温州某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元, 每增加1件,当天平均每件利润减少2元.设每天安排x人生产乙产品.(1)、根据信息填表:
22. 温州某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元, 每增加1件,当天平均每件利润减少2元.设每天安排x人生产乙产品.(1)、根据信息填表:产品种类
每天工人数(人)
每天产量(件)
每件产品可获利润(元)
甲
15
乙
x
x
(2)、若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.23. 如图所示,抛物线 与直线 交于两点 .已知点A坐标为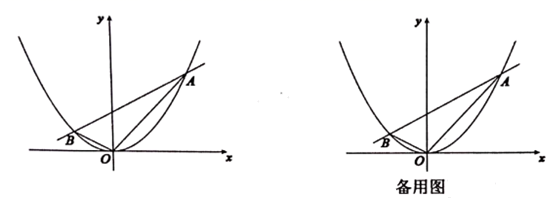 (1)、求B点坐标;(2)、求 的面积;(3)、将直线 从原点出发向上平移m个单位,设C为直线平移后其上一点,且满足 ,试求m的值.
(1)、求B点坐标;(2)、求 的面积;(3)、将直线 从原点出发向上平移m个单位,设C为直线平移后其上一点,且满足 ,试求m的值.