安徽省淮南市大通区2019-2020学年九年级上学期数学第一次月考试卷

试卷更新日期：2020-08-19 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列方程中，是一元二次方程的为（）

A、 $a x^{2} + b x + c = 0$ B、 $x^{2} + 3 x = 0$ C、 $\frac{1}{x^{2}} + \frac{1}{x} = 0$ D、 $x^{2} + 2 - x (x - 1) = 0$

查看试题解析
2. 若 $y = (2 - m) x^{m^{2} - 2}$ 是二次函数，则m的值为（）

A、2 B、-2 C、2或-2 D、0

查看试题解析
3. 二次函数 $y = - {(x + 2)}^{2} - 1$ 的顶点坐标为（）

A、 $(2, - 1)$ B、 $(2, 1)$ C、 $(- 2, 1)$ D、 $(- 2, - 1)$

查看试题解析
4. 一元二次方程 $x (x - 2) = x - 2$ 根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
5. 对于二次函数 $y = {(x - 3)}^{2} - 4$ 的图象，给出下列结论：①开口向上； ②对称轴是直线 $x = - 3$ ； ③顶点坐标是 $(3, - 4)$ ；④ $x > 3$ 时，y随x的增大而增大；⑤函数有最大值-4，其中正确的结论有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
6. 教育局组织学生篮球赛，有x支球队参加，每两队赛一场时，共需安排45场比赛，则正确的方程为（）

A、 $\frac{1}{2} x (x - 1) = 45$ B、 $\frac{1}{2} x (x + 1) = 45$ C、 $x (x - 1) = 45$ D、 $x (x + 1) = 45$

查看试题解析
7. 要得到二次函数 $y = x^{2} + 2 x - 2$ 的图象，需将 $y = x^{2}$ 的图象（）

A、向左平移1个单位，再向下平移3个单位 B、向右平移1个单位，再向上平移3个单位 C、向左平移1个单位，再向上平移3个单位 D、向右平移1个单位，再向下平移3个单位

查看试题解析
8. 已知二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，则一次函数 $y = a x + c$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
9. 某校办工厂生产的某种产品，今年产量为200件，计划通过改革技术，使今后两年的产量都比前一年增长一个相同的百分数，使得三年的总产量达到1 400件.若设这个百分数为x，则可列方程（）

A、 $200 + 200 {(1 + x)}^{2} = 1 400$ B、 $200 + 200 (1 + x) + 200 {(1 + x)}^{2} = 1 400$ C、 $200 {(1 + x)}^{2} = 1 400$ D、 $200 (1 + x) + 200 {(1 + x)}^{2} = 1 400$

查看试题解析
10. 二次函数y=ax²+bx+c的图象如图，点C在y轴的正半轴上，且OA=OC，则（）

A、ac+1=b B、ab+1=c C、bc+1=a D、以上都不是

查看试题解析

二、填空题

11. 如果a是一元二次方程x²-3x-3=0的一个解，那么代数式2a²-6a-8的值为．

查看试题解析
12. 如果抛物线 $y = a x^{2} + b x + c$ 经过 $(- 1, 0)$ 和 $(3, 0)$ ，那么对称轴是直线.

查看试题解析
13. 当 $x < 1$ 时，函数 $y = {(x - m)}^{2} - 2$ 的函数值y随着x的增大而减小，m的取值范围是．

查看试题解析
14. 已知二次函数的图象经过原点及点（-2，-2），且图象与x轴的另一个交点到原点的距离为4，那么该二次函数的解析式为

查看试题解析

三、解答题

15. 解方程： $x (2 x + 3) = 4 x + 6$

查看试题解析
16. 已知抛物线y=﹣2x²+4x+1．

(1)、求这个抛物线的对称轴和顶点坐标；

(2)、将这个抛物线平移，使顶点移到点P(－2，0)的位置，写出所得新抛物线的表达式和平移的过程．

查看试题解析
17. 如图所示，学校准备在教学楼后面搭建一简易矩形自行车车棚，一边利用教学楼的后墙（可利用的墙长为 $19 m$ ），另外三边利用学校现有总长 $36 m$ 的铁栏围成，留出2米长门供学生进出.若围成的面积为 $180 m^{2}$ ，试求出自行车车棚的长和宽.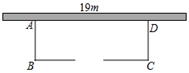

查看试题解析
18. 已知一个二次函数当 $x = 8$ 时，函数有最大值9，且图象过点 $(0, 1)$ .

(1)、求这个二次函数的关系式.

(2)、设 $A (6, y_{1})$ ， $B (8, y_{2})$ ， $C (10, y_{3})$ 是抛物线上的三点，直接写出 $y_{1}, y_{2}, y_{3}$ 的大小关系.

查看试题解析
19. 已知关于x的方程 $x^{2} + a x + a - 2 = 0$ .

(1)、当该方程的一个根为1时，求a的值及该方程的另一根；

(2)、求证：不论a取何实数，该方程都有两个不相等的实数根.

查看试题解析
20. 某市正大力发展绿色农产品，有一种有机水果A特别受欢迎，某超市以市场价格10元/千克在该市收购了6000千克A水果，立即将其冷藏，请根据下列信息解决问题：
①水果A的市场价格每天每千克上涨0.1元；

②平均每天有10千克的该水果损坏，不能出售；

③每天的冷藏费用为300元；

④该水果最多保存110天．

(1)、若将这批A水果存放 $x$ 天后一次性出售，则 $x$ 天后这批水果的销售单价为元；可以出售的完好水果还有千克；

(2)、将这批A水果存放多少天后一次性出售所得利润为9600元？

查看试题解析
21. 在一次篮球比赛中，如图队员甲正在投篮.已知球出手时离地面 $\frac{20}{9}$ m，与篮圈中心的水平距离为7 m，球出手后水平距离为4 m时达到最大高度4 m，设篮球运行轨迹为抛物线，篮圈距地面3 m.

(1)、建立如图所示的平面直角坐标系，问此球能否准确投中？

(2)、此时，对方队员乙在甲面前1 m处跳起盖帽拦截，已知乙的最大摸高为3.1 m，那么他能否获得成功？

查看试题解析
22. 如图，在 $Δ A B C$ 中， $∠ B = 90 °$ ， $A B = 5 c m$ ， $B C = 7 c m$ ，点P从点A开始沿 $A B$ 边向点B以 $1 c m / s$ 的速度移动，点Q从点B开始沿 $B C$ 边向点C以 $2 c m / s$ 的速度移动.

(1)、如果 $P ， Q$ 分别从 $A ， B$ 同时出发，那么几秒后， $Δ P B Q$ 的面积等于 $4 c m^{2}$ ？

(2)、如果 $P ， Q$ 分别从 $A ， B$ 同时出发， $Δ P B Q$ 的面积能否等于 $8 c m^{2}$ ？

(3)、如果 $P ， Q$ 分别从 $A ， B$ 同时出发，那么几秒后， $P Q$ 的长度等于 $5 c m$ ？

查看试题解析
23. 如图，已知抛物线 $y = - x + 2 x + 3$ 与 $x$ 轴交于A、B两点（点A在点B的左边），与y轴交于点C，连接 $B C$ .

(1)、求A、B、C三点的坐标；

(2)、若点P为线段 $B C$ 上的一点（不与B、C重合）， $P M / / y$ 轴，且 $P M$ 交抛物线于点M，交x轴于点N，当 $Δ B C M$ 的面积最大时，求 $Δ B P N$ 的周长.

查看试题解析