安徽省淮北市相山区2019-2020学年九年级上学期数学第三次月考试卷
试卷更新日期:2020-08-19 类型:月考试卷
一、单选题
-
1. 把抛物线y=﹣x2向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )A、y=﹣(x﹣1)2﹣3 B、y=﹣(x+1)2﹣3 C、y=﹣(x﹣1)2+3 D、y=﹣(x+1)2+32. 在△ABC中,∠A,∠B都是锐角,且sinA= , cosB= ,则△ABC是( )A、直角三角形 B、钝角三角形 C、锐角三角形 D、不能确定3. 如图,在 中, ,若 ,则 与 的面积之比是( )
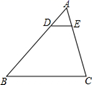 A、1:3 B、1:4 C、1:9 D、1:164. 若抛物线y=x2+2x+c的顶点在x轴上,则c的值为( )A、1 B、﹣1 C、2 D、45. 已知点(-1,y1),(2,y2),(3,y3)在反比例函数 的图象上.下列结论中正确的是( )A、y1>y2>y3 B、y1>y3>y2 C、y3>y1>y2 D、y2>y3>y16. 童装专卖店销售一种童装,已知这种童装每天所获得的利润y(元)与童装的销售单价x(元)之间满足关系式y=-x2+50x+500,则要想每天获得最大利润,单价需为( ).
A、1:3 B、1:4 C、1:9 D、1:164. 若抛物线y=x2+2x+c的顶点在x轴上,则c的值为( )A、1 B、﹣1 C、2 D、45. 已知点(-1,y1),(2,y2),(3,y3)在反比例函数 的图象上.下列结论中正确的是( )A、y1>y2>y3 B、y1>y3>y2 C、y3>y1>y2 D、y2>y3>y16. 童装专卖店销售一种童装,已知这种童装每天所获得的利润y(元)与童装的销售单价x(元)之间满足关系式y=-x2+50x+500,则要想每天获得最大利润,单价需为( ).
A、25元 B、20元 C、30元 D、40元7. 某水坝的坡度i=1: ,坡长AB=20米,则坝的高度为( )A、10米 B、20米 C、40米 D、208. 如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF:FC=( )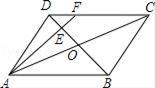 A、1:3 B、1:4 C、2:3 D、1:29. 已知二次函数的y=ax2+bx+c(a≠0)图象如图所示,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c<0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数),其中正确结论的个数有( )
A、1:3 B、1:4 C、2:3 D、1:29. 已知二次函数的y=ax2+bx+c(a≠0)图象如图所示,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c<0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数),其中正确结论的个数有( ) A、2 B、3 C、4 D、510. 如图所示,已知 中, 上的高 为BC上一点, ,交AB于点E , 交AC于点 不过A、 ,设E到BC的距离为x , 则 的面积y关于x的函数的图象大致为( ).
A、2 B、3 C、4 D、510. 如图所示,已知 中, 上的高 为BC上一点, ,交AB于点E , 交AC于点 不过A、 ,设E到BC的距离为x , 则 的面积y关于x的函数的图象大致为( ).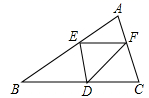 A、
A、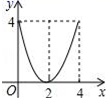 B、
B、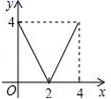 C、
C、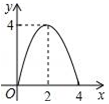 D、
D、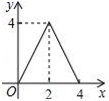
二、填空题
-
11. 若 ,则 = .12. AB是⊙O的直径,弦CD垂直平分半径OA,若CD长为6,则⊙O的半径长为 .
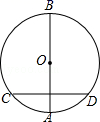 13. 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为 .
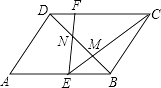
13. 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为 .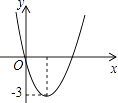 14. 如图,▱ABCD中,M、N是BD的三等分点,连接CM并延长交AB于点E,连接EN并延长交CD于点F,以下结论:
14. 如图,▱ABCD中,M、N是BD的三等分点,连接CM并延长交AB于点E,连接EN并延长交CD于点F,以下结论:①E为AB的中点;
②FC=4DF;
③S△ECF= ;
④当CE⊥BD时,△DFN是等腰三角形.
其中一定正确的是 .
 15. 计算tan260°﹣2sin30°﹣ cos45°的结果为 .
15. 计算tan260°﹣2sin30°﹣ cos45°的结果为 .三、解答题
-
16. 如图,一次函数 的图象与反比例函数 的图象交于点 、 .
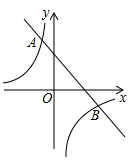 (1)、求反比例函数的解析式;(2)、当 时,直接写出x的取值范围.17. 如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC;
(1)、求反比例函数的解析式;(2)、当 时,直接写出x的取值范围.17. 如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC;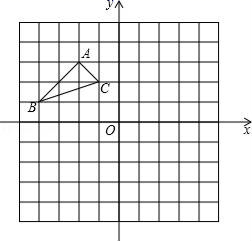 (1)、将△ABC向x轴正方向平移5个单位得△A1B1C1 ,(2)、再以O为旋转中心,将△A1B1C1旋转180°得△A2B2C2 , 画出平移和旋转后的图形,并标明对应字母.18. 已知 .(1)、求 的值;(2)、若 ,求x、y、z.19. 一船在A处测得北偏东45°方向有一灯塔B,船向正东方向以每小时20海里的速度航行1.5小时到达C处时,又观测到灯塔B在北偏东15°方向上,求此时航船与灯塔相距多少海里?
(1)、将△ABC向x轴正方向平移5个单位得△A1B1C1 ,(2)、再以O为旋转中心,将△A1B1C1旋转180°得△A2B2C2 , 画出平移和旋转后的图形,并标明对应字母.18. 已知 .(1)、求 的值;(2)、若 ,求x、y、z.19. 一船在A处测得北偏东45°方向有一灯塔B,船向正东方向以每小时20海里的速度航行1.5小时到达C处时,又观测到灯塔B在北偏东15°方向上,求此时航船与灯塔相距多少海里?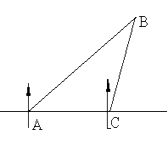 20. 已知:如图,D是BC上一点,△ABC∽△ADE,
20. 已知:如图,D是BC上一点,△ABC∽△ADE,
求证:∠1=∠2=∠3 .
21. 如图,已知矩形 的边长 .某一时刻,动点M从A点出发沿 方向以 的速度向B点匀速运动;同时,动点N从D点出发沿 方向以 的速度向A点匀速运动,问: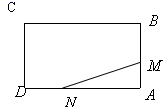 (1)、经过多少时间, 的面积等于矩形 面积的 ?(2)、是否存在时间t,使 的面积达到3.5cm2 , 若存在,求出时间t,若不存在,说明理由.22. 如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G
(1)、经过多少时间, 的面积等于矩形 面积的 ?(2)、是否存在时间t,使 的面积达到3.5cm2 , 若存在,求出时间t,若不存在,说明理由.22. 如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G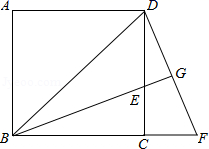 (1)、求证:△BDG∽△DEG;(2)、若EG•BG=4,求BE的长.23. 某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价为25元/件时,每天的销售量是150件;销售单价每上涨1元,每天的销售量就减少10件.(1)、求商场销售这种文具每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;(2)、求销售单价为多少元时,该文具每天的销售利润最大?(3)、现商场规定该文具每天销售量不少于120件,为使该文具每天的销售利润最大,该文具定价多少元时,每天利润最大?
(1)、求证:△BDG∽△DEG;(2)、若EG•BG=4,求BE的长.23. 某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价为25元/件时,每天的销售量是150件;销售单价每上涨1元,每天的销售量就减少10件.(1)、求商场销售这种文具每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;(2)、求销售单价为多少元时,该文具每天的销售利润最大?(3)、现商场规定该文具每天销售量不少于120件,为使该文具每天的销售利润最大,该文具定价多少元时,每天利润最大?