安徽省合肥市包河区2019-2020学年九年级上学期数学12月月考试卷

试卷更新日期：2020-08-19 类型：月考试卷

进入出卷网下载

一、单选题

1. 抛物线 $y = x^{2} - 3 x + 2$ 与 $y$ 轴交点的坐标是（）．

A、 $(0 ， 2)$ B、 $(1 ， 0)$ C、 $(0 ， - 3)$ D、 $(0 ， 0)$

查看试题解析
2. cos30°＝（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\sqrt{3}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
3. 观察下列每组图形，相似图形是（）

A、 B、 C、 D、

查看试题解析
4. 若反比例函数y= $\frac{k}{x}$ 图象经过点（5，-1），该函数图象在（）

A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限

查看试题解析
5. 对于二次函数 $y = - \frac{1}{4} x^{2} + x - 4$ ,下列说法正确的是（）

A、当x>0，y随x的增大而增大 B、当x=2时，y有最大值－3 C、图像的顶点坐标为（－2，－7） D、图像与x轴有两个交点

查看试题解析
6. 如图是二次函数 $y = a x^{2} + b x + c$ 的部分图象，由图象可知不等式 $a x^{2} + b x + c > 0$ 的解集是（）

A、 $x < - 1$ B、 $x > 5$ C、 $- 1 < x < 5$ D、 $x < - 1$ 或 $x > 5$

查看试题解析
7. 若 $△ A B C$ 的每条边长增加各自的 $10 %$ 得 $△ A' B' C'$ ,则 $∠ B'$ 的度数与其对应角 $∠ B$ 的度数相比（）

A、增加了 $10 %$ B、减少了 $10 %$ C、增加了 $(1 + 10 %)$ D、没有改变

查看试题解析
8. 如图，小正方形边长均为1，则下列图形中三角形(阴影部分)与△ABC相似的是（）

A、 B、 C、 D、

查看试题解析
9. 如果将抛物线 $y = a x^{2} + b x + c$ 向右平移2个单位,再向，上平移3个单位,得到新的抛物线 $y = {(x - 1)}^{2}$ ,那么（）

A、 $b = 6, c = 12$ B、 $b = - 6, c = 6$ C、 $b = 2, c = - 2$ D、 $b = 2, c = 4$

查看试题解析
10. 如图，在矩形 $A B C D$ 中，点 $H$ 为边 $B C$ 的中点，点G为线段 $D H$ .上的一点，且 $∠ B G C = 90 °$ ，延长 $B G$ 交 $C D$ 于点 $E$ ，延长 $C G$ 交 $A D$ 于点F，当 $C D = 4 ， D E = 1$ 时，则 $D F$ 的值为（）

A、2 B、 $\frac{3}{2}$ C、 $\frac{5}{2}$ D、 $\frac{9}{5}$

查看试题解析

二、填空题

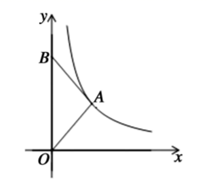
11. 对于锐角 $α, \tan α$ $\sin α$ ．（填 $" > ", " < " 或 " = "$ ）.

查看试题解析
12. 如图，在平面直角坐标系 $x O y$ 中，点B在y轴上， $A B = A O$ ，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过点a，若 $△ A B O$ 的面积为2，则k的值为. ．

查看试题解析
13. 如图， $D ， E$ 分别是 $△ A B C$ 的边上 $A B ， B C .$ 的点， $D E / / A C$ ，若 $S_{△ B D E} ： S_{△ C D E} = 1 ： 3$ ，当 $S_{△ D O E} = 1$ 时，则 $S_{△ A O C}$ 的值为= ．

查看试题解析
14. 在 $△ A B C$ 中，两条高 $A D ， C F$ 所在直线交与点 $H$ ，若 $\frac{C H}{A B} = \sqrt{3}$ ，则 $∠ A C B =$ ．

查看试题解析

三、解答题

15. 计算：
${(\frac{1}{2})}^{- 2} - {(π - 2018)}^{\circ} + 4 \sin 60^{\circ} \tan 60^{\circ}$

查看试题解析
16. 如图，在平面直角坐标系中，O为坐标原点，点N的坐标为（20，0），点M在第一象限内，且OM=10，sin∠MON= $\frac{3}{5}$ ．求：

(1)、点M的坐标；

(2)、cos∠MNO的值．

查看试题解析
17. 如图，在边长为 $1$ 的正方形网格中，已知 $A ， B ， C$ 三点的坐标分别是 $A (1 ， 0)$ ， $B (2 ， - 1) ， C (3 ， 1)$

(1)、请在网格图形中画出平面直角坐标系；

(2)、以原点O为位似中心，在网格中将 $△ A B C$ 放大2倍，画出放大后的 $△ A' B' C'$ ；

(3)、写出 $△ A' B' C'$ 各顶点的坐标： $A'$ ， $B'$ ； $C'$ ；

(4)、求 $△ A' B' C'$ 的的面积.

查看试题解析
18. 如图，在 $△ ABC$ 中， $A B = A C$ ，点E在边BC上移动（点E不与点B、C重合），满足 $∠ DEF = ∠ B$ ，且点D、F分别在边AB、AC上．

(1)、求证： $△ B D E \sim △ C E F$ ；

(2)、当点E移动到BC的中点时，求证：FE平分 $∠ DFC$ ．

查看试题解析
19. 应我市创建文明城市要求，某小区业主委员会决定把一块长 $80 m$ ，宽 $60 m$ 的矩形空地建成，花园小广场，设计方案如图所示，阴影区域为绿化区(四块绿化区为全等的直角三角形)，空白区域为活动区，且四周出口宽度一样，其宽度不小于 $36 m$ ，不大于 $44 m$ ，预计活动区造价 $60 元 / m^{2}$ ，绿化区造价 $50 元 / m^{2}$ ，设绿化区较长直角边为 $x m$ .

(1)、求工程队总造价y (元)与 $x (m)$ 的函数关系式，并求出x的取值范围；

(2)、如果业主委员会最多投资284万元，能否完成全部工程?若能，请写出x为整数的所有工程方案；若不能，请说明理由.

查看试题解析
20. 已知：如图，在平面直角坐标系 $x O y$ 中，直线 $A B$ 分别与x轴，y轴交于点 $B ， A$ ，与反比例函数的图象分别交于点 $C ， D ， C E ⊥ x$ 轴于点 $E ， t a n ∠ A B O = \frac{1}{2} ， O B = 4 ， O E = 2.$

(1)、求该反比例函数的解析式；

(2)、求 $△ C O E$ 的面积.

查看试题解析
21. 如图是某路灯在铅垂面内的示意图，灯柱 $B C$ 的高为 $10$ 米，灯柱 $B C$ 与灯杆 $A B$ 的夹角为 $120^{\circ}$ ，路灯采用锥形灯罩，在地面上的照射区域 $D E$ 的长为 $13$ 米，从 $D ， E$ 两处测得路灯A的仰角分别为 $α$ 和 $45^{\circ}$ ，且 $t a n α = 5. 5$ ，求灯杆 $A B$ 的长度.

查看试题解析
22. 如图，在锐角 $△ A B C$ 中， $B C = 8$ ，高 $A D = 6$ ，点 $E ， F$ 分别在 $A B ， A C$ 上，且 $E F / / B C ；$ 以 $E F$ 为边向下作正方形 $E F G H$ ，设正方形 $E F G H$ 与 $△ A B C$ 公共部分的面积为y，正方形 $E F G H$ 边长为x.

(1)、当 $H G$ 在 $B C$ 边上时，求正方形边长；

(2)、求y与x的函数关系式，并求出其最大值.

查看试题解析
23. 如图，矩形 $A B C D$ 中 $， A B = 16 ， B C = 12 ， E ， F$ 点在 $C D$ 边上，且 $c o s ∠ D A E = \frac{4}{5} ， H$ 是 $A B$ 边上的动点，射线 $H E$ 和射线 $A F$ 交于点G且 $∠ A G H = ∠ E A B .$

(1)、求 $D E$ 的长；

(2)、如果 $△ A H G$ 是以 $G H$ 为腰的等腰三角形，求线段 $A H$ 的长；

(3)、如果点F在线段 $C E$ 上(不与 $C ， E$ 重合)，设 $A H = x ， E F = y$ ，求y关于x的函数解析式.

查看试题解析