云南省红河州开远市2020年数学中考二模试卷
试卷更新日期:2020-08-18 类型:中考模拟
一、填空题
-
1. 的相反数是.2. 因式分解: .3. 函数 中自变量x的取值范围是.4. 如图,△ABC是等边三角形,沿图中的虚线剪去∠B,则∠1+∠2的度数等于.
 5. 用半径为6cm,圆心角为120°的扇形围成一个圆锥,则圆锥的底面圆半径为cm.6. 如图, 中, , ,将 绕点 逆时针旋转 ( )得 ,若 交 于点 ,当 时, 为等腰三角形.
5. 用半径为6cm,圆心角为120°的扇形围成一个圆锥,则圆锥的底面圆半径为cm.6. 如图, 中, , ,将 绕点 逆时针旋转 ( )得 ,若 交 于点 ,当 时, 为等腰三角形.
二、选择题
-
7. 我国民间,流传着许多含有吉祥意义的图案,表示对幸福生活的向往,良辰佳节的祝贺.比如下列图案分别表示“福”“禄”“寿”“喜”,其中是轴对称图形的有几个( )
 A、1个 B、2个 C、3个 D、4个8. 截止到3月26日0时,全球感染新型冠状病毒肺炎的人数已经突破380000人,“山川异域,风月同天”,携手抗“疫”,刻不容缓.将380000用科学记数法表示为( )A、0.38×106 B、3.8×106 C、3.8×105 D、38×1049. 下图是由几个相同的小正方形搭成的一个几何体,它的俯视图是( )
A、1个 B、2个 C、3个 D、4个8. 截止到3月26日0时,全球感染新型冠状病毒肺炎的人数已经突破380000人,“山川异域,风月同天”,携手抗“疫”,刻不容缓.将380000用科学记数法表示为( )A、0.38×106 B、3.8×106 C、3.8×105 D、38×1049. 下图是由几个相同的小正方形搭成的一个几何体,它的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 有11位同学参加学校举行的歌咏比赛,比赛后根据每个学生的最后得分计算出中位数、平均数、众数和方差,如果去掉一个最高分和一个最低分,则一定不会发生变化的是( )A、中位数 B、平均数 C、众数 D、方差11. 我国元朝数学家朱世杰的数学著作《四元玉鉴》中有一个“二果问价”问题,原题如下:“九百九十九文钱,甜果、苦果买一千,甜果九个十一文,苦果七个四文钱,试问甜苦果几个;”其大意为:用999文钱,可以买甜果和苦果共1000个,买9个甜果需要11文钱,买7个苦果需要4文钱,问买甜果和苦果的数量各多少个?设买甜果、苦果的数量分别为 个、 个,则可列方程组为( )A、 B、 C、 D、12. 若 ,则正比例函数 与反比例函数 在同一平面直角坐标系中的大致图象可能是( )A、
10. 有11位同学参加学校举行的歌咏比赛,比赛后根据每个学生的最后得分计算出中位数、平均数、众数和方差,如果去掉一个最高分和一个最低分,则一定不会发生变化的是( )A、中位数 B、平均数 C、众数 D、方差11. 我国元朝数学家朱世杰的数学著作《四元玉鉴》中有一个“二果问价”问题,原题如下:“九百九十九文钱,甜果、苦果买一千,甜果九个十一文,苦果七个四文钱,试问甜苦果几个;”其大意为:用999文钱,可以买甜果和苦果共1000个,买9个甜果需要11文钱,买7个苦果需要4文钱,问买甜果和苦果的数量各多少个?设买甜果、苦果的数量分别为 个、 个,则可列方程组为( )A、 B、 C、 D、12. 若 ,则正比例函数 与反比例函数 在同一平面直角坐标系中的大致图象可能是( )A、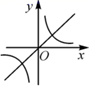 B、
B、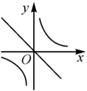 C、
C、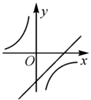 D、
D、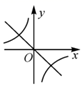 13. 如图,某建筑物的顶部有一块标识牌 CD,小明在斜坡上 B 处测得标识牌顶部C 的仰角为 45°, 沿斜坡走下来在地面 A 处测得标识牌底部 D 的仰角为 60°,已知斜坡 AB 的坡角为 30°,AB=AE=10 米.则标识牌 CD 的高度是( )米.
13. 如图,某建筑物的顶部有一块标识牌 CD,小明在斜坡上 B 处测得标识牌顶部C 的仰角为 45°, 沿斜坡走下来在地面 A 处测得标识牌底部 D 的仰角为 60°,已知斜坡 AB 的坡角为 30°,AB=AE=10 米.则标识牌 CD 的高度是( )米.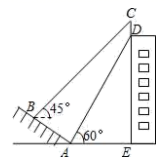 A、15-5 B、20-10 C、10-5 D、5 -514. 在科幻电影“银河护卫队”中,星球之间的穿梭往往靠宇宙飞船沿固定路径“空间跳跃”完成。如图所示:两个星球之间的路径只有 条,三个星球之间的路径有 条,四个星球之间的路径有 条,…,按此规律,则七个星球之间“空间跳跃”的路径有( )
A、15-5 B、20-10 C、10-5 D、5 -514. 在科幻电影“银河护卫队”中,星球之间的穿梭往往靠宇宙飞船沿固定路径“空间跳跃”完成。如图所示:两个星球之间的路径只有 条,三个星球之间的路径有 条,四个星球之间的路径有 条,…,按此规律,则七个星球之间“空间跳跃”的路径有( ) A、15条 B、21条 C、28条 D、32条
A、15条 B、21条 C、28条 D、32条三、解答题
-
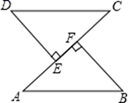
15. 先化简,再求值: ,其中 , .16. 已知:如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,AE=CF.求证:△ABF≌△CDE
 17. 某校积极开展“阳光体育”活动,并开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出).
17. 某校积极开展“阳光体育”活动,并开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出).
 (1)、求本次被调查的学生人数;(2)、补全条形统计图;(3)、在扇形统计图中,“篮球”部分所对应的圆心角度数为;(4)、该校共有3000名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?18. 某商场为了吸引顾客,设计了一种促销活动:在四等分的圆形转盘上依次标有“0元”、“10元”、“30元”、“50元”字样,购物每满300元可以转动转盘2次,每次转盘停下后,顾客可以获得指针所指区域相应金额的购物券(指针落在分界线上不计次数,需要再次转动转盘一次,直到指针没有落在分界线上),一个顾客刚好消费300元,并参加促销活动,转了2次转盘.(1)、请你用画树形图法或列表法,求出该顾客两次获得购物券金额和的所有可能结果;(2)、求出该顾客两次获得购物金额和不低于50元的概率.19. 已知二次函数 自变量 的值和它对应的函数值 如下表所示:
(1)、求本次被调查的学生人数;(2)、补全条形统计图;(3)、在扇形统计图中,“篮球”部分所对应的圆心角度数为;(4)、该校共有3000名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?18. 某商场为了吸引顾客,设计了一种促销活动:在四等分的圆形转盘上依次标有“0元”、“10元”、“30元”、“50元”字样,购物每满300元可以转动转盘2次,每次转盘停下后,顾客可以获得指针所指区域相应金额的购物券(指针落在分界线上不计次数,需要再次转动转盘一次,直到指针没有落在分界线上),一个顾客刚好消费300元,并参加促销活动,转了2次转盘.(1)、请你用画树形图法或列表法,求出该顾客两次获得购物券金额和的所有可能结果;(2)、求出该顾客两次获得购物金额和不低于50元的概率.19. 已知二次函数 自变量 的值和它对应的函数值 如下表所示:…
0
1
2
3
…
…
3
0
0
…
(1)、点M是该二次函数图象上一点,若点M纵坐标为8时,求点M的坐标;(2)、设该二次函数图象与 轴的左交点为 ,它的顶点为 ,该图象上点 的横坐标为4,求 的面积.20. 某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)、求甲、乙两种树苗每棵的价格各是多少元?
(2)、在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
21. 如图,在▱ABCD中,∠BAD的平分线交CD于点E,交BC的延长线于 点F,连接BE,∠F=45°. (1)、求证:四边形ABCD是矩形;(2)、若AB=14,DE=8,求sin∠AEB的值.22. 小雨、小华、小星暑假到某超市参加社会实践活动,在活动中他们参加了某种水果的销售工作,已知该水果的进价为8元 千克.他们通过市场调查发现:当销售单价为10元/千克时,那么每天可售出300千克;销售单价每上涨1元,每天的销售量就减少50千克.(1)、该超市销售这种水果,当销售单价不低于10元/千克时,请直接写出每天的销售量 (千克)与销售单价 (元 千克)之间的函数关系式;(2)、一段时间后,发现这种水果每天的销售量均不低于250千克,则此时该超市销售这种水果每天获取的利润 (元 最大是多少?23. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
(1)、求证:四边形ABCD是矩形;(2)、若AB=14,DE=8,求sin∠AEB的值.22. 小雨、小华、小星暑假到某超市参加社会实践活动,在活动中他们参加了某种水果的销售工作,已知该水果的进价为8元 千克.他们通过市场调查发现:当销售单价为10元/千克时,那么每天可售出300千克;销售单价每上涨1元,每天的销售量就减少50千克.(1)、该超市销售这种水果,当销售单价不低于10元/千克时,请直接写出每天的销售量 (千克)与销售单价 (元 千克)之间的函数关系式;(2)、一段时间后,发现这种水果每天的销售量均不低于250千克,则此时该超市销售这种水果每天获取的利润 (元 最大是多少?23. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE. (1)、求证:△ECF∽△GCE;(2)、求证:EG是⊙O的切线;(3)、延长AB交GE的延长线于点M,若tanG = ,AH=3 ,求EM的值.
(1)、求证:△ECF∽△GCE;(2)、求证:EG是⊙O的切线;(3)、延长AB交GE的延长线于点M,若tanG = ,AH=3 ,求EM的值.