陕西省铜川市新区2020年数学中考一模试卷
试卷更新日期:2020-08-18 类型:中考模拟
一、选择题
-
1. 计算:(﹣ )2﹣1=( )A、﹣ B、﹣ C、﹣ D、02. 如图,将直角三角形绕其一条直角边所在直线l旋转一周,得到的几何体是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 如图,∠B=40°,∠ACD=108°,若B,C,D三点在一条直线上,则∠A的大小是( )
3. 如图,∠B=40°,∠ACD=108°,若B,C,D三点在一条直线上,则∠A的大小是( )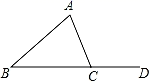 A、148° B、78° C、68° D、50°4. 对于正比例函数y=﹣3x,当自变量x的值增加1时,函数y的值增加( )A、﹣3 B、3 C、﹣ D、5. 计算(-2x2y)3的结果是( )A、-8x6y3 B、6x6y3 C、-8x5y3 D、-6x5y36. 如图, 在△ABC中,∠BAC=90°, AB=20, AC=15, △ABC的高AD与角平分线CF交于点E,则 的值为( )
A、148° B、78° C、68° D、50°4. 对于正比例函数y=﹣3x,当自变量x的值增加1时,函数y的值增加( )A、﹣3 B、3 C、﹣ D、5. 计算(-2x2y)3的结果是( )A、-8x6y3 B、6x6y3 C、-8x5y3 D、-6x5y36. 如图, 在△ABC中,∠BAC=90°, AB=20, AC=15, △ABC的高AD与角平分线CF交于点E,则 的值为( )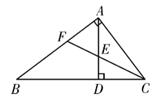 A、 B、 C、 D、7. 如图,已知直线l1:y=﹣2x+4与直线l2:y=kx+b(k≠0)在第一象限交于点M.若直线l2与x轴的交点为A(﹣2,0),则k的取值范围是( )
A、 B、 C、 D、7. 如图,已知直线l1:y=﹣2x+4与直线l2:y=kx+b(k≠0)在第一象限交于点M.若直线l2与x轴的交点为A(﹣2,0),则k的取值范围是( )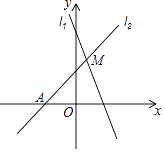 A、﹣2<k<2 B、﹣2<k<0 C、0<k<4 D、0<k<28. 如图,在矩形ABCD中,E为AD的中点,∠BED的平分线EF交BC于点F,若AB=6,BC=16,则FC的长度为( )
A、﹣2<k<2 B、﹣2<k<0 C、0<k<4 D、0<k<28. 如图,在矩形ABCD中,E为AD的中点,∠BED的平分线EF交BC于点F,若AB=6,BC=16,则FC的长度为( )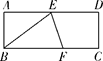 A、4 B、5 C、6 D、89. 如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为( )
A、4 B、5 C、6 D、89. 如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为( )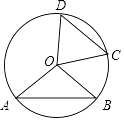 A、6 B、8 C、5 D、510. 已知二次函数 ( 为常数),当自变量 的值满足 时,与其对应的函数值 的最大值为-1,则 的值为( )
A、6 B、8 C、5 D、510. 已知二次函数 ( 为常数),当自变量 的值满足 时,与其对应的函数值 的最大值为-1,则 的值为( )
A、3或6 B、1或6 C、1或3 D、4或6二、填空题
-
11. 分解因式:x3﹣2x2+x= .12. 如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠CPD的度数是.
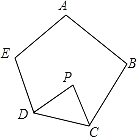 13. 如图,平面直角坐标系中,等腰 的顶点 分别在 轴、 轴的正半轴, 轴, 点 在函数 的图象上.若 则 的值为.
13. 如图,平面直角坐标系中,等腰 的顶点 分别在 轴、 轴的正半轴, 轴, 点 在函数 的图象上.若 则 的值为.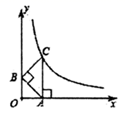 14. 如图,已知正方形ABCD中,AB=6,E是边AD的中点,P是边CD上的动点,Q是半圆BC上的动点,则PE+PQ的最小值是.
14. 如图,已知正方形ABCD中,AB=6,E是边AD的中点,P是边CD上的动点,Q是半圆BC上的动点,则PE+PQ的最小值是.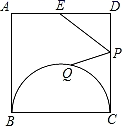
三、解答题
-
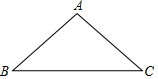
15. 计算: +(π﹣5)0﹣|2 ﹣3|.16. 解分式方程: + =1.17. 如图,已知△ABC,利用尺规在BC上找一点P,使得△ABP与△ACP均为直角三角形(不写作法,保留作图痕迹)
 18. 如图,在矩形ABCD中,E是AB的中点,连接DE、CE.
18. 如图,在矩形ABCD中,E是AB的中点,连接DE、CE.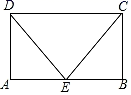
求证:△ADE≌△BCE.
19. 家访是学校与家庭沟通的有效渠道,是形成教育合力的关键,是转化后进生的催化剂.某市教育局组织全市中小学教师开展家访活动活动过程中,教育局随机抽取了部分教师调查其近两周家访次数,将采集到的数据按家访次数分成五类,并分别绘制了下面的两幅不完整的统计图.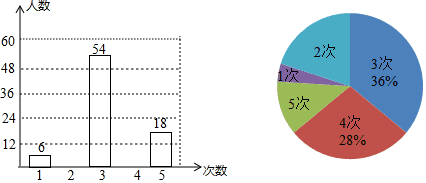
请根据以上信息,解答下列问题:
(1)、请把条形统计图补充完整;(2)、所抽取的教师中,近两周家访次数的众数是次,平均每位教师家访次;(3)、若该市有12000名教师,请估计近两周家访不少于3次的教师有多少名?20. 如图,小华和小康想用标杆来测量河对岸的树AB的高,两人在确保无安全隐患的情况下,小康在F处竖立了一根标杆EF,小华走到C处时,站立在C处看到标杆顶端E和树的顶端B在一条直线上,此时测得小华的眼睛到地面的距离DC=16米;然后,小华在C处蹲下,小康平移标杆到H处时,小华恰好看到标杆顶端G和树的顶端B在一条直线上,此时测得小华的眼睛到地面的距离MC=0.8米.已知EF=GH=2.4米,CF=2米,FH=1.6米,点C、F、H、A在一条直线上,点M在CD上,CD⊥AC,EF⊥AC,CH⊥AC,AB⊥AC,根据以上测量过程及测量数据,请你求出树AB的高度.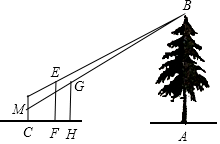 21. 油炸冰激凌是以面包、鸡蛋、冰激凌为材料制作的一种西式小吃,某油炸冰激凌专卖店每天固定制作甲、乙两个款型的油炸冰激凌共1000个,且所有产品当天全部售出,原料成本、销售单价及店员生产提成如表所示:
21. 油炸冰激凌是以面包、鸡蛋、冰激凌为材料制作的一种西式小吃,某油炸冰激凌专卖店每天固定制作甲、乙两个款型的油炸冰激凌共1000个,且所有产品当天全部售出,原料成本、销售单价及店员生产提成如表所示:甲(元/个)
乙(元/个)
原料成本
10
8
销售单价
20
16
生产提成
2
1.5
设该店每天制作甲款型的油炸冰激凌x个,每天获得的总利润为y元
(1)、求出y与x之间的函数关系式;(2)、若该店每天投入总成本不超过10750元,应怎样安排甲、乙两种款型的制作量,可使该店这一天所获得的利润最大?并求出最大利润(总成本=原料成本+生产提成,利润=销售收入﹣投入总成本)22. 某翻译团为成为2022年冬奥会志愿者做准备,该翻译团一共有五名翻译,其中一名只会翻译西班牙语,三名只会翻译英语,还有一名两种语言都会翻译.(1)、求从这五名翻译中随机挑选一名会翻译英语的概率;(2)、若从这五名翻译中随机挑选两名组成一组,请用树状图或列表的方法求该纽能够翻译上述两种语言的概率.23. 如图,已知AB是⊙O的直径,AC,BC是⊙O的弦,OE∥AC交BC于E,过点B作⊙O的切线交OE的延长线于点D,连接DC并延长交BA的延长线于点F.(1)、求证:DC是⊙O的切线;(2)、若∠ABC=30°,AB=8,求线段CF的长.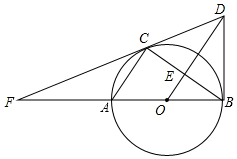 24. 已知抛物线L:y=x2+bx+c经过点M(2,﹣3),与y轴交于点C(0,﹣3).
24. 已知抛物线L:y=x2+bx+c经过点M(2,﹣3),与y轴交于点C(0,﹣3).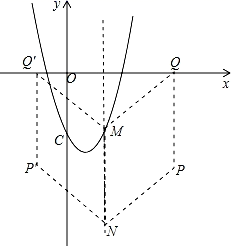 (1)、求抛物线L的表达式;(2)、试判断抛物线L与x轴交点的情况;(3)、平移该抛物线,设平移后的抛物线为L′,抛物线L′的顶点记为P,它的对称轴与x轴交于点Q,已知点N(2,﹣8),怎样平移才能使得以M、N、P、Q为顶点的四边形为菱形?25.
(1)、求抛物线L的表达式;(2)、试判断抛物线L与x轴交点的情况;(3)、平移该抛物线,设平移后的抛物线为L′,抛物线L′的顶点记为P,它的对称轴与x轴交于点Q,已知点N(2,﹣8),怎样平移才能使得以M、N、P、Q为顶点的四边形为菱形?25.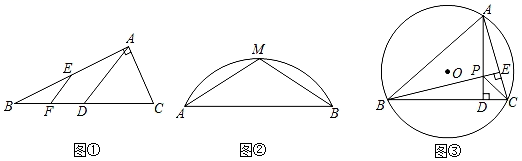 (1)、问题提出:
(1)、问题提出:如图①,在Rt△BAC中,∠BAC=90°,点D,E分别是CB,AB的中点,点F是BD的中点,若AB=8,AC=6,则EF=;
(2)、问题探究:如图②,已知:M是弓形AB上的中点,AB=24,弓形AB的高是8,则对应⊙O的面积为多少?(结果保留根号或π)
(3)、问题解决:如图③,在半径为5的⊙O中,弦BC=8,点A为优弧BC上的动点,过点A作AD⊥BC于点D,过点B作BE⊥AC于点E.AD和BE交于点P,连接PC,试求△PBC面积的最大值.