辽宁省营口市2020年数学中考模拟试卷（6月）

试卷更新日期：2020-08-18 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列各数中是有理数的是(　　)

A、 $\sqrt[]{2020}$ B、- $\frac{1}{2020}$ C、- $\sqrt[]{2020}$ D、π

查看试题解析
2. 下列几何体中，主视图与俯视图不相同的是（）

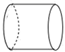
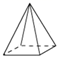
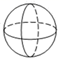A、正方体 B、圆柱 C、四棱锥 D、球

查看试题解析
3. 下列运算正确的是（　　）

A、2a+3b＝5ab B、2（2a﹣b）＝4a﹣b C、（a+b）（a﹣b）＝a²﹣b² D、（a+b）²＝a²+b²

查看试题解析
4. 如图，直线a∥b，点B在直线b上，且AB⊥BC，∠1＝57°，则∠2的度数是（　　）

A、43° B、33° C、53° D、123°

查看试题解析
5. 某小组5名同学在一周内参加家务劳动的时间如表所示，关于“劳动时间”的这组数据，以下说法正确的是（）
动时间（小时）
3
3.5
4
4.5
人数
1
1
2
1

A、中位数是4，平均数是3.75 B、众数是4，平均数是3.75 C、中位数是4，平均数是3.8 D、众数是2，平均数是3.8

查看试题解析
6. 如图，AB是⊙O的直径，弦CD⊥AB于点E，OC=5cm，CD=8cm，则AE=（）

A、8cm B、5cm C、3cm D、2cm

查看试题解析
7. 为庆祝建国70周年，某校决定组织全校600名师生参观“建国70年成就展”，租用10辆大客车和8辆小客车，恰好全部坐满已知每辆大客车的座位数比小客车多15个.若设每辆大客车有x个座位，每辆小客车有y个座位，则可列方程组为（　　）

A、 ${\begin{array}{l} 10 x + 8 y = 600 \\ x = 15 - y \end{array}$ B、 ${\begin{array}{l} 10 x + 8 y = 600 \\ x + y = 15 \end{array}$ C、 ${\begin{array}{l} 10 x + 8 y = 600 \\ y - x = 15 \end{array}$ D、 ${\begin{array}{l} 10 x + 8 y = 600 \\ x - y = 15 \end{array}$

查看试题解析
8.
如图，将边长为2的正方形铁丝框ABCD，变形为以A为圆心，AB为半径的扇形（忽略铁丝的粗细），则所得的扇形ADB的面积为（　　）

A、3 B、4 C、6 D、8

查看试题解析
9. 如图，在△ABC中，∠ACB=90°，AC=BC=1，E、F为线段AB上两动点，且∠ECF=45°，过点E、F分别作BC、AC的垂线相交于点M，垂足分别为H、G.现有以下结论：①AB= $\sqrt{2}$ ；②AF+BE=EF；③当点E与点B重合时，MH= $\frac{1}{2}$ ；其中正确结论的个数是(　　)

A、0 B、1 C、2 D、3

查看试题解析
10. 抛物线y=ax²+bx+c的对称轴为直线x=﹣1，部分图象如图所示，下列判断中：①abc＞0；②b²﹣4ac＞0；③9a﹣3b+c=0；④若点( $- \frac{1}{2}$ ，y₁)，(﹣2，y₂)均在抛物线上，则y₁＞y₂；⑤5a﹣2b＜0；其中正确的个数有(　　)

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

11. 在函数 $y = \frac{\sqrt{x}}{x - 1}$ 中，自变量x的取值范围是.

查看试题解析
12. 习总书记提出“一带一路”的伟大构想以后，上海仅2015年12月对“一带一路”沿线国家和地区的投资就达到了92亿美元，其中92亿美元用科学记数法表示为美元.

查看试题解析
13. 关于x的一元二次方程kx²﹣x+1=0有实数根，则k的取值范围是．

查看试题解析
14. 因式分解： $2 x^{2} - 8 =$ .

查看试题解析
15. 有4根细木棒，长度分别为2cm、3cm、4cm、5cm，从中任选3根，恰好能搭成一个三角形的概率是．

查看试题解析
16. 如图，直角三角形的直角顶点在坐标原点， $∠ O A B = 30 °$ ，若点 $A$ 在反比例函数 $y = \frac{6}{x} (x > 0)$ 的图象上，则经过点 $B$ 的反比例函数解析式为；

查看试题解析
17. 如图，已知在Rt△ABC中，∠C＝90°，AC＝18.分别以A、B为圆心，大于 $\frac{1}{2}$ AB长为半径作弧，过弧的交点作直线，分别交AB、AC于点D、E.若EC＝5，则△BEC的面积为.

查看试题解析
18. 如图，直线y=﹣ $\frac{\sqrt{3}}{3}$ x+2与x轴y轴分别交于A、C两点，以AC为对角线作第一个矩形ABCO，对角线交点为A₁ ，再以CA₁为对角线作第二个矩形A₁B₁CO₁ ，对角线交点为A₂ ，同法作第三个矩形A₂B₂CO₂对角线交点为A₃ ， …以此类推，则第2020个矩形对角线交点A₂₀₂₀的坐标为.

查看试题解析

三、解答题

19. 先化简，再求值： $(\frac{1}{x + 4} + \frac{1}{x - 4}) \div \frac{1}{x^{2} - 16}$ ，其中x＝ $\sqrt{2} - 1$ ．

查看试题解析
20. 为了丰富居民的文化生活.某社区开展跳舞、绘画、游泳、唱歌等活动来让居民娱乐.为了解居民对跳舞、绘画、游泳、唱歌这四种活动(以下分别用 $A$ ， $B$ ， $C$ ， $D$ 表示这四种不同活动)的喜爱情况，在“五一”劳动节期间对某居民区市民进行了抽样调查，并将调查结果绘制成如下两幅统计图.请根据以上信息回答：

(1)、本次参加抽样调查的居民有多少人？

(2)、将不完整的条形图补充完整；

(3)、若居民区有8000人，请估计爱唱歌的人数？

查看试题解析
21. 小明家客厅里装有一种三位单极开关，分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯，按下任意一个开关均可打开对应的一盏电灯，因刚搬进新房不久，不熟悉情况.

(1)、若小明任意按下一个开关，则小明打开走廊灯的概率是多少？

(2)、若任意按下一个开关后，再按下另两个开关中的一个，则正好客厅灯和走廊灯同时亮的概率是多少？请用树状图法或列表法加以说明.

查看试题解析
22. 如图，在一笔直的海岸线上有A、B两上观测站，A在B的正东方向，BP＝6 $\sqrt{2}$ （单位：km）．有一艘小船停在点P处，从A测得小船在北偏西60°的方向，从B测得小船在北偏东45°的方向．

(1)、求A、B两观测站之间的距离；

(2)、小船从点P处沿射线AP的方向进行沿途考察，求观测站B到射线AP的最短距离．

查看试题解析
23. 如图，已知⊙A与菱形ABCD的边BC相切于点E，与边AB相交于点F，连接EF.

(1)、求证：CD是⊙A的切线；

(2)、若⊙A的半径为2，tan∠BEF＝ $\frac{\sqrt{3}}{3}$ ，求图中阴影部分的面积.

查看试题解析
24. 某工厂制作 $A, B$ 两种手工艺品， $B$ 每天每件获利比 $A$ 多105元，获利30元的 $A$ 与获利240元的 $B$ 数量相等．

(1)、制作一件 $A$ 和一件 $B$ 分别获利多少元？

(2)、工厂安排65人制作 $A$ ， $B$ 两种手工艺品，每人每天制作2件 $A$ 或1件 $B$ ．现在在不增加工人的情况下，增加制作 $C$ ．已知每人每天可制作1件 $C$ （每人每天只能制作一种手工艺品），要求每天制作 $A$ ， $C$ 两种手工艺品的数量相等．设每天安排 $x$ 人制作 $B$ ， $y$ 人制作 $A$ ，写出 $y$ 与 $x$ 之间的函数关系式．

(3)、在（1）（2）的条件下，每天制作 $B$ 不少于5件．当每天制作5件时，每件获利不变．若每增加1件，则当天平均每件获利减少2元．已知 $C$ 每件获利30元，求每天制作三种手工艺品可获得的总利润 $W$ （元）的最大值及相应 $x$ 的值．

查看试题解析
25. 如图，AM是△ABC的中线，D是线段AM上一点（不与点A重合）.DE∥AB交AC于点F，CE∥AM，连结AE.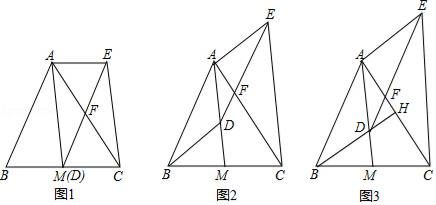

(1)、如图1，当点D与M重合时，求证：四边形ABDE是平行四边形；

(2)、如图2，当点D不与M重合时，（1）中的结论还成立吗？请说明理由.

(3)、如图3，延长BD交AC于点H，若BH⊥AC，且BH=AM.
①求∠CAM的度数；

②当FH= $\sqrt{3}$ ，DM=4时，求DH的长.

查看试题解析
26. 如图，在平面直角坐标系中，抛物线 $y = \frac{1}{2} x^{2} - \frac{1}{2} x$ 上有两点 $A$ ， $B$ ，连接 $O A$ ， $O B$ ， $A B$ ，直线 $A B$ 交 $y$ 轴于点 $C$ ，点 $A$ 到两坐标轴的距离相等.点 $B$ 到两坐标轴的距离也相等.

(1)、求点 $A$ ， $B$ 的坐标并直接写出 $△ O A B$ 的形状；

(2)、若点 $P$ 为线段 $O B$ 上的一个动点（不与点 $O$ ， $B$ 重合），连接 $P C$ ，当 $△ O P C$ 为等腰三角形时，求点 $P$ 的坐标；

(3)、若点 $F$ 为 $x$ 轴上一动点，当 $△ F A B$ 是以 $A B$ 为斜边的直角三角形时，求点 $F$ 的坐标.

查看试题解析

动时间（小时）	3	3.5	4	4.5
人数	1	1	2	1