江苏省无锡市凤翔集团2020年数学中考一模试卷
试卷更新日期:2020-08-18 类型:中考模拟
一、选择题
-
1. -5的相反数是( )A、-5 B、5 C、 D、2. 使 有意义的x的取值范围是( )
A、x≤3 B、x<3 C、x≥3 D、x>33. 下列计算正确的是( )A、 B、 C、 D、4. 有6个相同的立方体搭成的几何体如图所示,则它的主视图是( )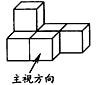 A、
A、 B、
B、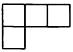 C、
C、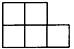 D、
D、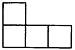 5. 用两块大小相同的含30°角的三角板拼成的四边形中,轴对称图形有( )
5. 用两块大小相同的含30°角的三角板拼成的四边形中,轴对称图形有( ) A、1个 B、2个 C、3个 D、4个6. 下列性质中,矩形具有而菱形不一定具有的是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、邻边相等7. 如图,BD∥AC,BE平分∠ABD,交AC于点E.若∠A=50°,则∠1的度数为( )
A、1个 B、2个 C、3个 D、4个6. 下列性质中,矩形具有而菱形不一定具有的是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、邻边相等7. 如图,BD∥AC,BE平分∠ABD,交AC于点E.若∠A=50°,则∠1的度数为( )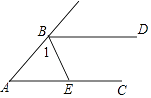 A、65° B、60° C、55° D、50°8. 一个不透明的口袋中有6个白球和12个黑球,“任意摸出n个球,其中至少有一个白球”是必然事件,n等于( )A、6 B、7 C、13 D、189. 方程 的正根的个数为( )A、0个 B、1个 C、2个 D、3个10. 如图,正方形 中, , 是 中点, 上有一动点 ,连接 、 ,将 沿着 翻折得到 .连接 、 ,则 的最小值为( )
A、65° B、60° C、55° D、50°8. 一个不透明的口袋中有6个白球和12个黑球,“任意摸出n个球,其中至少有一个白球”是必然事件,n等于( )A、6 B、7 C、13 D、189. 方程 的正根的个数为( )A、0个 B、1个 C、2个 D、3个10. 如图,正方形 中, , 是 中点, 上有一动点 ,连接 、 ,将 沿着 翻折得到 .连接 、 ,则 的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 一元二次方程x2=3x的解是: .12. 若 = ,则 的值为 .13. 绿水青山就是金山银山,为了创造良好的生态生活环境,我省2017年清理河湖库塘淤泥约为116000000方,数字116000000用科学记数法可以表示为.14. 小明的爸爸是个“健步走”运动爱好者,他用手机软件记录了某个月(30天)每天健步走的步数,并将记录结果绘制成了如下统计表:
步数(万步)
1.1
1.2
1.3
1.4
1.5
天数
3
7
5
12
3
在每天所走的步数这组数据中,中位数是(万步).
15. 若一个圆锥的侧面展开图是一个半径为 ,圆心角为120°的扇形,则该圆锥的底面半径为 .16. 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上, ,顶点C的坐标为 ,x反比例函数 的图象与菱形对角线AO交于点D,连接BD,当 轴时,k的值是. 17. 如图,△ABC中,D为BC上一点,∠BAD=∠C,AB=6,BD=4,则CD的长为 .
17. 如图,△ABC中,D为BC上一点,∠BAD=∠C,AB=6,BD=4,则CD的长为 .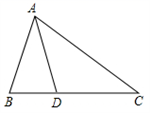 18. 如图,在平面直角坐标系中, 的顶点坐标分别为 , , ,点 绕点A旋转180°得到点 ,点 绕点B旋转180°得到点 ,点 绕点C旋转180°得到点 ,点 绕点A旋转180°得到点 , ,按此作法进行下去,则点P2019的坐标为.
18. 如图,在平面直角坐标系中, 的顶点坐标分别为 , , ,点 绕点A旋转180°得到点 ,点 绕点B旋转180°得到点 ,点 绕点C旋转180°得到点 ,点 绕点A旋转180°得到点 , ,按此作法进行下去,则点P2019的坐标为.
三、解答题
-
19. 计算或化简:(1)、(2)、20. 解方程和不等式(组):(1)、;(2)、.21. 如图, 是平行四边形 的一条对角线, 于点 , 于点 ,求证: .
 22. 近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.
22. 近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)、本次一共调查了多少名购买者?
(2)、请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为度.(3)、若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
23. 某天,甲、乙、丙三人一起乘坐公交车,他们上车时发现公交车上还有 , , 三个空座位,且只有 , 两个座位相邻,若三人随机选择座位,试解决以下问题:(1)、甲选择座位 的概率是;(2)、试用列表或画树状图的方法,并求甲、乙选择相邻座位 , 的概率.24. 如图,直线 与 相交于点 , , 是 上两点,点 是直线 上的点,且 ,请利用圆规和无刻度直尺在图中作出符合条件的点 . 25. 如图1,Rt△ABC中,∠C=90°,AB=15,BC=9,点D,E分别在AC,BC上,CD=4 x,CE=3x,其中0<x<3.
25. 如图1,Rt△ABC中,∠C=90°,AB=15,BC=9,点D,E分别在AC,BC上,CD=4 x,CE=3x,其中0<x<3.
 (1)、求证:DE∥AB;(2)、当x=1时 ,求点E到AB的距离;(3)、将△DCE绕点E逆时针方向旋转,使得点D落在AB边上的D′处. 在旋转的过程中,若点D′的位置有且只有一个,求x的取值范围.26. 某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额﹣生产费用)
(1)、求证:DE∥AB;(2)、当x=1时 ,求点E到AB的距离;(3)、将△DCE绕点E逆时针方向旋转,使得点D落在AB边上的D′处. 在旋转的过程中,若点D′的位置有且只有一个,求x的取值范围.26. 某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额﹣生产费用)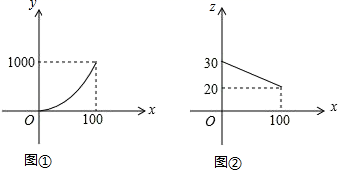 (1)、请直接写出y与x以及z与x之间的函数关系式;(2)、求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?(3)、由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?27. 如图, 与 轴交于点C,与 轴的正半轴交于点K,过点 作 轴交抛物线于另一点B,点 在 轴的负半轴上,连结 交 轴于点A,若 .
(1)、请直接写出y与x以及z与x之间的函数关系式;(2)、求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?(3)、由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?27. 如图, 与 轴交于点C,与 轴的正半轴交于点K,过点 作 轴交抛物线于另一点B,点 在 轴的负半轴上,连结 交 轴于点A,若 . (1)、用含 的代数式表示 的长;(2)、当 时,判断点 是否落在抛物线上,并说明理由;(3)、过点 作 轴交 轴于点 延长 至 ,使得 连结 交 轴于点 连结AE交 轴于点 若 的面积与 的面积之比为 则求出抛物线的解析式.28. 如图(1),在平面直角坐标系中,点 ,点 ,点 从点 出发,沿 以1个单位每秒的速度匀速运动,同时点 从点 出发,沿 轴正方向以2个单位每秒的速度匀速运动. ,交 于点 ,交 轴于点 .当点 到达点 时,两点同时停止运动,设运动的时间为 秒.在整个运动过程中,设 与 的重叠部分的面积为 .
(1)、用含 的代数式表示 的长;(2)、当 时,判断点 是否落在抛物线上,并说明理由;(3)、过点 作 轴交 轴于点 延长 至 ,使得 连结 交 轴于点 连结AE交 轴于点 若 的面积与 的面积之比为 则求出抛物线的解析式.28. 如图(1),在平面直角坐标系中,点 ,点 ,点 从点 出发,沿 以1个单位每秒的速度匀速运动,同时点 从点 出发,沿 轴正方向以2个单位每秒的速度匀速运动. ,交 于点 ,交 轴于点 .当点 到达点 时,两点同时停止运动,设运动的时间为 秒.在整个运动过程中,设 与 的重叠部分的面积为 . (1)、求当 为何值时,点 与点 、 在同一直线上;(2)、求 关于 的函数关系式;(3)、在图(3)中画出 关于 的函数图象,直接写出 的最大值.
(1)、求当 为何值时,点 与点 、 在同一直线上;(2)、求 关于 的函数关系式;(3)、在图(3)中画出 关于 的函数图象,直接写出 的最大值.